SERA POOLS Study
Model 1 Results
R. Noah Padgett
2022-02-01
Last updated: 2022-02-02
Checks: 4 2
Knit directory: Padgett-Dissertation/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20210401) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
- model1
To ensure reproducibility of the results, delete the cache directory pools_model1_results_cache and re-run the analysis. To have workflowr automatically delete the cache directory prior to building the file, set delete_cache = TRUE when running wflow_build() or wflow_publish().
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Tracking code development and connecting the code version to the results is critical for reproducibility. To start using Git, open the Terminal and type git init in your project directory.
This project is not being versioned with Git. To obtain the full reproducibility benefits of using workflowr, please see ?wflow_start.
# Load packages & utility functions
source("code/load_packages.R")
source("code/load_utility_functions.R")
# environment options
options(scipen = 999, digits=3)POOLS Data
library(readxl)
mydata <- read_excel("data/pools/POOLS_data_2020-11-16.xlsx")
use.var <- c(paste0("Q4_",c(3:5,9,11,15,18)),
paste0("Q5_",c(1:3,5:6,12)),
paste0("Q6_",c(2,5:8, 11)),
paste0("Q7_",c(2, 4:5, 7:8, 14)))
# trichotomize
f <- function(x){
y=numeric(length(x))
for(i in 1:length(x)){
if(x[i] < 3){
y[i] = 1
}
if(x[i] == 3){
y[i] = 2
}
if(x[i] > 3){
y[i] = 3
}
}
return(y)
}
mydata <- na.omit(mydata[, use.var])
mydata <- apply(mydata, 2, f) %>%
as.data.frame()
psych::describe(
mydata
) vars n mean sd median trimmed mad min max range skew kurtosis se
Q4_3 1 490 1.62 0.65 2 1.53 1.48 1 3 2 0.57 -0.68 0.03
Q4_4 2 490 1.64 0.65 2 1.56 1.48 1 3 2 0.51 -0.71 0.03
Q4_5 3 490 1.52 0.68 1 1.40 0.00 1 3 2 0.92 -0.36 0.03
Q4_9 4 490 1.65 0.76 1 1.56 0.00 1 3 2 0.69 -0.96 0.03
Q4_11 5 490 1.64 0.72 1 1.55 0.00 1 3 2 0.66 -0.85 0.03
Q4_15 6 490 1.58 0.68 1 1.47 0.00 1 3 2 0.74 -0.59 0.03
Q4_18 7 490 1.52 0.63 1 1.43 0.00 1 3 2 0.81 -0.38 0.03
Q5_1 8 490 1.73 0.77 2 1.66 1.48 1 3 2 0.50 -1.16 0.03
Q5_2 9 490 2.00 0.86 2 2.00 1.48 1 3 2 0.00 -1.64 0.04
Q5_3 10 490 1.79 0.81 2 1.73 1.48 1 3 2 0.41 -1.37 0.04
Q5_5 11 490 2.33 0.81 3 2.41 0.00 1 3 2 -0.67 -1.18 0.04
Q5_6 12 490 1.94 0.77 2 1.93 1.48 1 3 2 0.09 -1.33 0.03
Q5_12 13 490 1.92 0.78 2 1.90 1.48 1 3 2 0.14 -1.36 0.04
Q6_2 14 490 1.40 0.67 1 1.24 0.00 1 3 2 1.42 0.64 0.03
Q6_5 15 490 1.66 0.80 1 1.58 0.00 1 3 2 0.68 -1.11 0.04
Q6_6 16 490 1.22 0.52 1 1.09 0.00 1 3 2 2.29 4.28 0.02
Q6_7 17 490 1.45 0.66 1 1.32 0.00 1 3 2 1.17 0.14 0.03
Q6_8 18 490 1.43 0.65 1 1.31 0.00 1 3 2 1.21 0.27 0.03
Q6_11 19 490 1.85 0.76 2 1.81 1.48 1 3 2 0.26 -1.22 0.03
Q7_2 20 490 1.74 0.69 2 1.67 1.48 1 3 2 0.39 -0.89 0.03
Q7_4 21 490 1.89 0.79 2 1.86 1.48 1 3 2 0.20 -1.37 0.04
Q7_5 22 490 1.89 0.76 2 1.86 1.48 1 3 2 0.19 -1.24 0.03
Q7_7 23 490 2.43 0.78 3 2.54 0.00 1 3 2 -0.91 -0.76 0.04
Q7_8 24 490 1.87 0.75 2 1.84 1.48 1 3 2 0.21 -1.21 0.03
Q7_14 25 490 2.39 0.76 3 2.49 0.00 1 3 2 -0.78 -0.85 0.03DWLS
mod <- '
EL =~ 1*Q4_3 + lam44*Q4_4 + lam45*Q4_5 + lam49*Q4_9 + lam411*Q4_11 + lam415*Q4_15 + lam418*Q4_18
SC =~ 1*Q5_1 + lam52*Q5_2 + lam53*Q5_3 + lam55*Q5_5 + lam56*Q5_6 + lam512*Q5_12
IN =~ 1*Q6_2 + lam65*Q6_5 + lam66*Q6_6 + lam67*Q6_7 + lam68*Q6_8 + lam611*Q6_11
EN =~ 1*Q7_2 + lam74*Q7_4 + lam75*Q7_5 + lam77*Q7_7 + lam78*Q7_8 + lam714*Q7_14
# Factor covarainces
EL ~~ EL + SC + IN + EN
SC ~~ SC + IN + EN
IN ~~ IN + EN
EN ~~ EN
# Factor Reliabilities
rEL := ((1 + lam44 + lam45 + lam49 + lam411 + lam415 + lam418)**2)/((1 + lam44 + lam45 + lam49 + lam411 + lam415 + lam418)**2 + 7)
rSC := ((1 + lam52 + lam53 + lam55 + lam56 + lam512)**2)/((1 + lam52 + lam53 + lam55 + lam56 + lam512)**2 + 6)
rIN := ((1 + lam65 + lam66 + lam67 + lam68 + lam611)**2)/((1 + lam65 + lam66 + lam67 + lam68 + lam611)**2 + 6)
rEN := ((1 + lam74 + lam75 + lam77 + lam78 + lam714)**2)/((1 + lam74 + lam75 + lam77 + lam78 + lam714)**2 + 6)
'
fit.dwls <- lavaan::cfa(mod, data=mydata, ordered=T, parameterization="theta")
summary(fit.dwls, standardized=T, fit.measures=T)lavaan 0.6-7 ended normally after 66 iterations
Estimator DWLS
Optimization method NLMINB
Number of free parameters 81
Number of observations 490
Model Test User Model:
Standard Robust
Test Statistic 593.869 765.951
Degrees of freedom 269 269
P-value (Chi-square) 0.000 0.000
Scaling correction factor 0.883
Shift parameter 93.760
simple second-order correction
Model Test Baseline Model:
Test statistic 32729.962 10489.239
Degrees of freedom 300 300
P-value 0.000 0.000
Scaling correction factor 3.183
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.990 0.951
Tucker-Lewis Index (TLI) 0.989 0.946
Robust Comparative Fit Index (CFI) NA
Robust Tucker-Lewis Index (TLI) NA
Root Mean Square Error of Approximation:
RMSEA 0.050 0.061
90 Percent confidence interval - lower 0.044 0.056
90 Percent confidence interval - upper 0.055 0.067
P-value RMSEA <= 0.05 0.529 0.000
Robust RMSEA NA
90 Percent confidence interval - lower NA
90 Percent confidence interval - upper NA
Standardized Root Mean Square Residual:
SRMR 0.065 0.065
Parameter Estimates:
Standard errors Robust.sem
Information Expected
Information saturated (h1) model Unstructured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL =~
Q4_3 1.000 1.234 0.777
Q4_4 (lm44) 1.445 0.145 9.972 0.000 1.783 0.872
Q4_5 (lm45) 0.949 0.101 9.390 0.000 1.171 0.760
Q4_9 (lm49) 0.763 0.084 9.048 0.000 0.942 0.686
Q4_11 (l411) 1.048 0.110 9.536 0.000 1.293 0.791
Q4_15 (l415) 0.994 0.107 9.309 0.000 1.227 0.775
Q4_18 (l418) 1.272 0.137 9.295 0.000 1.569 0.843
SC =~
Q5_1 1.000 1.082 0.734
Q5_2 (lm52) 0.976 0.119 8.171 0.000 1.056 0.726
Q5_3 (lm53) 0.944 0.124 7.587 0.000 1.021 0.714
Q5_5 (lm55) 0.803 0.114 7.052 0.000 0.869 0.656
Q5_6 (lm56) 1.224 0.162 7.549 0.000 1.324 0.798
Q5_12 (l512) 1.188 0.160 7.446 0.000 1.286 0.789
IN =~
Q6_2 1.000 1.054 0.725
Q6_5 (lm65) 0.618 0.095 6.522 0.000 0.651 0.546
Q6_6 (lm66) 1.704 0.290 5.882 0.000 1.796 0.874
Q6_7 (lm67) 1.518 0.220 6.893 0.000 1.600 0.848
Q6_8 (lm68) 1.234 0.157 7.839 0.000 1.301 0.793
Q6_11 (l611) 1.602 0.256 6.258 0.000 1.688 0.860
EN =~
Q7_2 1.000 1.243 0.779
Q7_4 (lm74) 0.800 0.088 9.095 0.000 0.994 0.705
Q7_5 (lm75) 1.108 0.132 8.392 0.000 1.378 0.809
Q7_7 (lm77) 0.875 0.125 6.996 0.000 1.087 0.736
Q7_8 (lm78) 0.867 0.095 9.155 0.000 1.078 0.733
Q7_14 (l714) 0.672 0.088 7.626 0.000 0.835 0.641
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL ~~
SC 0.915 0.139 6.573 0.000 0.685 0.685
IN 0.973 0.152 6.402 0.000 0.748 0.748
EN 1.193 0.161 7.417 0.000 0.778 0.778
SC ~~
IN 0.740 0.129 5.718 0.000 0.649 0.649
EN 1.080 0.161 6.691 0.000 0.803 0.803
IN ~~
EN 0.979 0.156 6.265 0.000 0.747 0.747
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q4_3 0.000 0.000 0.000
.Q4_4 0.000 0.000 0.000
.Q4_5 0.000 0.000 0.000
.Q4_9 0.000 0.000 0.000
.Q4_11 0.000 0.000 0.000
.Q4_15 0.000 0.000 0.000
.Q4_18 0.000 0.000 0.000
.Q5_1 0.000 0.000 0.000
.Q5_2 0.000 0.000 0.000
.Q5_3 0.000 0.000 0.000
.Q5_5 0.000 0.000 0.000
.Q5_6 0.000 0.000 0.000
.Q5_12 0.000 0.000 0.000
.Q6_2 0.000 0.000 0.000
.Q6_5 0.000 0.000 0.000
.Q6_6 0.000 0.000 0.000
.Q6_7 0.000 0.000 0.000
.Q6_8 0.000 0.000 0.000
.Q6_11 0.000 0.000 0.000
.Q7_2 0.000 0.000 0.000
.Q7_4 0.000 0.000 0.000
.Q7_5 0.000 0.000 0.000
.Q7_7 0.000 0.000 0.000
.Q7_8 0.000 0.000 0.000
.Q7_14 0.000 0.000 0.000
EL 0.000 0.000 0.000
SC 0.000 0.000 0.000
IN 0.000 0.000 0.000
EN 0.000 0.000 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Q4_3|t1 -0.106 0.090 -1.181 0.238 -0.106 -0.067
Q4_3|t2 2.073 0.136 15.218 0.000 2.073 1.305
Q4_4|t1 -0.241 0.115 -2.098 0.036 -0.241 -0.118
Q4_4|t2 2.644 0.185 14.260 0.000 2.644 1.293
Q4_5|t1 0.317 0.090 3.516 0.000 0.317 0.206
Q4_5|t2 1.938 0.128 15.163 0.000 1.938 1.259
Q4_9|t1 0.091 0.078 1.168 0.243 0.091 0.067
Q4_9|t2 1.292 0.097 13.316 0.000 1.292 0.941
Q4_11|t1 0.017 0.093 0.180 0.857 0.017 0.010
Q4_11|t2 1.716 0.126 13.628 0.000 1.716 1.050
Q4_15|t1 0.105 0.091 1.163 0.245 0.105 0.067
Q4_15|t2 1.974 0.139 14.200 0.000 1.974 1.247
Q4_18|t1 0.258 0.109 2.368 0.018 0.258 0.139
Q4_18|t2 2.672 0.190 14.079 0.000 2.672 1.436
Q5_1|t1 -0.121 0.083 -1.451 0.147 -0.121 -0.082
Q5_1|t2 1.251 0.104 12.001 0.000 1.251 0.849
Q5_2|t1 -0.493 0.085 -5.781 0.000 -0.493 -0.339
Q5_2|t2 0.501 0.084 5.987 0.000 0.501 0.344
Q5_3|t1 -0.146 0.081 -1.813 0.070 -0.146 -0.102
Q5_3|t2 0.987 0.094 10.505 0.000 0.987 0.691
Q5_5|t1 -1.021 0.090 -11.329 0.000 -1.021 -0.771
Q5_5|t2 -0.163 0.076 -2.143 0.032 -0.163 -0.123
Q5_6|t1 -0.737 0.101 -7.317 0.000 -0.737 -0.444
Q5_6|t2 1.000 0.106 9.460 0.000 1.000 0.602
Q5_12|t1 -0.641 0.098 -6.572 0.000 -0.641 -0.394
Q5_12|t2 1.001 0.108 9.310 0.000 1.001 0.615
Q6_2|t1 0.788 0.098 8.044 0.000 0.788 0.542
Q6_2|t2 1.845 0.133 13.877 0.000 1.845 1.270
Q6_5|t1 0.128 0.068 1.886 0.059 0.128 0.108
Q6_5|t2 0.979 0.079 12.392 0.000 0.979 0.820
Q6_6|t1 1.934 0.262 7.394 0.000 1.934 0.941
Q6_6|t2 3.402 0.391 8.706 0.000 3.402 1.655
Q6_7|t1 0.701 0.126 5.564 0.000 0.701 0.372
Q6_7|t2 2.509 0.216 11.601 0.000 2.509 1.330
Q6_8|t1 0.655 0.107 6.131 0.000 0.655 0.399
Q6_8|t2 2.244 0.170 13.237 0.000 2.244 1.368
Q6_11|t1 -0.633 0.120 -5.279 0.000 -0.633 -0.323
Q6_11|t2 1.513 0.156 9.676 0.000 1.513 0.771
Q7_2|t1 -0.396 0.092 -4.325 0.000 -0.396 -0.248
Q7_2|t2 1.718 0.125 13.767 0.000 1.718 1.077
Q7_4|t1 -0.455 0.081 -5.608 0.000 -0.455 -0.323
Q7_4|t2 0.911 0.087 10.467 0.000 0.911 0.646
Q7_5|t1 -0.661 0.101 -6.551 0.000 -0.661 -0.388
Q7_5|t2 1.220 0.107 11.362 0.000 1.220 0.717
Q7_7|t1 -1.343 0.116 -11.624 0.000 -1.343 -0.909
Q7_7|t2 -0.421 0.090 -4.696 0.000 -0.421 -0.285
Q7_8|t1 -0.546 0.086 -6.388 0.000 -0.546 -0.372
Q7_8|t2 1.103 0.093 11.889 0.000 1.103 0.750
Q7_14|t1 -1.257 0.095 -13.256 0.000 -1.257 -0.965
Q7_14|t2 -0.187 0.075 -2.503 0.012 -0.187 -0.144
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL 1.522 0.237 6.417 0.000 1.000 1.000
SC 1.171 0.229 5.119 0.000 1.000 1.000
IN 1.111 0.234 4.753 0.000 1.000 1.000
EN 1.545 0.275 5.620 0.000 1.000 1.000
.Q4_3 1.000 1.000 0.396
.Q4_4 1.000 1.000 0.239
.Q4_5 1.000 1.000 0.422
.Q4_9 1.000 1.000 0.530
.Q4_11 1.000 1.000 0.374
.Q4_15 1.000 1.000 0.399
.Q4_18 1.000 1.000 0.289
.Q5_1 1.000 1.000 0.461
.Q5_2 1.000 1.000 0.473
.Q5_3 1.000 1.000 0.490
.Q5_5 1.000 1.000 0.570
.Q5_6 1.000 1.000 0.363
.Q5_12 1.000 1.000 0.377
.Q6_2 1.000 1.000 0.474
.Q6_5 1.000 1.000 0.702
.Q6_6 1.000 1.000 0.237
.Q6_7 1.000 1.000 0.281
.Q6_8 1.000 1.000 0.371
.Q6_11 1.000 1.000 0.260
.Q7_2 1.000 1.000 0.393
.Q7_4 1.000 1.000 0.503
.Q7_5 1.000 1.000 0.345
.Q7_7 1.000 1.000 0.458
.Q7_8 1.000 1.000 0.463
.Q7_14 1.000 1.000 0.589
Scales y*:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Q4_3 0.630 0.630 1.000
Q4_4 0.489 0.489 1.000
Q4_5 0.650 0.650 1.000
Q4_9 0.728 0.728 1.000
Q4_11 0.612 0.612 1.000
Q4_15 0.632 0.632 1.000
Q4_18 0.537 0.537 1.000
Q5_1 0.679 0.679 1.000
Q5_2 0.688 0.688 1.000
Q5_3 0.700 0.700 1.000
Q5_5 0.755 0.755 1.000
Q5_6 0.603 0.603 1.000
Q5_12 0.614 0.614 1.000
Q6_2 0.688 0.688 1.000
Q6_5 0.838 0.838 1.000
Q6_6 0.486 0.486 1.000
Q6_7 0.530 0.530 1.000
Q6_8 0.609 0.609 1.000
Q6_11 0.510 0.510 1.000
Q7_2 0.627 0.627 1.000
Q7_4 0.709 0.709 1.000
Q7_5 0.587 0.587 1.000
Q7_7 0.677 0.677 1.000
Q7_8 0.680 0.680 1.000
Q7_14 0.768 0.768 1.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
rEL 0.889 0.013 68.903 0.000 0.920 0.824
rSC 0.863 0.020 42.191 0.000 0.878 0.785
rIN 0.908 0.016 56.391 0.000 0.915 0.801
rEN 0.825 0.022 37.817 0.000 0.871 0.781Model 1: Traditional IFA
Model details
cat(read_file(paste0(w.d, "/code/pools_study/model_ifa.txt")))model {
### Model
for(p in 1:N){
for(i in 1:nit){
# data model
y[p,i] ~ dcat(pi[p,i, ])
# LRV
ystar[p,i] ~ dnorm(lambda[i]*ksi[p,map[nit]], 1)
# Pr(nu = 3)
pi[p,i,3] = phi(ystar[p,i] - tau[i,2])
# Pr(nu = 2)
pi[p,i,2] = phi(ystar[p,i] - tau[i,1]) - phi(ystar[p,i] - tau[i,2])
# Pr(nu = 1)
pi[p,i,1] = 1 - phi(ystar[p,i] - tau[i,1])
}
}
### Priors
# person parameters
for(p in 1:N){
#eta[p] ~ dnorm(0, 1) # latent ability
ksi[p, 1:M] ~ dmnorm(kappa[], inv.phi[,])
}
for(m in 1:M){
kappa[m] <- 0 # Means of latent variables
}
inv.phi[1:M,1:M] ~ dwish(dxphi.0[ , ], d); # prior for precision matrix for the latent variables
phi[1:M,1:M] <- inverse(inv.phi[ , ]); # the covariance matrix for the latent vars
for(m in 1:M){
for(mm in 1:M){
dxphi.0[m,mm] <- d*phi.0[m,mm];
}
}
# factor correlations
for(m in 1:M){
for(mm in 1:M){
phi.cor[m,mm] = (phi[m,mm])/((pow(phi[m,m], 0.5))*(pow(phi[mm,mm], 0.5)));
}
}
# priors for loadings
# loadings
lambda[1] = 1
lambda[8] = 1
lambda[13] = 1
lambda[19] = 1
for(i in 2:7){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 9:12){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 14:18){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 20:25){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 1:nit){
# Thresholds
tau[i, 1] = 0
tau[i, 2] ~ dnorm(0, 0.1)T(tau[i, 1],)
# LRV total variance
# total variance = residual variance + fact. Var.
theta[i] = 1 + pow(lambda[i],2)
# standardized loading
lambda.std[i] = lambda[i]/pow(theta[i],0.5)
}
# compute omega
lambda_sum1[1] = lambda[1]
lambda_sum2[1] = lambda[8]
lambda_sum3[1] = lambda[13]
lambda_sum4[1] = lambda[19]
for(i in 2:6){
#lambda_sum (sum factor loadings)
lambda_sum1[i] = lambda_sum1[i-1]+lambda[i]
lambda_sum2[i] = lambda_sum2[i-1]+lambda[i+7]
lambda_sum3[i] = lambda_sum3[i-1]+lambda[i+12]
lambda_sum4[i] = lambda_sum4[i-1]+lambda[i+18]
}
lambda_sum1[7] = lambda_sum1[6] + lambda[7]
# compute reliability
reli.omega[1] = (pow(lambda_sum1[7],2))/(pow(lambda_sum1[7],2)+7)
reli.omega[2] = (pow(lambda_sum2[6],2))/(pow(lambda_sum2[6],2)+6)
reli.omega[3] = (pow(lambda_sum3[6],2))/(pow(lambda_sum3[6],2)+6)
reli.omega[4] = (pow(lambda_sum4[6],2))/(pow(lambda_sum4[6],2)+6)
}Model results
# Save parameters
jags.params <- c("tau", "lambda", "theta", "reli.omega", "lambda.std",
"phi.cor", "inv.phi", "phi")
# initial-values
jags.inits <- function(){
list(
"inv.phi"=solve(matrix(
c(1.52, 0.92, 0.97, 1.19,
0.92, 1.17, 0.74, 1.08,
0.97, 0.74, 1.11, 0.98,
1.19, 1.08, 0.98, 1.55), ncol=4, nrow=4, byrow=T
))
)
}
# data
jags.data <- list(
y = mydata,
N = nrow(mydata),
nit = ncol(mydata),
map = c(rep(1,7), rep(2,6), rep(3,6), rep(4,6)),
d = 8,
M = 4,
phi.0 = matrix(
c(1, 0.69, 0.75, 0.78,
0.69, 1, 0.65, 0.80,
0.75, 0.65, 1, 0.75,
0.78, 0.80, 0.75, 1), ncol=4, nrow=4, byrow=T
)
)
model.fit <- R2jags::jags(
model = paste0(w.d, "/code/pools_study/model_ifa.txt"),
parameters.to.save = jags.params,
inits = jags.inits,
data = jags.data,
n.chains = 4,
n.burnin = 5000,
n.iter = 10000
)module glm loadedCompiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 12250
Unobserved stochastic nodes: 12787
Total graph size: 122291
Initializing modelprint(model.fit, width=1000)Inference for Bugs model at "C:/Users/noahp/Documents/GitHub/Padgett-Dissertation/code/pools_study/model_ifa.txt", fit using jags,
4 chains, each with 10000 iterations (first 5000 discarded), n.thin = 5
n.sims = 4000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
inv.phi[1,1] 3.156 1.614 0.760 2.008 2.900 4.000 7.169 1.03 140
inv.phi[2,1] -0.460 1.056 -2.762 -1.056 -0.414 0.219 1.509 1.02 160
inv.phi[3,1] -1.252 1.105 -3.846 -1.855 -1.116 -0.456 0.492 1.01 230
inv.phi[4,1] -1.271 1.433 -4.447 -2.124 -1.135 -0.283 1.152 1.01 310
inv.phi[1,2] -0.460 1.056 -2.762 -1.056 -0.414 0.219 1.509 1.02 160
inv.phi[2,2] 2.869 1.461 0.891 1.777 2.594 3.680 6.307 1.01 250
inv.phi[3,2] -0.135 0.898 -1.976 -0.681 -0.115 0.424 1.689 1.01 490
inv.phi[4,2] -1.766 1.409 -4.945 -2.551 -1.569 -0.786 0.497 1.02 180
inv.phi[1,3] -1.252 1.105 -3.846 -1.855 -1.116 -0.456 0.492 1.01 230
inv.phi[2,3] -0.135 0.898 -1.976 -0.681 -0.115 0.424 1.689 1.01 490
inv.phi[3,3] 2.748 1.319 0.722 1.799 2.512 3.474 5.946 1.02 180
inv.phi[4,3] -1.000 1.135 -3.497 -1.667 -0.889 -0.225 0.910 1.01 280
inv.phi[1,4] -1.271 1.433 -4.447 -2.124 -1.135 -0.283 1.152 1.01 310
inv.phi[2,4] -1.766 1.409 -4.945 -2.551 -1.569 -0.786 0.497 1.02 180
inv.phi[3,4] -1.000 1.135 -3.497 -1.667 -0.889 -0.225 0.910 1.01 280
inv.phi[4,4] 4.019 2.103 0.992 2.441 3.660 5.165 9.062 1.03 130
lambda[1] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[2] 1.241 0.109 1.034 1.165 1.239 1.315 1.461 1.00 1600
lambda[3] 0.789 0.080 0.640 0.734 0.786 0.839 0.956 1.00 1500
lambda[4] 0.780 0.081 0.632 0.724 0.777 0.835 0.945 1.00 1100
lambda[5] 0.997 0.092 0.831 0.934 0.994 1.056 1.185 1.00 660
lambda[6] 0.916 0.085 0.756 0.858 0.914 0.972 1.094 1.00 1500
lambda[7] 1.000 0.095 0.824 0.933 0.997 1.061 1.195 1.01 380
lambda[8] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[9] 0.865 0.083 0.709 0.808 0.863 0.920 1.030 1.00 900
lambda[10] 0.769 0.075 0.629 0.717 0.767 0.818 0.923 1.00 1500
lambda[11] 0.732 0.078 0.587 0.679 0.730 0.783 0.893 1.00 3000
lambda[12] 1.025 0.089 0.857 0.965 1.024 1.082 1.205 1.00 3900
lambda[13] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[14] 0.421 0.064 0.298 0.378 0.419 0.462 0.550 1.00 1300
lambda[15] 0.471 0.062 0.351 0.429 0.471 0.511 0.596 1.00 1300
lambda[16] 0.292 0.062 0.175 0.250 0.292 0.332 0.416 1.00 2100
lambda[17] 0.658 0.074 0.519 0.609 0.656 0.706 0.810 1.00 560
lambda[18] 0.542 0.069 0.414 0.495 0.539 0.587 0.685 1.00 840
lambda[19] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[20] 1.142 0.099 0.956 1.072 1.141 1.207 1.343 1.00 1400
lambda[21] 0.966 0.085 0.805 0.906 0.965 1.022 1.141 1.00 2400
lambda[22] 1.197 0.104 1.006 1.126 1.194 1.264 1.410 1.00 1200
lambda[23] 0.883 0.087 0.719 0.825 0.880 0.940 1.062 1.00 1700
lambda[24] 1.002 0.087 0.840 0.943 0.999 1.060 1.176 1.00 1600
lambda[25] 0.770 0.079 0.623 0.713 0.769 0.822 0.929 1.00 640
lambda.std[1] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[2] 0.777 0.027 0.719 0.759 0.778 0.796 0.825 1.00 1900
lambda.std[3] 0.617 0.039 0.539 0.592 0.618 0.643 0.691 1.00 1500
lambda.std[4] 0.613 0.040 0.534 0.586 0.614 0.641 0.687 1.00 1100
lambda.std[5] 0.704 0.032 0.639 0.683 0.705 0.726 0.764 1.00 690
lambda.std[6] 0.673 0.034 0.603 0.651 0.675 0.697 0.738 1.00 1400
lambda.std[7] 0.705 0.033 0.636 0.682 0.706 0.728 0.767 1.01 370
lambda.std[8] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[9] 0.652 0.036 0.579 0.628 0.653 0.677 0.718 1.00 830
lambda.std[10] 0.608 0.037 0.532 0.583 0.609 0.633 0.678 1.00 1500
lambda.std[11] 0.588 0.041 0.506 0.562 0.590 0.617 0.666 1.00 3100
lambda.std[12] 0.714 0.030 0.651 0.695 0.715 0.734 0.769 1.00 3600
lambda.std[13] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[14] 0.386 0.050 0.286 0.354 0.386 0.419 0.482 1.00 1400
lambda.std[15] 0.424 0.046 0.331 0.394 0.426 0.455 0.512 1.00 1300
lambda.std[16] 0.279 0.054 0.172 0.243 0.280 0.315 0.384 1.00 2100
lambda.std[17] 0.548 0.043 0.460 0.520 0.549 0.577 0.629 1.00 550
lambda.std[18] 0.474 0.047 0.382 0.443 0.475 0.506 0.565 1.00 860
lambda.std[19] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[20] 0.750 0.029 0.691 0.731 0.752 0.770 0.802 1.00 1300
lambda.std[21] 0.693 0.032 0.627 0.671 0.694 0.715 0.752 1.00 2800
lambda.std[22] 0.765 0.027 0.709 0.748 0.767 0.784 0.816 1.00 1100
lambda.std[23] 0.660 0.037 0.584 0.637 0.660 0.685 0.728 1.00 1800
lambda.std[24] 0.706 0.031 0.643 0.686 0.707 0.728 0.762 1.00 1700
lambda.std[25] 0.608 0.039 0.529 0.580 0.609 0.635 0.681 1.00 660
phi[1,1] 2.621 1.631 0.856 1.636 2.254 3.045 7.216 1.03 170
phi[2,1] 1.583 0.883 0.188 1.006 1.510 2.039 3.640 1.03 1800
phi[3,1] 1.931 1.046 0.465 1.233 1.774 2.384 4.552 1.02 490
phi[4,1] 1.908 0.735 0.526 1.456 1.897 2.322 3.473 1.03 360
phi[1,2] 1.583 0.883 0.188 1.006 1.510 2.039 3.640 1.03 1800
phi[2,2] 2.078 1.022 0.723 1.368 1.900 2.517 4.717 1.02 280
phi[3,2] 1.399 0.818 0.025 0.837 1.314 1.881 3.145 1.02 200
phi[4,2] 1.677 0.701 0.186 1.261 1.715 2.117 3.064 1.02 270
phi[1,3] 1.931 1.046 0.465 1.233 1.774 2.384 4.552 1.02 490
phi[2,3] 1.399 0.818 0.025 0.837 1.314 1.881 3.145 1.02 200
phi[3,3] 2.373 1.199 0.821 1.525 2.127 2.949 5.177 1.00 4000
phi[4,3] 1.781 0.671 0.426 1.336 1.785 2.224 3.074 1.00 550
phi[1,4] 1.908 0.735 0.526 1.456 1.897 2.322 3.473 1.03 360
phi[2,4] 1.677 0.701 0.186 1.261 1.715 2.117 3.064 1.02 270
phi[3,4] 1.781 0.671 0.426 1.336 1.785 2.224 3.074 1.00 550
phi[4,4] 2.290 0.242 1.855 2.124 2.279 2.439 2.811 1.00 1800
phi.cor[1,1] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[2,1] 0.696 0.210 0.125 0.620 0.752 0.842 0.925 1.03 200
phi.cor[3,1] 0.784 0.157 0.368 0.723 0.833 0.895 0.951 1.01 780
phi.cor[4,1] 0.799 0.172 0.319 0.750 0.860 0.908 0.952 1.03 890
phi.cor[1,2] 0.696 0.210 0.125 0.620 0.752 0.842 0.925 1.03 200
phi.cor[2,2] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[3,2] 0.642 0.241 0.022 0.533 0.707 0.821 0.914 1.02 170
phi.cor[4,2] 0.769 0.215 0.109 0.724 0.849 0.903 0.952 1.05 210
phi.cor[1,3] 0.784 0.157 0.368 0.723 0.833 0.895 0.951 1.01 780
phi.cor[2,3] 0.642 0.241 0.022 0.533 0.707 0.821 0.914 1.02 170
phi.cor[3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[4,3] 0.772 0.178 0.237 0.721 0.828 0.887 0.941 1.02 200
phi.cor[1,4] 0.799 0.172 0.319 0.750 0.860 0.908 0.952 1.03 890
phi.cor[2,4] 0.769 0.215 0.109 0.724 0.849 0.903 0.952 1.05 210
phi.cor[3,4] 0.772 0.178 0.237 0.721 0.828 0.887 0.941 1.02 200
phi.cor[4,4] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
reli.omega[1] 0.865 0.011 0.843 0.858 0.866 0.873 0.886 1.01 430
reli.omega[2] 0.828 0.011 0.807 0.821 0.829 0.836 0.849 1.00 4000
reli.omega[3] 0.655 0.025 0.604 0.638 0.655 0.672 0.703 1.01 410
reli.omega[4] 0.864 0.011 0.842 0.857 0.864 0.872 0.884 1.00 3100
tau[1,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[4,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[5,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[6,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[7,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[8,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[9,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[10,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[11,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[12,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[13,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[14,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[15,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[16,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[17,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[18,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[19,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[20,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[21,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[22,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[23,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[24,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[25,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[1,2] 2.842 0.149 2.553 2.743 2.837 2.942 3.138 1.00 3900
tau[2,2] 3.235 0.198 2.868 3.095 3.228 3.368 3.648 1.00 2300
tau[3,2] 2.353 0.152 2.062 2.247 2.349 2.454 2.648 1.00 1800
tau[4,2] 1.780 0.117 1.556 1.699 1.778 1.858 2.011 1.00 770
tau[5,2] 2.298 0.144 2.023 2.195 2.298 2.397 2.584 1.00 840
tau[6,2] 2.586 0.157 2.297 2.475 2.582 2.689 2.909 1.00 2700
tau[7,2] 3.085 0.198 2.709 2.952 3.082 3.217 3.483 1.00 1500
tau[8,2] 1.898 0.106 1.691 1.825 1.898 1.967 2.107 1.00 4000
tau[9,2] 1.095 0.081 0.941 1.040 1.094 1.150 1.258 1.00 1200
tau[10,2] 1.436 0.099 1.245 1.372 1.435 1.501 1.644 1.00 4000
tau[11,2] 0.667 0.054 0.564 0.631 0.665 0.701 0.776 1.00 3100
tau[12,2] 1.697 0.102 1.501 1.626 1.696 1.763 1.902 1.00 3300
tau[13,2] 1.678 0.090 1.505 1.615 1.677 1.740 1.856 1.00 1500
tau[14,2] 1.637 0.132 1.380 1.547 1.638 1.724 1.901 1.00 1000
tau[15,2] 1.273 0.092 1.100 1.212 1.270 1.336 1.455 1.00 2500
tau[16,2] 1.838 0.184 1.492 1.712 1.832 1.961 2.212 1.00 4000
tau[17,2] 2.208 0.155 1.910 2.103 2.205 2.310 2.525 1.00 720
tau[18,2] 2.091 0.147 1.801 1.993 2.090 2.188 2.388 1.00 1400
tau[19,2] 1.954 0.100 1.766 1.884 1.953 2.021 2.153 1.00 2000
tau[20,2] 2.643 0.153 2.352 2.537 2.640 2.745 2.953 1.00 1300
tau[21,2] 1.650 0.103 1.450 1.581 1.648 1.719 1.854 1.00 700
tau[22,2] 2.035 0.125 1.798 1.951 2.030 2.116 2.283 1.00 700
tau[23,2] 0.583 0.051 0.488 0.547 0.582 0.617 0.687 1.00 4000
tau[24,2] 1.907 0.110 1.702 1.832 1.904 1.983 2.132 1.00 1000
tau[25,2] 0.745 0.056 0.641 0.706 0.744 0.783 0.862 1.00 2300
theta[1] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[2] 2.553 0.272 2.069 2.357 2.536 2.729 3.135 1.00 1400
theta[3] 1.628 0.128 1.409 1.539 1.617 1.704 1.914 1.00 1500
theta[4] 1.615 0.128 1.399 1.524 1.604 1.697 1.893 1.00 1300
theta[5] 2.003 0.185 1.691 1.873 1.989 2.116 2.405 1.00 630
theta[6] 1.847 0.157 1.572 1.736 1.836 1.946 2.198 1.00 1600
theta[7] 2.009 0.192 1.679 1.871 1.995 2.127 2.429 1.01 390
theta[8] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[9] 1.755 0.145 1.503 1.653 1.744 1.846 2.061 1.00 1000
theta[10] 1.597 0.117 1.395 1.514 1.589 1.670 1.852 1.00 1500
theta[11] 1.542 0.115 1.344 1.461 1.533 1.613 1.797 1.00 2900
theta[12] 2.059 0.184 1.734 1.932 2.048 2.170 2.451 1.00 4000
theta[13] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[14] 1.181 0.055 1.089 1.143 1.175 1.213 1.302 1.00 1300
theta[15] 1.225 0.059 1.123 1.184 1.222 1.261 1.355 1.00 1500
theta[16] 1.089 0.037 1.031 1.063 1.085 1.111 1.173 1.00 3100
theta[17] 1.439 0.099 1.269 1.371 1.430 1.499 1.655 1.00 580
theta[18] 1.298 0.076 1.171 1.245 1.291 1.344 1.470 1.00 810
theta[19] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[20] 2.313 0.228 1.913 2.150 2.302 2.457 2.805 1.00 1500
theta[21] 1.941 0.166 1.648 1.821 1.931 2.044 2.301 1.00 2100
theta[22] 2.445 0.253 2.013 2.267 2.425 2.597 2.987 1.00 1300
theta[23] 1.788 0.155 1.517 1.681 1.774 1.884 2.127 1.00 1500
theta[24] 2.012 0.175 1.705 1.889 1.999 2.125 2.383 1.00 1500
theta[25] 1.599 0.123 1.388 1.508 1.591 1.676 1.863 1.00 610
deviance 15091.744 119.045 14858.102 15012.531 15091.659 15170.140 15327.725 1.00 4000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 7086.0 and DIC = 22177.7
DIC is an estimate of expected predictive error (lower deviance is better).kable(model.fit$BUGSoutput$summary, format="html", digits=3) %>%
kable_styling(full_width = T) %>%
scroll_box(width="100%", height="500px")| mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | Rhat | n.eff | |
|---|---|---|---|---|---|---|---|---|---|
| deviance | 15091.744 | 119.045 | 14858.102 | 15012.531 | 15091.659 | 15170.140 | 15327.725 | 1.00 | 4000 |
| inv.phi[1,1] | 3.156 | 1.614 | 0.760 | 2.008 | 2.900 | 4.000 | 7.169 | 1.03 | 140 |
| inv.phi[2,1] | -0.460 | 1.056 | -2.762 | -1.056 | -0.414 | 0.219 | 1.509 | 1.02 | 160 |
| inv.phi[3,1] | -1.252 | 1.105 | -3.846 | -1.855 | -1.116 | -0.456 | 0.492 | 1.01 | 230 |
| inv.phi[4,1] | -1.271 | 1.433 | -4.447 | -2.124 | -1.135 | -0.283 | 1.152 | 1.01 | 310 |
| inv.phi[1,2] | -0.460 | 1.056 | -2.762 | -1.056 | -0.414 | 0.219 | 1.509 | 1.02 | 160 |
| inv.phi[2,2] | 2.869 | 1.461 | 0.891 | 1.777 | 2.594 | 3.680 | 6.307 | 1.01 | 250 |
| inv.phi[3,2] | -0.135 | 0.898 | -1.976 | -0.681 | -0.115 | 0.424 | 1.689 | 1.01 | 490 |
| inv.phi[4,2] | -1.766 | 1.409 | -4.945 | -2.551 | -1.569 | -0.786 | 0.497 | 1.02 | 180 |
| inv.phi[1,3] | -1.252 | 1.105 | -3.846 | -1.855 | -1.116 | -0.456 | 0.492 | 1.01 | 230 |
| inv.phi[2,3] | -0.135 | 0.898 | -1.976 | -0.681 | -0.115 | 0.424 | 1.689 | 1.01 | 490 |
| inv.phi[3,3] | 2.748 | 1.319 | 0.722 | 1.799 | 2.512 | 3.474 | 5.946 | 1.02 | 180 |
| inv.phi[4,3] | -1.000 | 1.135 | -3.497 | -1.667 | -0.889 | -0.225 | 0.910 | 1.01 | 280 |
| inv.phi[1,4] | -1.271 | 1.433 | -4.447 | -2.124 | -1.135 | -0.283 | 1.152 | 1.01 | 310 |
| inv.phi[2,4] | -1.766 | 1.409 | -4.945 | -2.551 | -1.569 | -0.786 | 0.497 | 1.02 | 180 |
| inv.phi[3,4] | -1.000 | 1.135 | -3.497 | -1.667 | -0.889 | -0.225 | 0.910 | 1.01 | 280 |
| inv.phi[4,4] | 4.019 | 2.103 | 0.992 | 2.441 | 3.660 | 5.165 | 9.062 | 1.03 | 130 |
| lambda[1] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[2] | 1.241 | 0.109 | 1.034 | 1.165 | 1.239 | 1.315 | 1.461 | 1.00 | 1600 |
| lambda[3] | 0.789 | 0.080 | 0.640 | 0.734 | 0.786 | 0.839 | 0.956 | 1.00 | 1500 |
| lambda[4] | 0.780 | 0.081 | 0.632 | 0.724 | 0.777 | 0.835 | 0.945 | 1.00 | 1100 |
| lambda[5] | 0.997 | 0.092 | 0.831 | 0.934 | 0.994 | 1.056 | 1.185 | 1.00 | 660 |
| lambda[6] | 0.916 | 0.085 | 0.756 | 0.858 | 0.914 | 0.972 | 1.094 | 1.00 | 1500 |
| lambda[7] | 1.000 | 0.095 | 0.824 | 0.933 | 0.997 | 1.061 | 1.195 | 1.01 | 380 |
| lambda[8] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[9] | 0.865 | 0.083 | 0.709 | 0.808 | 0.863 | 0.920 | 1.030 | 1.00 | 900 |
| lambda[10] | 0.769 | 0.075 | 0.629 | 0.717 | 0.767 | 0.818 | 0.923 | 1.00 | 1500 |
| lambda[11] | 0.732 | 0.078 | 0.587 | 0.679 | 0.730 | 0.783 | 0.893 | 1.00 | 3000 |
| lambda[12] | 1.025 | 0.089 | 0.857 | 0.965 | 1.024 | 1.082 | 1.205 | 1.00 | 3900 |
| lambda[13] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[14] | 0.421 | 0.064 | 0.298 | 0.378 | 0.419 | 0.462 | 0.550 | 1.00 | 1300 |
| lambda[15] | 0.471 | 0.062 | 0.351 | 0.429 | 0.471 | 0.511 | 0.596 | 1.00 | 1300 |
| lambda[16] | 0.292 | 0.062 | 0.175 | 0.250 | 0.292 | 0.332 | 0.416 | 1.00 | 2100 |
| lambda[17] | 0.658 | 0.074 | 0.519 | 0.609 | 0.656 | 0.706 | 0.810 | 1.00 | 560 |
| lambda[18] | 0.542 | 0.069 | 0.414 | 0.495 | 0.539 | 0.587 | 0.685 | 1.00 | 840 |
| lambda[19] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[20] | 1.142 | 0.099 | 0.956 | 1.072 | 1.141 | 1.207 | 1.343 | 1.00 | 1400 |
| lambda[21] | 0.966 | 0.085 | 0.805 | 0.906 | 0.965 | 1.022 | 1.141 | 1.00 | 2400 |
| lambda[22] | 1.197 | 0.104 | 1.006 | 1.126 | 1.194 | 1.264 | 1.410 | 1.00 | 1200 |
| lambda[23] | 0.883 | 0.087 | 0.719 | 0.825 | 0.880 | 0.940 | 1.062 | 1.00 | 1700 |
| lambda[24] | 1.002 | 0.087 | 0.840 | 0.943 | 0.999 | 1.060 | 1.176 | 1.00 | 1600 |
| lambda[25] | 0.770 | 0.079 | 0.623 | 0.713 | 0.769 | 0.822 | 0.929 | 1.00 | 640 |
| lambda.std[1] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[2] | 0.777 | 0.027 | 0.719 | 0.759 | 0.778 | 0.796 | 0.825 | 1.00 | 1900 |
| lambda.std[3] | 0.617 | 0.039 | 0.539 | 0.592 | 0.618 | 0.643 | 0.691 | 1.00 | 1500 |
| lambda.std[4] | 0.613 | 0.040 | 0.534 | 0.586 | 0.614 | 0.641 | 0.687 | 1.00 | 1100 |
| lambda.std[5] | 0.704 | 0.032 | 0.639 | 0.683 | 0.705 | 0.726 | 0.764 | 1.00 | 690 |
| lambda.std[6] | 0.673 | 0.034 | 0.603 | 0.651 | 0.675 | 0.697 | 0.738 | 1.00 | 1400 |
| lambda.std[7] | 0.705 | 0.033 | 0.636 | 0.682 | 0.706 | 0.728 | 0.767 | 1.01 | 370 |
| lambda.std[8] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[9] | 0.652 | 0.036 | 0.579 | 0.628 | 0.653 | 0.677 | 0.718 | 1.00 | 830 |
| lambda.std[10] | 0.608 | 0.037 | 0.532 | 0.583 | 0.609 | 0.633 | 0.678 | 1.00 | 1500 |
| lambda.std[11] | 0.588 | 0.041 | 0.506 | 0.562 | 0.590 | 0.617 | 0.666 | 1.00 | 3100 |
| lambda.std[12] | 0.714 | 0.030 | 0.651 | 0.695 | 0.715 | 0.734 | 0.769 | 1.00 | 3600 |
| lambda.std[13] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[14] | 0.386 | 0.050 | 0.286 | 0.354 | 0.386 | 0.419 | 0.482 | 1.00 | 1400 |
| lambda.std[15] | 0.424 | 0.046 | 0.331 | 0.394 | 0.426 | 0.455 | 0.512 | 1.00 | 1300 |
| lambda.std[16] | 0.279 | 0.054 | 0.172 | 0.243 | 0.280 | 0.315 | 0.384 | 1.00 | 2100 |
| lambda.std[17] | 0.548 | 0.043 | 0.460 | 0.520 | 0.549 | 0.577 | 0.629 | 1.00 | 550 |
| lambda.std[18] | 0.474 | 0.047 | 0.382 | 0.443 | 0.475 | 0.506 | 0.565 | 1.00 | 860 |
| lambda.std[19] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[20] | 0.750 | 0.029 | 0.691 | 0.731 | 0.752 | 0.770 | 0.802 | 1.00 | 1300 |
| lambda.std[21] | 0.693 | 0.032 | 0.627 | 0.671 | 0.694 | 0.715 | 0.752 | 1.00 | 2800 |
| lambda.std[22] | 0.765 | 0.027 | 0.709 | 0.748 | 0.767 | 0.784 | 0.816 | 1.00 | 1100 |
| lambda.std[23] | 0.660 | 0.037 | 0.584 | 0.637 | 0.660 | 0.685 | 0.728 | 1.00 | 1800 |
| lambda.std[24] | 0.706 | 0.031 | 0.643 | 0.686 | 0.707 | 0.728 | 0.762 | 1.00 | 1700 |
| lambda.std[25] | 0.608 | 0.039 | 0.529 | 0.580 | 0.609 | 0.635 | 0.681 | 1.00 | 660 |
| phi[1,1] | 2.621 | 1.631 | 0.856 | 1.636 | 2.254 | 3.045 | 7.216 | 1.03 | 170 |
| phi[2,1] | 1.583 | 0.883 | 0.188 | 1.006 | 1.510 | 2.039 | 3.640 | 1.03 | 1800 |
| phi[3,1] | 1.931 | 1.046 | 0.465 | 1.233 | 1.774 | 2.384 | 4.552 | 1.02 | 490 |
| phi[4,1] | 1.908 | 0.735 | 0.526 | 1.456 | 1.897 | 2.322 | 3.473 | 1.03 | 360 |
| phi[1,2] | 1.583 | 0.883 | 0.188 | 1.006 | 1.510 | 2.039 | 3.640 | 1.03 | 1800 |
| phi[2,2] | 2.078 | 1.022 | 0.723 | 1.368 | 1.900 | 2.517 | 4.717 | 1.02 | 280 |
| phi[3,2] | 1.399 | 0.818 | 0.025 | 0.837 | 1.314 | 1.881 | 3.145 | 1.02 | 200 |
| phi[4,2] | 1.677 | 0.701 | 0.186 | 1.261 | 1.715 | 2.117 | 3.064 | 1.02 | 270 |
| phi[1,3] | 1.931 | 1.046 | 0.465 | 1.233 | 1.774 | 2.384 | 4.552 | 1.02 | 490 |
| phi[2,3] | 1.399 | 0.818 | 0.025 | 0.837 | 1.314 | 1.881 | 3.145 | 1.02 | 200 |
| phi[3,3] | 2.373 | 1.199 | 0.821 | 1.525 | 2.127 | 2.949 | 5.177 | 1.00 | 4000 |
| phi[4,3] | 1.781 | 0.671 | 0.426 | 1.336 | 1.785 | 2.224 | 3.074 | 1.00 | 550 |
| phi[1,4] | 1.908 | 0.735 | 0.526 | 1.456 | 1.897 | 2.322 | 3.473 | 1.03 | 360 |
| phi[2,4] | 1.677 | 0.701 | 0.186 | 1.261 | 1.715 | 2.117 | 3.064 | 1.02 | 270 |
| phi[3,4] | 1.781 | 0.671 | 0.426 | 1.336 | 1.785 | 2.224 | 3.074 | 1.00 | 550 |
| phi[4,4] | 2.290 | 0.242 | 1.855 | 2.124 | 2.279 | 2.439 | 2.811 | 1.00 | 1800 |
| phi.cor[1,1] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[2,1] | 0.696 | 0.210 | 0.125 | 0.620 | 0.752 | 0.842 | 0.925 | 1.03 | 200 |
| phi.cor[3,1] | 0.784 | 0.157 | 0.368 | 0.723 | 0.833 | 0.895 | 0.951 | 1.01 | 780 |
| phi.cor[4,1] | 0.799 | 0.172 | 0.319 | 0.750 | 0.860 | 0.908 | 0.952 | 1.03 | 890 |
| phi.cor[1,2] | 0.696 | 0.210 | 0.125 | 0.620 | 0.752 | 0.842 | 0.925 | 1.03 | 200 |
| phi.cor[2,2] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[3,2] | 0.642 | 0.241 | 0.022 | 0.533 | 0.707 | 0.821 | 0.914 | 1.02 | 170 |
| phi.cor[4,2] | 0.769 | 0.215 | 0.109 | 0.724 | 0.849 | 0.903 | 0.952 | 1.05 | 210 |
| phi.cor[1,3] | 0.784 | 0.157 | 0.368 | 0.723 | 0.833 | 0.895 | 0.951 | 1.01 | 780 |
| phi.cor[2,3] | 0.642 | 0.241 | 0.022 | 0.533 | 0.707 | 0.821 | 0.914 | 1.02 | 170 |
| phi.cor[3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[4,3] | 0.772 | 0.178 | 0.237 | 0.721 | 0.828 | 0.887 | 0.941 | 1.02 | 200 |
| phi.cor[1,4] | 0.799 | 0.172 | 0.319 | 0.750 | 0.860 | 0.908 | 0.952 | 1.03 | 890 |
| phi.cor[2,4] | 0.769 | 0.215 | 0.109 | 0.724 | 0.849 | 0.903 | 0.952 | 1.05 | 210 |
| phi.cor[3,4] | 0.772 | 0.178 | 0.237 | 0.721 | 0.828 | 0.887 | 0.941 | 1.02 | 200 |
| phi.cor[4,4] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| reli.omega[1] | 0.865 | 0.011 | 0.843 | 0.858 | 0.866 | 0.873 | 0.886 | 1.01 | 430 |
| reli.omega[2] | 0.828 | 0.011 | 0.807 | 0.821 | 0.829 | 0.836 | 0.849 | 1.00 | 4000 |
| reli.omega[3] | 0.655 | 0.025 | 0.604 | 0.638 | 0.655 | 0.672 | 0.703 | 1.01 | 410 |
| reli.omega[4] | 0.864 | 0.011 | 0.842 | 0.857 | 0.864 | 0.872 | 0.884 | 1.00 | 3100 |
| tau[1,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[4,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[5,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[6,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[7,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[8,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[9,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[10,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[11,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[12,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[13,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[14,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[15,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[16,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[17,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[18,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[19,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[20,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[21,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[22,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[23,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[24,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[25,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[1,2] | 2.842 | 0.149 | 2.553 | 2.743 | 2.837 | 2.942 | 3.138 | 1.00 | 3900 |
| tau[2,2] | 3.235 | 0.198 | 2.868 | 3.095 | 3.228 | 3.368 | 3.648 | 1.00 | 2300 |
| tau[3,2] | 2.353 | 0.152 | 2.062 | 2.247 | 2.349 | 2.454 | 2.648 | 1.00 | 1800 |
| tau[4,2] | 1.780 | 0.117 | 1.556 | 1.699 | 1.778 | 1.858 | 2.011 | 1.00 | 770 |
| tau[5,2] | 2.298 | 0.144 | 2.023 | 2.195 | 2.298 | 2.397 | 2.584 | 1.00 | 840 |
| tau[6,2] | 2.586 | 0.157 | 2.297 | 2.475 | 2.582 | 2.689 | 2.909 | 1.00 | 2700 |
| tau[7,2] | 3.085 | 0.198 | 2.709 | 2.952 | 3.082 | 3.217 | 3.483 | 1.00 | 1500 |
| tau[8,2] | 1.898 | 0.106 | 1.691 | 1.825 | 1.898 | 1.967 | 2.107 | 1.00 | 4000 |
| tau[9,2] | 1.095 | 0.081 | 0.941 | 1.040 | 1.094 | 1.150 | 1.258 | 1.00 | 1200 |
| tau[10,2] | 1.436 | 0.099 | 1.245 | 1.372 | 1.435 | 1.501 | 1.644 | 1.00 | 4000 |
| tau[11,2] | 0.667 | 0.054 | 0.564 | 0.631 | 0.665 | 0.701 | 0.776 | 1.00 | 3100 |
| tau[12,2] | 1.697 | 0.102 | 1.501 | 1.626 | 1.696 | 1.763 | 1.902 | 1.00 | 3300 |
| tau[13,2] | 1.678 | 0.090 | 1.505 | 1.615 | 1.677 | 1.740 | 1.856 | 1.00 | 1500 |
| tau[14,2] | 1.637 | 0.132 | 1.380 | 1.547 | 1.638 | 1.724 | 1.901 | 1.00 | 1000 |
| tau[15,2] | 1.273 | 0.092 | 1.100 | 1.212 | 1.270 | 1.336 | 1.455 | 1.00 | 2500 |
| tau[16,2] | 1.838 | 0.184 | 1.492 | 1.712 | 1.832 | 1.961 | 2.212 | 1.00 | 4000 |
| tau[17,2] | 2.208 | 0.155 | 1.910 | 2.103 | 2.205 | 2.310 | 2.525 | 1.00 | 720 |
| tau[18,2] | 2.091 | 0.147 | 1.801 | 1.993 | 2.090 | 2.188 | 2.388 | 1.00 | 1400 |
| tau[19,2] | 1.954 | 0.100 | 1.766 | 1.884 | 1.953 | 2.021 | 2.153 | 1.00 | 2000 |
| tau[20,2] | 2.643 | 0.153 | 2.352 | 2.537 | 2.640 | 2.745 | 2.953 | 1.00 | 1300 |
| tau[21,2] | 1.650 | 0.103 | 1.450 | 1.581 | 1.648 | 1.719 | 1.854 | 1.00 | 700 |
| tau[22,2] | 2.035 | 0.125 | 1.798 | 1.951 | 2.030 | 2.116 | 2.283 | 1.00 | 700 |
| tau[23,2] | 0.583 | 0.051 | 0.488 | 0.547 | 0.582 | 0.617 | 0.687 | 1.00 | 4000 |
| tau[24,2] | 1.907 | 0.110 | 1.702 | 1.832 | 1.904 | 1.983 | 2.132 | 1.00 | 1000 |
| tau[25,2] | 0.745 | 0.056 | 0.641 | 0.706 | 0.744 | 0.783 | 0.862 | 1.00 | 2300 |
| theta[1] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[2] | 2.553 | 0.272 | 2.069 | 2.357 | 2.536 | 2.729 | 3.135 | 1.00 | 1400 |
| theta[3] | 1.628 | 0.128 | 1.409 | 1.539 | 1.617 | 1.704 | 1.914 | 1.00 | 1500 |
| theta[4] | 1.615 | 0.128 | 1.399 | 1.524 | 1.604 | 1.697 | 1.893 | 1.00 | 1300 |
| theta[5] | 2.003 | 0.185 | 1.691 | 1.873 | 1.989 | 2.116 | 2.405 | 1.00 | 630 |
| theta[6] | 1.847 | 0.157 | 1.572 | 1.736 | 1.836 | 1.946 | 2.198 | 1.00 | 1600 |
| theta[7] | 2.009 | 0.192 | 1.679 | 1.871 | 1.995 | 2.127 | 2.429 | 1.01 | 390 |
| theta[8] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[9] | 1.755 | 0.145 | 1.503 | 1.653 | 1.744 | 1.846 | 2.061 | 1.00 | 1000 |
| theta[10] | 1.597 | 0.117 | 1.395 | 1.514 | 1.589 | 1.670 | 1.852 | 1.00 | 1500 |
| theta[11] | 1.542 | 0.115 | 1.344 | 1.461 | 1.533 | 1.613 | 1.797 | 1.00 | 2900 |
| theta[12] | 2.059 | 0.184 | 1.734 | 1.932 | 2.048 | 2.170 | 2.451 | 1.00 | 4000 |
| theta[13] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[14] | 1.181 | 0.055 | 1.089 | 1.143 | 1.175 | 1.213 | 1.302 | 1.00 | 1300 |
| theta[15] | 1.225 | 0.059 | 1.123 | 1.184 | 1.222 | 1.261 | 1.355 | 1.00 | 1500 |
| theta[16] | 1.089 | 0.037 | 1.031 | 1.063 | 1.085 | 1.111 | 1.173 | 1.00 | 3100 |
| theta[17] | 1.439 | 0.099 | 1.269 | 1.371 | 1.430 | 1.499 | 1.655 | 1.00 | 580 |
| theta[18] | 1.298 | 0.076 | 1.171 | 1.245 | 1.291 | 1.344 | 1.470 | 1.00 | 810 |
| theta[19] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[20] | 2.313 | 0.228 | 1.913 | 2.150 | 2.302 | 2.457 | 2.805 | 1.00 | 1500 |
| theta[21] | 1.941 | 0.166 | 1.648 | 1.821 | 1.931 | 2.044 | 2.301 | 1.00 | 2100 |
| theta[22] | 2.445 | 0.253 | 2.013 | 2.267 | 2.425 | 2.597 | 2.987 | 1.00 | 1300 |
| theta[23] | 1.788 | 0.155 | 1.517 | 1.681 | 1.774 | 1.884 | 2.127 | 1.00 | 1500 |
| theta[24] | 2.012 | 0.175 | 1.705 | 1.889 | 1.999 | 2.125 | 2.383 | 1.00 | 1500 |
| theta[25] | 1.599 | 0.123 | 1.388 | 1.508 | 1.591 | 1.676 | 1.863 | 1.00 | 610 |
Posterior Distribution Summary
# extract for plotting
jags.mcmc <- as.mcmc(model.fit)
a <- colnames(as.data.frame(jags.mcmc[[1]]))
fit.mcmc <- data.frame(as.matrix(jags.mcmc, chains = T, iters = T))
colnames(fit.mcmc) <- c("chain", "iter", a)
fit.mcmc.ggs <- ggmcmc::ggs(jags.mcmc) # for GRB plotFactor Loadings (\(\lambda\))
bayesplot::mcmc_areas(fit.mcmc, regex_pars = "lambda.std", prob = 0.8); ggsave("fig/pools_model1_lambda_dens.pdf")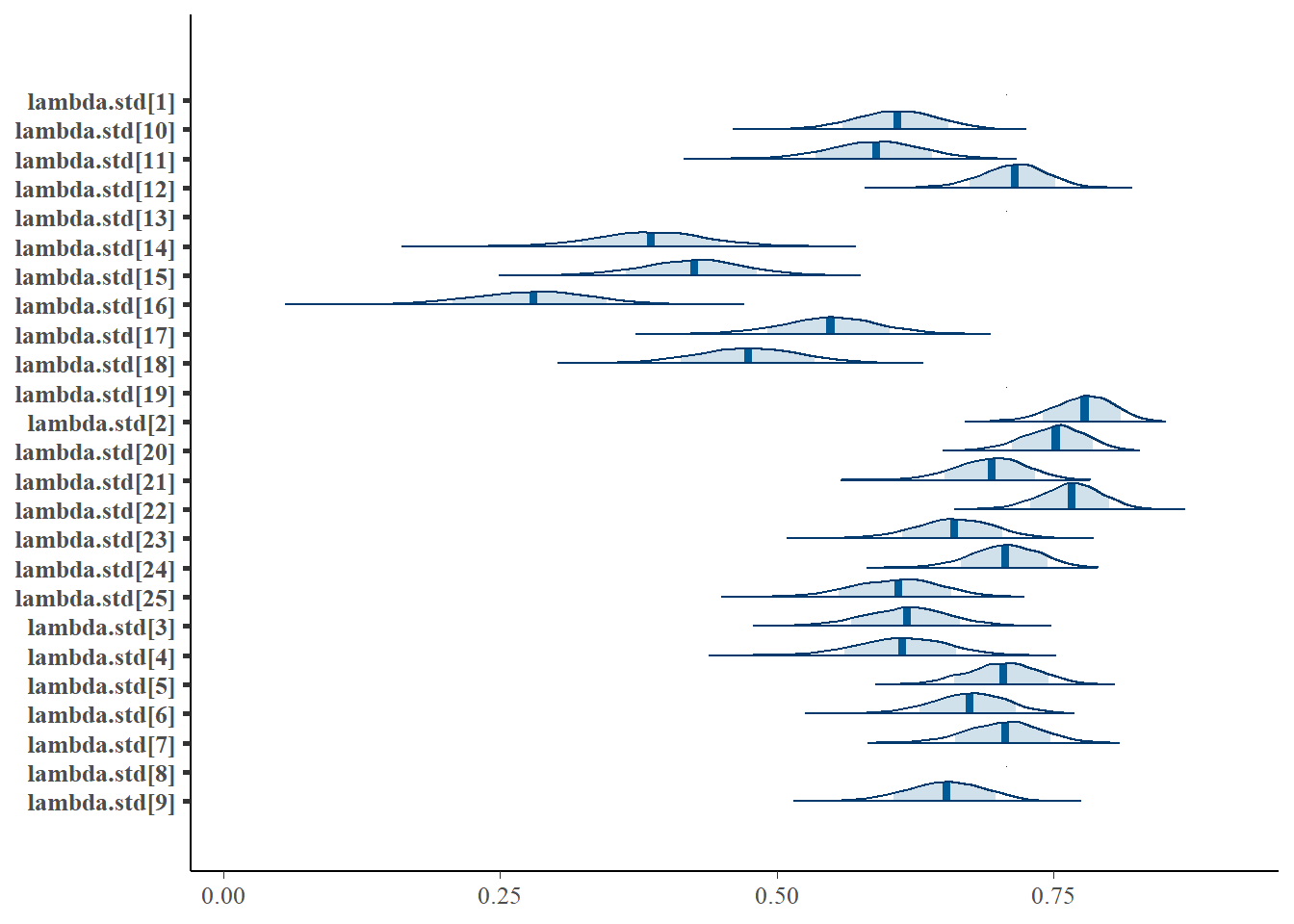
Saving 7 x 5 in imagebayesplot::mcmc_acf(fit.mcmc, regex_pars = "lambda.std"); ggsave("fig/pools_model1_lambda_acf.pdf")Warning: Removed 336 rows containing missing values (geom_segment).Warning: Removed 21 row(s) containing missing values (geom_path).
Saving 7 x 5 in imageWarning: Removed 336 rows containing missing values (geom_segment).
Warning: Removed 21 row(s) containing missing values (geom_path).bayesplot::mcmc_trace(fit.mcmc, regex_pars = "lambda.std"); ggsave("fig/pools_model1_lambda_trace.pdf")
Saving 7 x 5 in imageggmcmc::ggs_grb(fit.mcmc.ggs, family = "lambda.std"); ggsave("fig/pools_model1_lambda_grb.pdf")Warning: Removed 50 row(s) containing missing values (geom_path).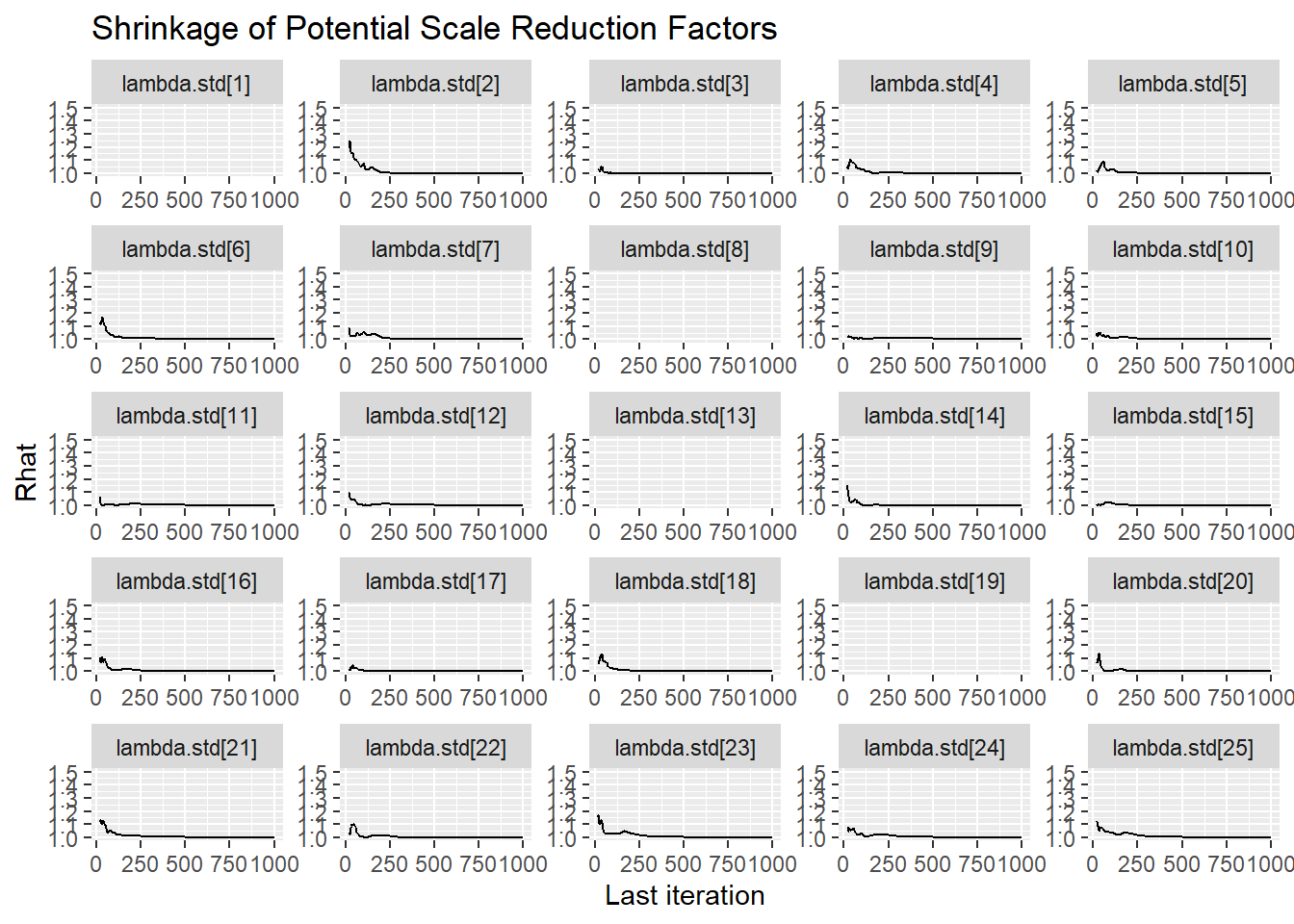
Saving 7 x 5 in imageWarning: Removed 50 row(s) containing missing values (geom_path).Factor Correlations
bayesplot::mcmc_areas(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'), prob = 0.8)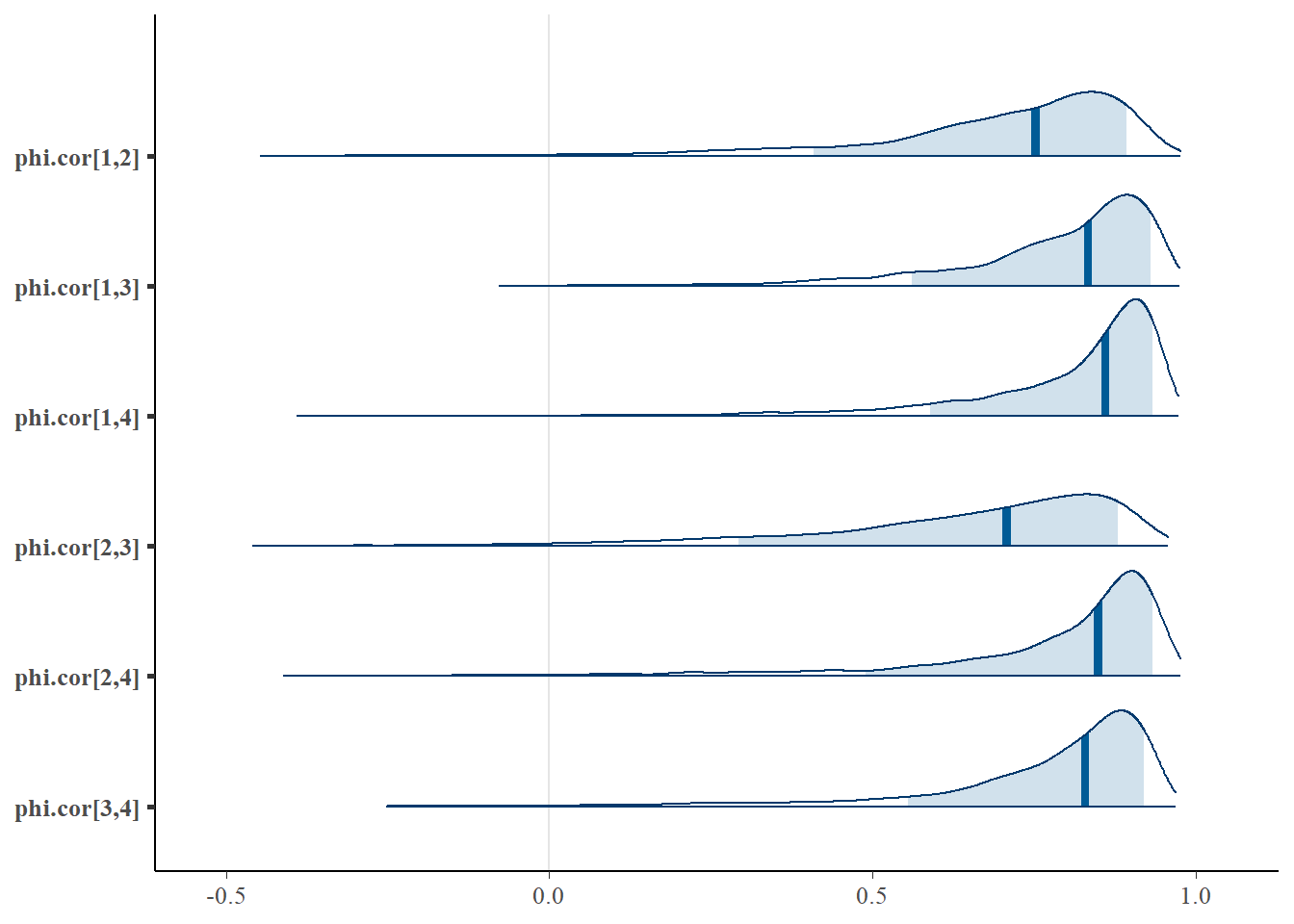
bayesplot::mcmc_acf(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'))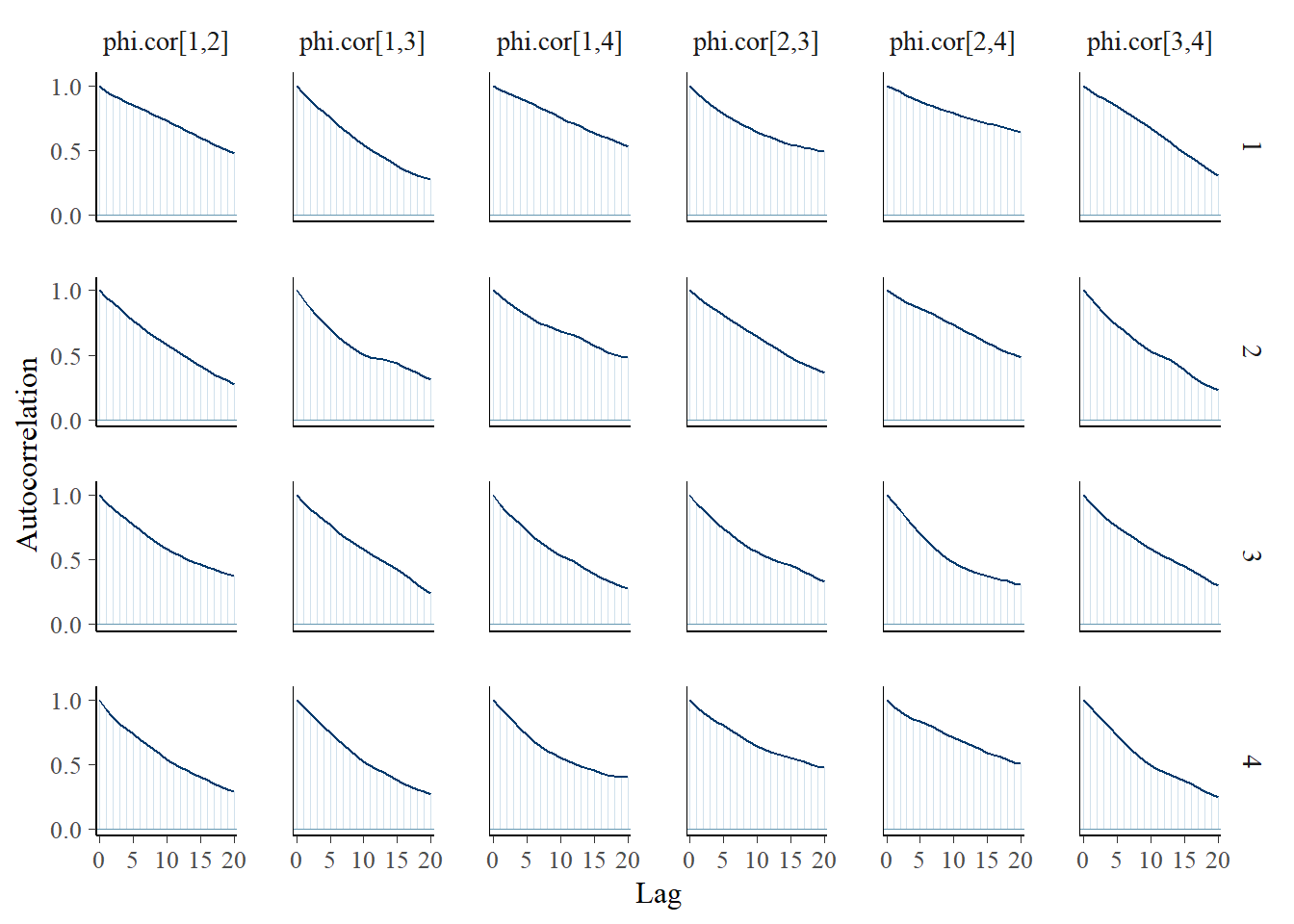
bayesplot::mcmc_trace(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'))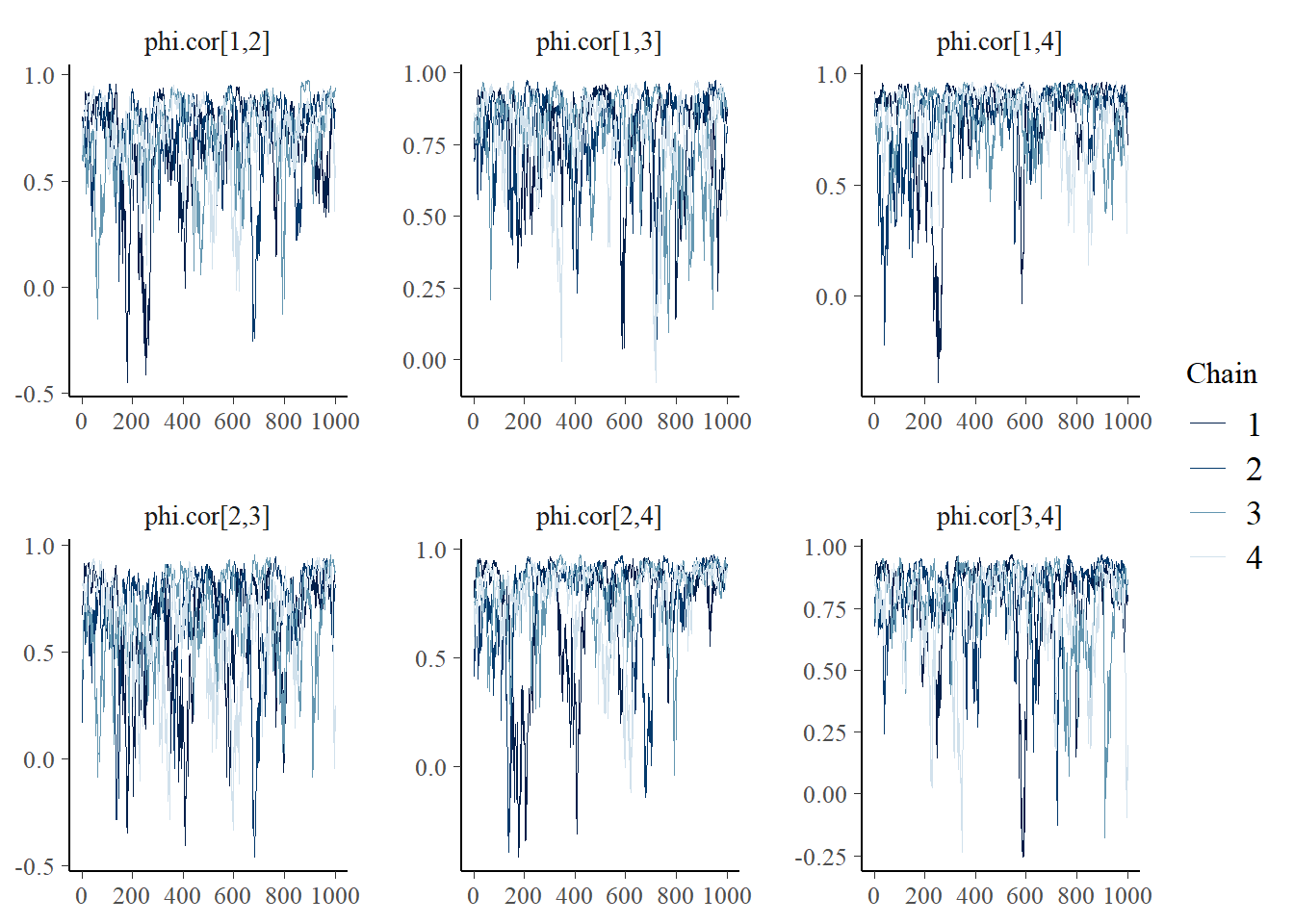
ggmcmc::ggs_grb(fit.mcmc.ggs, family = "phi.cor")Warning: Removed 50 row(s) containing missing values (geom_path).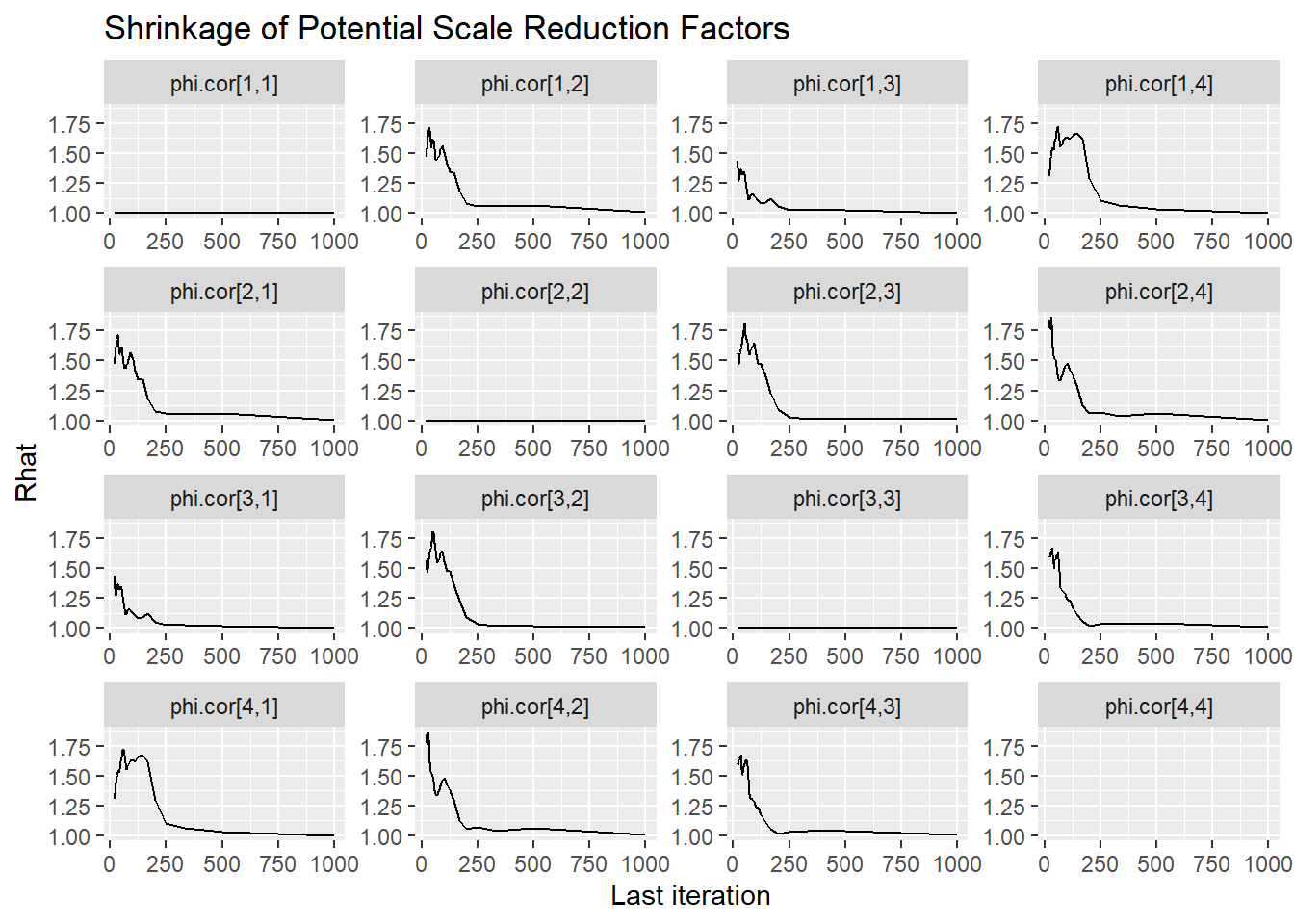
# save factor correlations
use.vars <- c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]')
extracted_cor <- fit.mcmc[,use.vars]
write.csv(x=extracted_cor, file=paste0(getwd(),"/data/pools/extracted_cor_m1.csv"))Factor Reliability Omega (\(\omega\))
bayesplot::mcmc_areas(fit.mcmc, regex_pars = "reli.omega", prob = 0.8); ggsave("fig/pools_model1_omega_dens.pdf")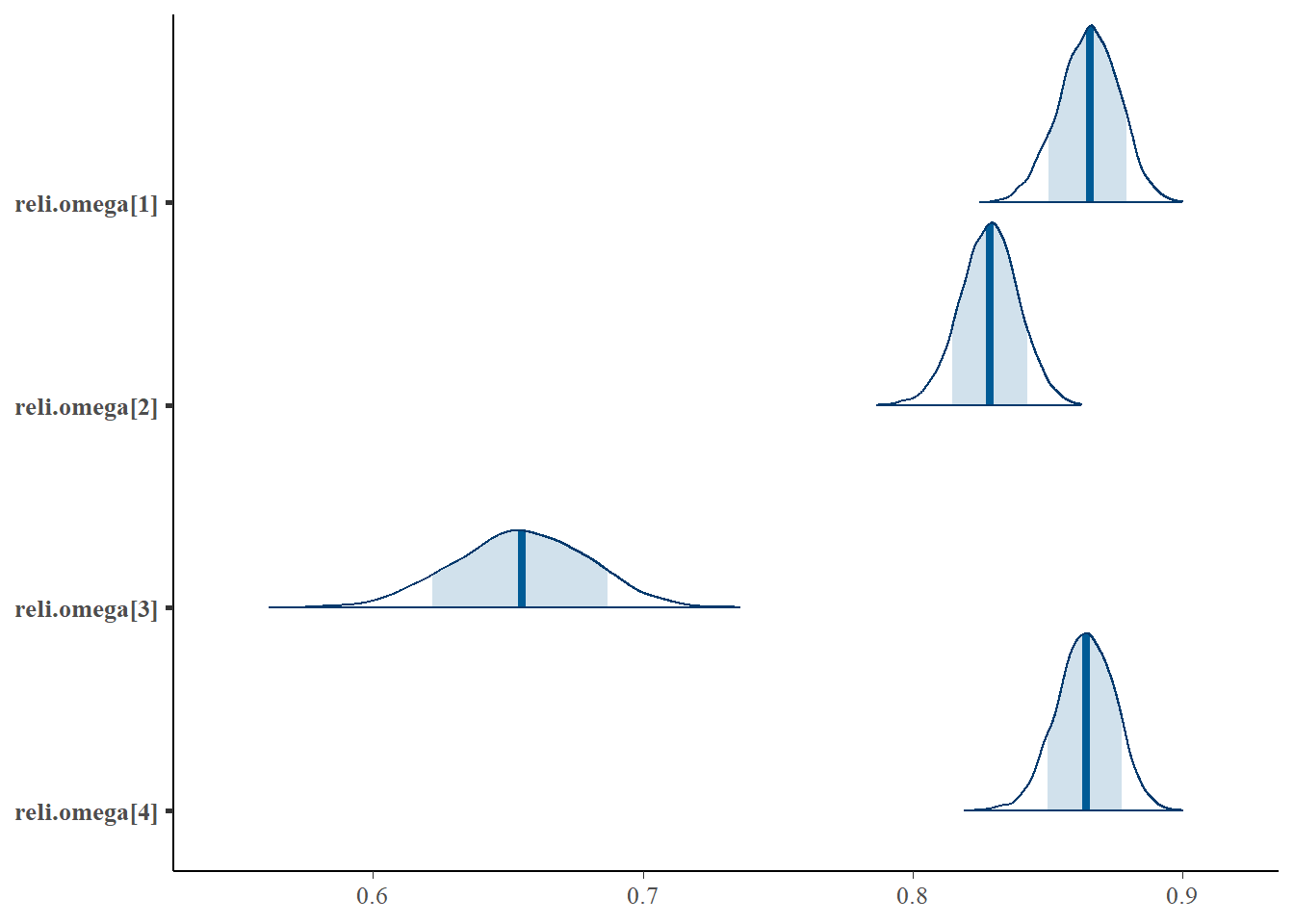
Saving 7 x 5 in imagebayesplot::mcmc_acf(fit.mcmc, regex_pars = "reli.omega"); ggsave("fig/pools_model1_omega_acf.pdf")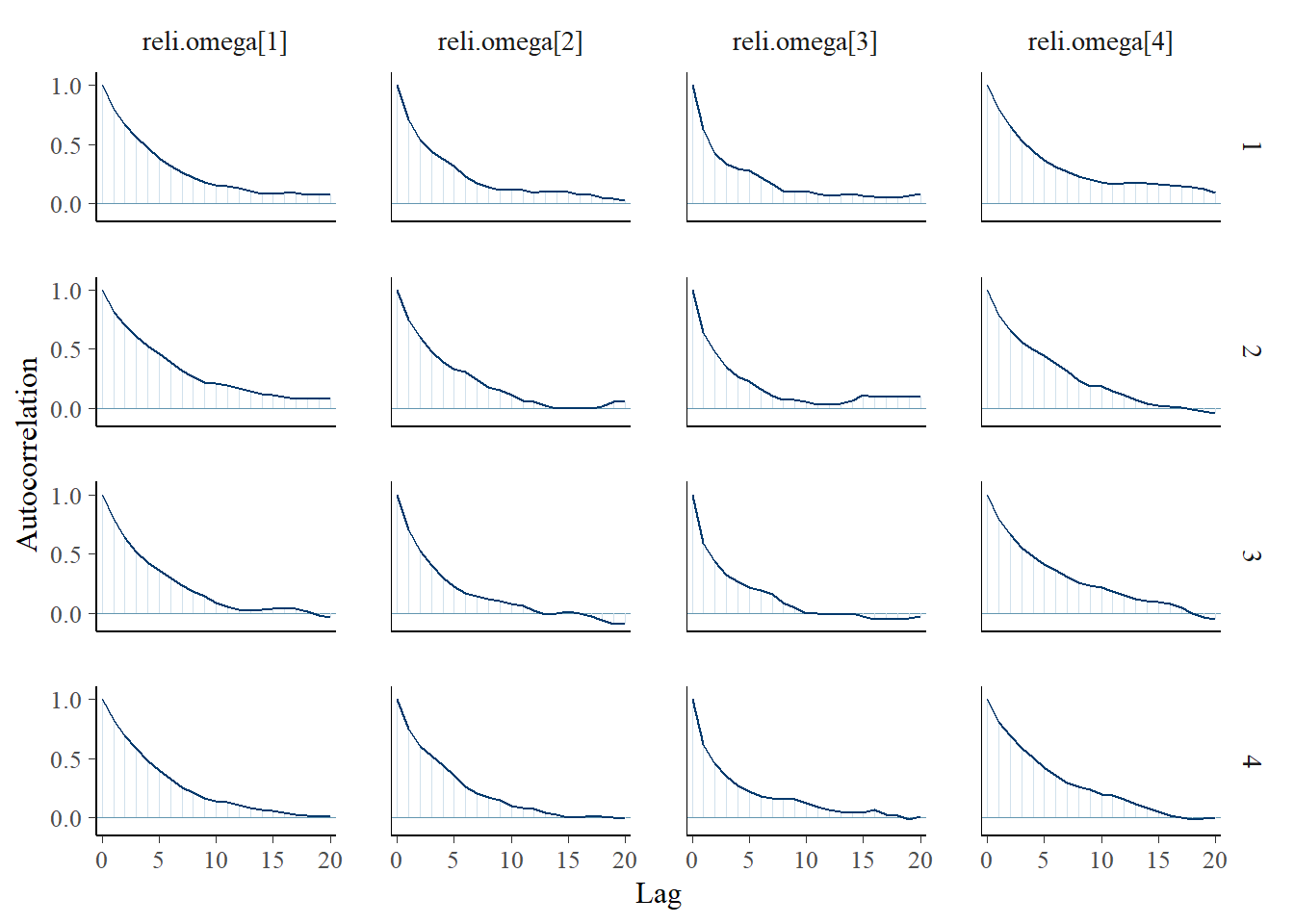
Saving 7 x 5 in imagebayesplot::mcmc_trace(fit.mcmc, regex_pars = "reli.omega"); ggsave("fig/pools_model1_omega_trace.pdf")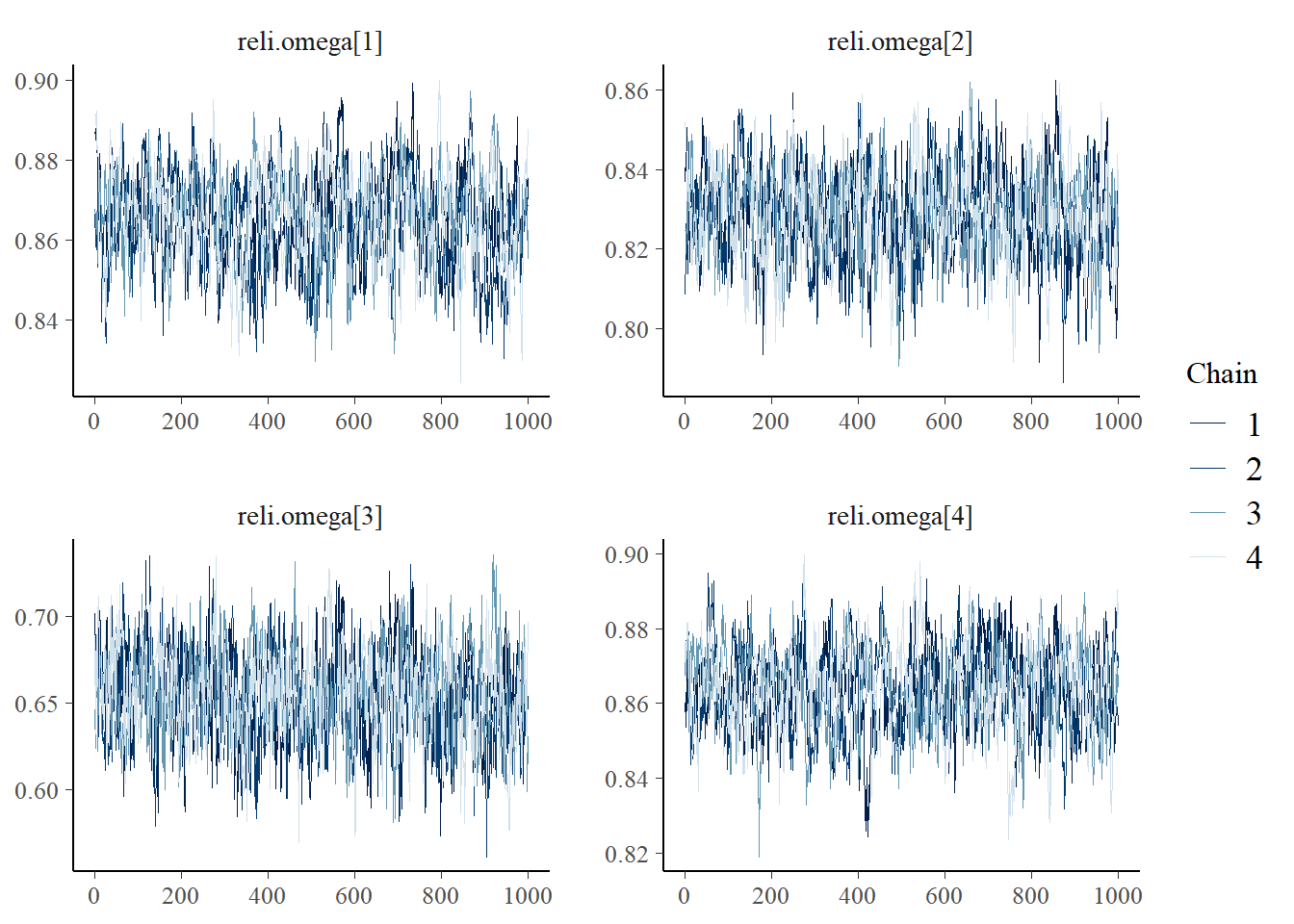
Saving 7 x 5 in imageggmcmc::ggs_grb(fit.mcmc.ggs, family = "reli.omega"); ggsave("fig/pools_model1_omega_grb.pdf")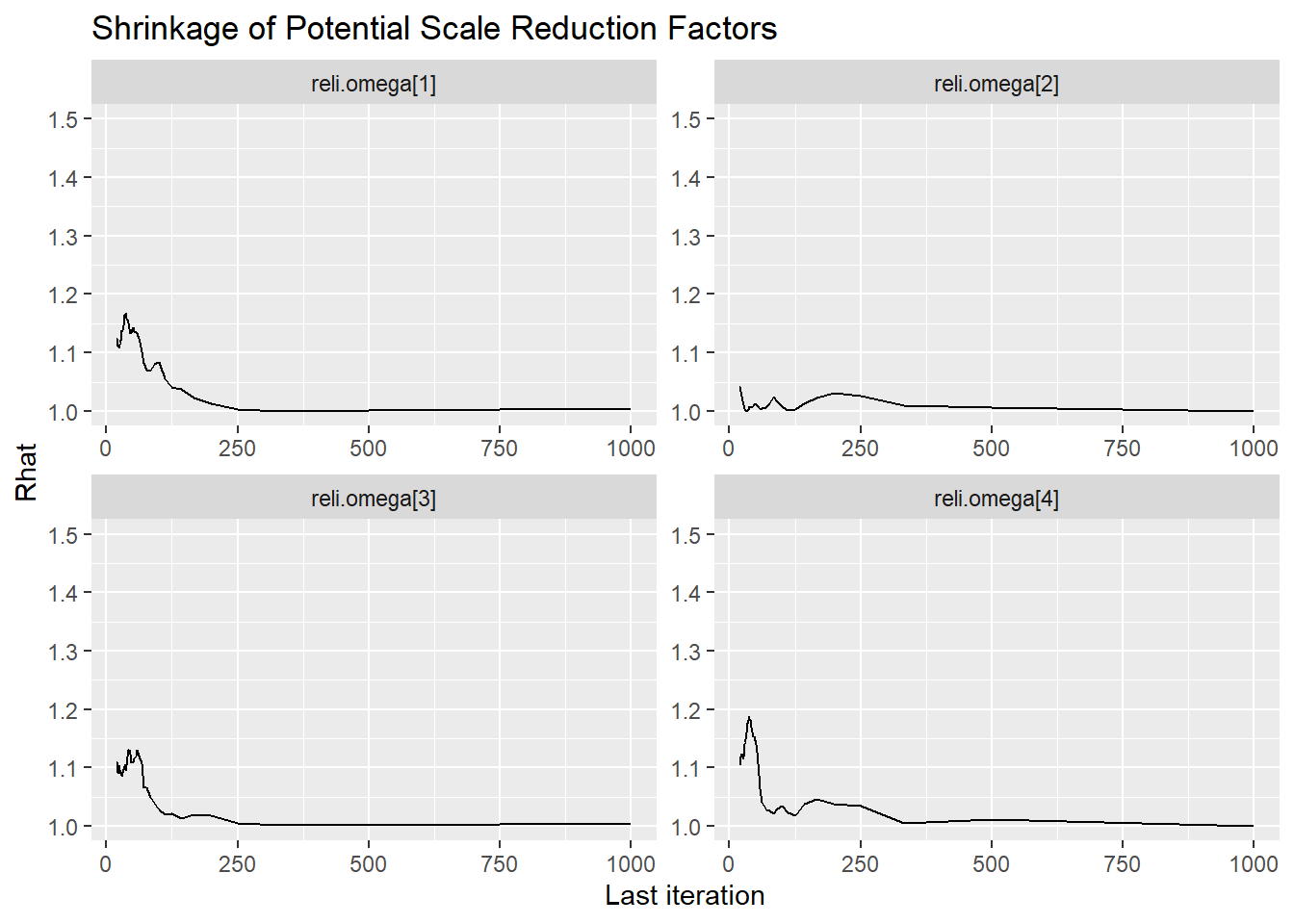
Saving 7 x 5 in image# extract omega posterior for results comparison
extracted_omega <- data.frame(model_1_f1 = fit.mcmc$`reli.omega[1]`,
model_1_f2 = fit.mcmc$`reli.omega[2]`,
model_1_f3 = fit.mcmc$`reli.omega[3]`,
model_1_f4 = fit.mcmc$`reli.omega[4]`)
write.csv(x=extracted_omega, file=paste0(getwd(),"/data/pools/extracted_omega_m1.csv"))Manuscript Table and Figures
Table
# print to xtable
print(
xtable(
model.fit$BUGSoutput$summary,
caption = c("pools Model 1 posterior distribution summary")
,align = "lrrrrrrrrr"
),
include.rownames=T,
booktabs=T
)% latex table generated in R 4.0.5 by xtable 1.8-4 package
% Wed Feb 02 04:13:56 2022
\begin{table}[ht]
\centering
\begin{tabular}{lrrrrrrrrr}
\toprule
& mean & sd & 2.5\% & 25\% & 50\% & 75\% & 97.5\% & Rhat & n.eff \\
\midrule
deviance & 15091.74 & 119.05 & 14858.10 & 15012.53 & 15091.66 & 15170.14 & 15327.72 & 1.00 & 4000.00 \\
inv.phi[1,1] & 3.16 & 1.61 & 0.76 & 2.01 & 2.90 & 4.00 & 7.17 & 1.03 & 140.00 \\
inv.phi[2,1] & -0.46 & 1.06 & -2.76 & -1.06 & -0.41 & 0.22 & 1.51 & 1.02 & 160.00 \\
inv.phi[3,1] & -1.25 & 1.10 & -3.85 & -1.85 & -1.12 & -0.46 & 0.49 & 1.01 & 230.00 \\
inv.phi[4,1] & -1.27 & 1.43 & -4.45 & -2.12 & -1.13 & -0.28 & 1.15 & 1.01 & 310.00 \\
inv.phi[1,2] & -0.46 & 1.06 & -2.76 & -1.06 & -0.41 & 0.22 & 1.51 & 1.02 & 160.00 \\
inv.phi[2,2] & 2.87 & 1.46 & 0.89 & 1.78 & 2.59 & 3.68 & 6.31 & 1.01 & 250.00 \\
inv.phi[3,2] & -0.13 & 0.90 & -1.98 & -0.68 & -0.11 & 0.42 & 1.69 & 1.01 & 490.00 \\
inv.phi[4,2] & -1.77 & 1.41 & -4.95 & -2.55 & -1.57 & -0.79 & 0.50 & 1.02 & 180.00 \\
inv.phi[1,3] & -1.25 & 1.10 & -3.85 & -1.85 & -1.12 & -0.46 & 0.49 & 1.01 & 230.00 \\
inv.phi[2,3] & -0.13 & 0.90 & -1.98 & -0.68 & -0.11 & 0.42 & 1.69 & 1.01 & 490.00 \\
inv.phi[3,3] & 2.75 & 1.32 & 0.72 & 1.80 & 2.51 & 3.47 & 5.95 & 1.02 & 180.00 \\
inv.phi[4,3] & -1.00 & 1.14 & -3.50 & -1.67 & -0.89 & -0.23 & 0.91 & 1.01 & 280.00 \\
inv.phi[1,4] & -1.27 & 1.43 & -4.45 & -2.12 & -1.13 & -0.28 & 1.15 & 1.01 & 310.00 \\
inv.phi[2,4] & -1.77 & 1.41 & -4.95 & -2.55 & -1.57 & -0.79 & 0.50 & 1.02 & 180.00 \\
inv.phi[3,4] & -1.00 & 1.14 & -3.50 & -1.67 & -0.89 & -0.23 & 0.91 & 1.01 & 280.00 \\
inv.phi[4,4] & 4.02 & 2.10 & 0.99 & 2.44 & 3.66 & 5.17 & 9.06 & 1.03 & 130.00 \\
lambda[1] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[2] & 1.24 & 0.11 & 1.03 & 1.16 & 1.24 & 1.31 & 1.46 & 1.00 & 1600.00 \\
lambda[3] & 0.79 & 0.08 & 0.64 & 0.73 & 0.79 & 0.84 & 0.96 & 1.00 & 1500.00 \\
lambda[4] & 0.78 & 0.08 & 0.63 & 0.72 & 0.78 & 0.84 & 0.95 & 1.00 & 1100.00 \\
lambda[5] & 1.00 & 0.09 & 0.83 & 0.93 & 0.99 & 1.06 & 1.19 & 1.00 & 660.00 \\
lambda[6] & 0.92 & 0.09 & 0.76 & 0.86 & 0.91 & 0.97 & 1.09 & 1.00 & 1500.00 \\
lambda[7] & 1.00 & 0.09 & 0.82 & 0.93 & 1.00 & 1.06 & 1.20 & 1.01 & 380.00 \\
lambda[8] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[9] & 0.86 & 0.08 & 0.71 & 0.81 & 0.86 & 0.92 & 1.03 & 1.00 & 900.00 \\
lambda[10] & 0.77 & 0.08 & 0.63 & 0.72 & 0.77 & 0.82 & 0.92 & 1.00 & 1500.00 \\
lambda[11] & 0.73 & 0.08 & 0.59 & 0.68 & 0.73 & 0.78 & 0.89 & 1.00 & 3000.00 \\
lambda[12] & 1.03 & 0.09 & 0.86 & 0.97 & 1.02 & 1.08 & 1.20 & 1.00 & 3900.00 \\
lambda[13] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[14] & 0.42 & 0.06 & 0.30 & 0.38 & 0.42 & 0.46 & 0.55 & 1.00 & 1300.00 \\
lambda[15] & 0.47 & 0.06 & 0.35 & 0.43 & 0.47 & 0.51 & 0.60 & 1.00 & 1300.00 \\
lambda[16] & 0.29 & 0.06 & 0.17 & 0.25 & 0.29 & 0.33 & 0.42 & 1.00 & 2100.00 \\
lambda[17] & 0.66 & 0.07 & 0.52 & 0.61 & 0.66 & 0.71 & 0.81 & 1.01 & 560.00 \\
lambda[18] & 0.54 & 0.07 & 0.41 & 0.49 & 0.54 & 0.59 & 0.69 & 1.00 & 840.00 \\
lambda[19] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[20] & 1.14 & 0.10 & 0.96 & 1.07 & 1.14 & 1.21 & 1.34 & 1.00 & 1400.00 \\
lambda[21] & 0.97 & 0.09 & 0.80 & 0.91 & 0.97 & 1.02 & 1.14 & 1.00 & 2400.00 \\
lambda[22] & 1.20 & 0.10 & 1.01 & 1.13 & 1.19 & 1.26 & 1.41 & 1.00 & 1200.00 \\
lambda[23] & 0.88 & 0.09 & 0.72 & 0.83 & 0.88 & 0.94 & 1.06 & 1.00 & 1700.00 \\
lambda[24] & 1.00 & 0.09 & 0.84 & 0.94 & 1.00 & 1.06 & 1.18 & 1.00 & 1600.00 \\
lambda[25] & 0.77 & 0.08 & 0.62 & 0.71 & 0.77 & 0.82 & 0.93 & 1.00 & 640.00 \\
lambda.std[1] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[2] & 0.78 & 0.03 & 0.72 & 0.76 & 0.78 & 0.80 & 0.83 & 1.00 & 1900.00 \\
lambda.std[3] & 0.62 & 0.04 & 0.54 & 0.59 & 0.62 & 0.64 & 0.69 & 1.00 & 1500.00 \\
lambda.std[4] & 0.61 & 0.04 & 0.53 & 0.59 & 0.61 & 0.64 & 0.69 & 1.00 & 1100.00 \\
lambda.std[5] & 0.70 & 0.03 & 0.64 & 0.68 & 0.71 & 0.73 & 0.76 & 1.00 & 690.00 \\
lambda.std[6] & 0.67 & 0.03 & 0.60 & 0.65 & 0.67 & 0.70 & 0.74 & 1.00 & 1400.00 \\
lambda.std[7] & 0.70 & 0.03 & 0.64 & 0.68 & 0.71 & 0.73 & 0.77 & 1.01 & 370.00 \\
lambda.std[8] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[9] & 0.65 & 0.04 & 0.58 & 0.63 & 0.65 & 0.68 & 0.72 & 1.00 & 830.00 \\
lambda.std[10] & 0.61 & 0.04 & 0.53 & 0.58 & 0.61 & 0.63 & 0.68 & 1.00 & 1500.00 \\
lambda.std[11] & 0.59 & 0.04 & 0.51 & 0.56 & 0.59 & 0.62 & 0.67 & 1.00 & 3100.00 \\
lambda.std[12] & 0.71 & 0.03 & 0.65 & 0.69 & 0.72 & 0.73 & 0.77 & 1.00 & 3600.00 \\
lambda.std[13] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[14] & 0.39 & 0.05 & 0.29 & 0.35 & 0.39 & 0.42 & 0.48 & 1.00 & 1400.00 \\
lambda.std[15] & 0.42 & 0.05 & 0.33 & 0.39 & 0.43 & 0.45 & 0.51 & 1.00 & 1300.00 \\
lambda.std[16] & 0.28 & 0.05 & 0.17 & 0.24 & 0.28 & 0.32 & 0.38 & 1.00 & 2100.00 \\
lambda.std[17] & 0.55 & 0.04 & 0.46 & 0.52 & 0.55 & 0.58 & 0.63 & 1.01 & 550.00 \\
lambda.std[18] & 0.47 & 0.05 & 0.38 & 0.44 & 0.47 & 0.51 & 0.57 & 1.00 & 860.00 \\
lambda.std[19] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[20] & 0.75 & 0.03 & 0.69 & 0.73 & 0.75 & 0.77 & 0.80 & 1.00 & 1300.00 \\
lambda.std[21] & 0.69 & 0.03 & 0.63 & 0.67 & 0.69 & 0.71 & 0.75 & 1.00 & 2800.00 \\
lambda.std[22] & 0.77 & 0.03 & 0.71 & 0.75 & 0.77 & 0.78 & 0.82 & 1.00 & 1100.00 \\
lambda.std[23] & 0.66 & 0.04 & 0.58 & 0.64 & 0.66 & 0.68 & 0.73 & 1.00 & 1800.00 \\
lambda.std[24] & 0.71 & 0.03 & 0.64 & 0.69 & 0.71 & 0.73 & 0.76 & 1.00 & 1700.00 \\
lambda.std[25] & 0.61 & 0.04 & 0.53 & 0.58 & 0.61 & 0.64 & 0.68 & 1.00 & 660.00 \\
phi[1,1] & 2.62 & 1.63 & 0.86 & 1.64 & 2.25 & 3.05 & 7.22 & 1.03 & 170.00 \\
phi[2,1] & 1.58 & 0.88 & 0.19 & 1.01 & 1.51 & 2.04 & 3.64 & 1.03 & 1800.00 \\
phi[3,1] & 1.93 & 1.05 & 0.46 & 1.23 & 1.77 & 2.38 & 4.55 & 1.02 & 490.00 \\
phi[4,1] & 1.91 & 0.74 & 0.53 & 1.46 & 1.90 & 2.32 & 3.47 & 1.03 & 360.00 \\
phi[1,2] & 1.58 & 0.88 & 0.19 & 1.01 & 1.51 & 2.04 & 3.64 & 1.03 & 1800.00 \\
phi[2,2] & 2.08 & 1.02 & 0.72 & 1.37 & 1.90 & 2.52 & 4.72 & 1.02 & 280.00 \\
phi[3,2] & 1.40 & 0.82 & 0.03 & 0.84 & 1.31 & 1.88 & 3.14 & 1.02 & 200.00 \\
phi[4,2] & 1.68 & 0.70 & 0.19 & 1.26 & 1.71 & 2.12 & 3.06 & 1.02 & 270.00 \\
phi[1,3] & 1.93 & 1.05 & 0.46 & 1.23 & 1.77 & 2.38 & 4.55 & 1.02 & 490.00 \\
phi[2,3] & 1.40 & 0.82 & 0.03 & 0.84 & 1.31 & 1.88 & 3.14 & 1.02 & 200.00 \\
phi[3,3] & 2.37 & 1.20 & 0.82 & 1.52 & 2.13 & 2.95 & 5.18 & 1.00 & 4000.00 \\
phi[4,3] & 1.78 & 0.67 & 0.43 & 1.34 & 1.78 & 2.22 & 3.07 & 1.01 & 550.00 \\
phi[1,4] & 1.91 & 0.74 & 0.53 & 1.46 & 1.90 & 2.32 & 3.47 & 1.03 & 360.00 \\
phi[2,4] & 1.68 & 0.70 & 0.19 & 1.26 & 1.71 & 2.12 & 3.06 & 1.02 & 270.00 \\
phi[3,4] & 1.78 & 0.67 & 0.43 & 1.34 & 1.78 & 2.22 & 3.07 & 1.01 & 550.00 \\
phi[4,4] & 2.29 & 0.24 & 1.86 & 2.12 & 2.28 & 2.44 & 2.81 & 1.00 & 1800.00 \\
phi.cor[1,1] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[2,1] & 0.70 & 0.21 & 0.12 & 0.62 & 0.75 & 0.84 & 0.93 & 1.03 & 200.00 \\
phi.cor[3,1] & 0.78 & 0.16 & 0.37 & 0.72 & 0.83 & 0.89 & 0.95 & 1.01 & 780.00 \\
phi.cor[4,1] & 0.80 & 0.17 & 0.32 & 0.75 & 0.86 & 0.91 & 0.95 & 1.03 & 890.00 \\
phi.cor[1,2] & 0.70 & 0.21 & 0.12 & 0.62 & 0.75 & 0.84 & 0.93 & 1.03 & 200.00 \\
phi.cor[2,2] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[3,2] & 0.64 & 0.24 & 0.02 & 0.53 & 0.71 & 0.82 & 0.91 & 1.02 & 170.00 \\
phi.cor[4,2] & 0.77 & 0.22 & 0.11 & 0.72 & 0.85 & 0.90 & 0.95 & 1.05 & 210.00 \\
phi.cor[1,3] & 0.78 & 0.16 & 0.37 & 0.72 & 0.83 & 0.89 & 0.95 & 1.01 & 780.00 \\
phi.cor[2,3] & 0.64 & 0.24 & 0.02 & 0.53 & 0.71 & 0.82 & 0.91 & 1.02 & 170.00 \\
phi.cor[3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[4,3] & 0.77 & 0.18 & 0.24 & 0.72 & 0.83 & 0.89 & 0.94 & 1.02 & 200.00 \\
phi.cor[1,4] & 0.80 & 0.17 & 0.32 & 0.75 & 0.86 & 0.91 & 0.95 & 1.03 & 890.00 \\
phi.cor[2,4] & 0.77 & 0.22 & 0.11 & 0.72 & 0.85 & 0.90 & 0.95 & 1.05 & 210.00 \\
phi.cor[3,4] & 0.77 & 0.18 & 0.24 & 0.72 & 0.83 & 0.89 & 0.94 & 1.02 & 200.00 \\
phi.cor[4,4] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
reli.omega[1] & 0.87 & 0.01 & 0.84 & 0.86 & 0.87 & 0.87 & 0.89 & 1.01 & 430.00 \\
reli.omega[2] & 0.83 & 0.01 & 0.81 & 0.82 & 0.83 & 0.84 & 0.85 & 1.00 & 4000.00 \\
reli.omega[3] & 0.65 & 0.03 & 0.60 & 0.64 & 0.66 & 0.67 & 0.70 & 1.01 & 410.00 \\
reli.omega[4] & 0.86 & 0.01 & 0.84 & 0.86 & 0.86 & 0.87 & 0.88 & 1.00 & 3100.00 \\
tau[1,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[4,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[5,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[6,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[7,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[8,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[9,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[10,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[11,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[12,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[13,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[14,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[15,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[16,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[17,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[18,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[19,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[20,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[21,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[22,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[23,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[24,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[25,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[1,2] & 2.84 & 0.15 & 2.55 & 2.74 & 2.84 & 2.94 & 3.14 & 1.00 & 3900.00 \\
tau[2,2] & 3.23 & 0.20 & 2.87 & 3.10 & 3.23 & 3.37 & 3.65 & 1.00 & 2300.00 \\
tau[3,2] & 2.35 & 0.15 & 2.06 & 2.25 & 2.35 & 2.45 & 2.65 & 1.00 & 1800.00 \\
tau[4,2] & 1.78 & 0.12 & 1.56 & 1.70 & 1.78 & 1.86 & 2.01 & 1.00 & 770.00 \\
tau[5,2] & 2.30 & 0.14 & 2.02 & 2.19 & 2.30 & 2.40 & 2.58 & 1.00 & 840.00 \\
tau[6,2] & 2.59 & 0.16 & 2.30 & 2.47 & 2.58 & 2.69 & 2.91 & 1.00 & 2700.00 \\
tau[7,2] & 3.09 & 0.20 & 2.71 & 2.95 & 3.08 & 3.22 & 3.48 & 1.00 & 1500.00 \\
tau[8,2] & 1.90 & 0.11 & 1.69 & 1.83 & 1.90 & 1.97 & 2.11 & 1.00 & 4000.00 \\
tau[9,2] & 1.10 & 0.08 & 0.94 & 1.04 & 1.09 & 1.15 & 1.26 & 1.00 & 1200.00 \\
tau[10,2] & 1.44 & 0.10 & 1.25 & 1.37 & 1.44 & 1.50 & 1.64 & 1.00 & 4000.00 \\
tau[11,2] & 0.67 & 0.05 & 0.56 & 0.63 & 0.66 & 0.70 & 0.78 & 1.00 & 3100.00 \\
tau[12,2] & 1.70 & 0.10 & 1.50 & 1.63 & 1.70 & 1.76 & 1.90 & 1.00 & 3300.00 \\
tau[13,2] & 1.68 & 0.09 & 1.50 & 1.61 & 1.68 & 1.74 & 1.86 & 1.00 & 1500.00 \\
tau[14,2] & 1.64 & 0.13 & 1.38 & 1.55 & 1.64 & 1.72 & 1.90 & 1.00 & 1000.00 \\
tau[15,2] & 1.27 & 0.09 & 1.10 & 1.21 & 1.27 & 1.34 & 1.46 & 1.00 & 2500.00 \\
tau[16,2] & 1.84 & 0.18 & 1.49 & 1.71 & 1.83 & 1.96 & 2.21 & 1.00 & 4000.00 \\
tau[17,2] & 2.21 & 0.16 & 1.91 & 2.10 & 2.21 & 2.31 & 2.52 & 1.00 & 720.00 \\
tau[18,2] & 2.09 & 0.15 & 1.80 & 1.99 & 2.09 & 2.19 & 2.39 & 1.00 & 1400.00 \\
tau[19,2] & 1.95 & 0.10 & 1.77 & 1.88 & 1.95 & 2.02 & 2.15 & 1.00 & 2000.00 \\
tau[20,2] & 2.64 & 0.15 & 2.35 & 2.54 & 2.64 & 2.75 & 2.95 & 1.00 & 1300.00 \\
tau[21,2] & 1.65 & 0.10 & 1.45 & 1.58 & 1.65 & 1.72 & 1.85 & 1.00 & 700.00 \\
tau[22,2] & 2.03 & 0.12 & 1.80 & 1.95 & 2.03 & 2.12 & 2.28 & 1.00 & 700.00 \\
tau[23,2] & 0.58 & 0.05 & 0.49 & 0.55 & 0.58 & 0.62 & 0.69 & 1.00 & 4000.00 \\
tau[24,2] & 1.91 & 0.11 & 1.70 & 1.83 & 1.90 & 1.98 & 2.13 & 1.00 & 1000.00 \\
tau[25,2] & 0.75 & 0.06 & 0.64 & 0.71 & 0.74 & 0.78 & 0.86 & 1.00 & 2300.00 \\
theta[1] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[2] & 2.55 & 0.27 & 2.07 & 2.36 & 2.54 & 2.73 & 3.13 & 1.00 & 1400.00 \\
theta[3] & 1.63 & 0.13 & 1.41 & 1.54 & 1.62 & 1.70 & 1.91 & 1.00 & 1500.00 \\
theta[4] & 1.62 & 0.13 & 1.40 & 1.52 & 1.60 & 1.70 & 1.89 & 1.00 & 1300.00 \\
theta[5] & 2.00 & 0.19 & 1.69 & 1.87 & 1.99 & 2.12 & 2.40 & 1.00 & 630.00 \\
theta[6] & 1.85 & 0.16 & 1.57 & 1.74 & 1.84 & 1.95 & 2.20 & 1.00 & 1600.00 \\
theta[7] & 2.01 & 0.19 & 1.68 & 1.87 & 1.99 & 2.13 & 2.43 & 1.01 & 390.00 \\
theta[8] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[9] & 1.75 & 0.14 & 1.50 & 1.65 & 1.74 & 1.85 & 2.06 & 1.00 & 1000.00 \\
theta[10] & 1.60 & 0.12 & 1.40 & 1.51 & 1.59 & 1.67 & 1.85 & 1.00 & 1500.00 \\
theta[11] & 1.54 & 0.12 & 1.34 & 1.46 & 1.53 & 1.61 & 1.80 & 1.00 & 2900.00 \\
theta[12] & 2.06 & 0.18 & 1.73 & 1.93 & 2.05 & 2.17 & 2.45 & 1.00 & 4000.00 \\
theta[13] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[14] & 1.18 & 0.05 & 1.09 & 1.14 & 1.18 & 1.21 & 1.30 & 1.00 & 1300.00 \\
theta[15] & 1.23 & 0.06 & 1.12 & 1.18 & 1.22 & 1.26 & 1.36 & 1.00 & 1500.00 \\
theta[16] & 1.09 & 0.04 & 1.03 & 1.06 & 1.09 & 1.11 & 1.17 & 1.00 & 3100.00 \\
theta[17] & 1.44 & 0.10 & 1.27 & 1.37 & 1.43 & 1.50 & 1.66 & 1.00 & 580.00 \\
theta[18] & 1.30 & 0.08 & 1.17 & 1.24 & 1.29 & 1.34 & 1.47 & 1.00 & 810.00 \\
theta[19] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[20] & 2.31 & 0.23 & 1.91 & 2.15 & 2.30 & 2.46 & 2.80 & 1.00 & 1500.00 \\
theta[21] & 1.94 & 0.17 & 1.65 & 1.82 & 1.93 & 2.04 & 2.30 & 1.00 & 2100.00 \\
theta[22] & 2.44 & 0.25 & 2.01 & 2.27 & 2.42 & 2.60 & 2.99 & 1.00 & 1300.00 \\
theta[23] & 1.79 & 0.16 & 1.52 & 1.68 & 1.77 & 1.88 & 2.13 & 1.00 & 1500.00 \\
theta[24] & 2.01 & 0.17 & 1.70 & 1.89 & 2.00 & 2.12 & 2.38 & 1.00 & 1500.00 \\
theta[25] & 1.60 & 0.12 & 1.39 & 1.51 & 1.59 & 1.68 & 1.86 & 1.00 & 610.00 \\
\bottomrule
\end{tabular}
\caption{pools Model 1 posterior distribution summary}
\end{table}
sessionInfo()R version 4.0.5 (2021-03-31)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 22000)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.1252
[2] LC_CTYPE=English_United States.1252
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] readxl_1.3.1 car_3.0-10 carData_3.0-4
[4] mvtnorm_1.1-1 LaplacesDemon_16.1.4 runjags_2.2.0-2
[7] lme4_1.1-26 Matrix_1.3-2 sirt_3.9-4
[10] R2jags_0.6-1 rjags_4-12 eRm_1.0-2
[13] diffIRT_1.5 statmod_1.4.35 xtable_1.8-4
[16] kableExtra_1.3.4 lavaan_0.6-7 polycor_0.7-10
[19] bayesplot_1.8.0 ggmcmc_1.5.1.1 coda_0.19-4
[22] data.table_1.14.0 patchwork_1.1.1 forcats_0.5.1
[25] stringr_1.4.0 dplyr_1.0.5 purrr_0.3.4
[28] readr_1.4.0 tidyr_1.1.3 tibble_3.1.0
[31] ggplot2_3.3.5 tidyverse_1.3.0 workflowr_1.6.2
loaded via a namespace (and not attached):
[1] minqa_1.2.4 TAM_3.5-19 colorspace_2.0-0 rio_0.5.26
[5] ellipsis_0.3.1 ggridges_0.5.3 rprojroot_2.0.2 fs_1.5.0
[9] rstudioapi_0.13 farver_2.1.0 fansi_0.4.2 lubridate_1.7.10
[13] xml2_1.3.2 splines_4.0.5 mnormt_2.0.2 knitr_1.31
[17] jsonlite_1.7.2 nloptr_1.2.2.2 broom_0.7.5 dbplyr_2.1.0
[21] compiler_4.0.5 httr_1.4.2 backports_1.2.1 assertthat_0.2.1
[25] cli_2.3.1 later_1.1.0.1 htmltools_0.5.1.1 tools_4.0.5
[29] gtable_0.3.0 glue_1.4.2 reshape2_1.4.4 Rcpp_1.0.7
[33] cellranger_1.1.0 jquerylib_0.1.3 vctrs_0.3.6 svglite_2.0.0
[37] nlme_3.1-152 psych_2.0.12 xfun_0.21 ps_1.6.0
[41] openxlsx_4.2.3 rvest_1.0.0 lifecycle_1.0.0 MASS_7.3-53.1
[45] scales_1.1.1 ragg_1.1.1 hms_1.0.0 promises_1.2.0.1
[49] parallel_4.0.5 RColorBrewer_1.1-2 curl_4.3 yaml_2.2.1
[53] sass_0.3.1 reshape_0.8.8 stringi_1.5.3 highr_0.8
[57] zip_2.1.1 boot_1.3-27 rlang_0.4.10 pkgconfig_2.0.3
[61] systemfonts_1.0.1 evaluate_0.14 lattice_0.20-41 labeling_0.4.2
[65] tidyselect_1.1.0 GGally_2.1.1 plyr_1.8.6 magrittr_2.0.1
[69] R6_2.5.0 generics_0.1.0 DBI_1.1.1 foreign_0.8-81
[73] pillar_1.5.1 haven_2.3.1 withr_2.4.1 abind_1.4-5
[77] modelr_0.1.8 crayon_1.4.1 utf8_1.1.4 tmvnsim_1.0-2
[81] rmarkdown_2.7 grid_4.0.5 CDM_7.5-15 pbivnorm_0.6.0
[85] git2r_0.28.0 reprex_1.0.0 digest_0.6.27 webshot_0.5.2
[89] httpuv_1.5.5 textshaping_0.3.1 stats4_4.0.5 munsell_0.5.0
[93] viridisLite_0.3.0 bslib_0.2.4 R2WinBUGS_2.1-21