SERA POOLS Study
Model 3 Results
R. Noah Padgett
2022-02-01
Last updated: 2022-02-02
Checks: 4 2
Knit directory: Padgett-Dissertation/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity itโs best to always run the code in an empty environment.
The command set.seed(20210401) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
The following chunks had caches available:
- model3
To ensure reproducibility of the results, delete the cache directory pools_model3_results_cache and re-run the analysis. To have workflowr automatically delete the cache directory prior to building the file, set delete_cache = TRUE when running wflow_build() or wflow_publish().
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Tracking code development and connecting the code version to the results is critical for reproducibility. To start using Git, open the Terminal and type git init in your project directory.
This project is not being versioned with Git. To obtain the full reproducibility benefits of using workflowr, please see ?wflow_start.
# Load packages & utility functions
source("code/load_packages.R")
source("code/load_utility_functions.R")
# environment options
options(scipen = 999, digits=3)POOLS Data
library(readxl)
mydata <- read_excel("data/pools/POOLS_data_2020-11-16.xlsx")
use.var <- c(paste0("Q4_",c(3:5,9,11,15,18)),
paste0("Q5_",c(1:3,5:6,12)),
paste0("Q6_",c(2,5:8, 11)),
paste0("Q7_",c(2, 4:5, 7:8, 14)))
# trichotomize
f <- function(x){
y=numeric(length(x))
for(i in 1:length(x)){
if(x[i] < 3){
y[i] = 1
}
if(x[i] == 3){
y[i] = 2
}
if(x[i] > 3){
y[i] = 3
}
}
return(y)
}
mydata <- na.omit(mydata[, use.var])
mydata <- apply(mydata, 2, f) %>%
as.data.frame()
psych::describe(
mydata
) vars n mean sd median trimmed mad min max range skew kurtosis se
Q4_3 1 490 1.62 0.65 2 1.53 1.48 1 3 2 0.57 -0.68 0.03
Q4_4 2 490 1.64 0.65 2 1.56 1.48 1 3 2 0.51 -0.71 0.03
Q4_5 3 490 1.52 0.68 1 1.40 0.00 1 3 2 0.92 -0.36 0.03
Q4_9 4 490 1.65 0.76 1 1.56 0.00 1 3 2 0.69 -0.96 0.03
Q4_11 5 490 1.64 0.72 1 1.55 0.00 1 3 2 0.66 -0.85 0.03
Q4_15 6 490 1.58 0.68 1 1.47 0.00 1 3 2 0.74 -0.59 0.03
Q4_18 7 490 1.52 0.63 1 1.43 0.00 1 3 2 0.81 -0.38 0.03
Q5_1 8 490 1.73 0.77 2 1.66 1.48 1 3 2 0.50 -1.16 0.03
Q5_2 9 490 2.00 0.86 2 2.00 1.48 1 3 2 0.00 -1.64 0.04
Q5_3 10 490 1.79 0.81 2 1.73 1.48 1 3 2 0.41 -1.37 0.04
Q5_5 11 490 2.33 0.81 3 2.41 0.00 1 3 2 -0.67 -1.18 0.04
Q5_6 12 490 1.94 0.77 2 1.93 1.48 1 3 2 0.09 -1.33 0.03
Q5_12 13 490 1.92 0.78 2 1.90 1.48 1 3 2 0.14 -1.36 0.04
Q6_2 14 490 1.40 0.67 1 1.24 0.00 1 3 2 1.42 0.64 0.03
Q6_5 15 490 1.66 0.80 1 1.58 0.00 1 3 2 0.68 -1.11 0.04
Q6_6 16 490 1.22 0.52 1 1.09 0.00 1 3 2 2.29 4.28 0.02
Q6_7 17 490 1.45 0.66 1 1.32 0.00 1 3 2 1.17 0.14 0.03
Q6_8 18 490 1.43 0.65 1 1.31 0.00 1 3 2 1.21 0.27 0.03
Q6_11 19 490 1.85 0.76 2 1.81 1.48 1 3 2 0.26 -1.22 0.03
Q7_2 20 490 1.74 0.69 2 1.67 1.48 1 3 2 0.39 -0.89 0.03
Q7_4 21 490 1.89 0.79 2 1.86 1.48 1 3 2 0.20 -1.37 0.04
Q7_5 22 490 1.89 0.76 2 1.86 1.48 1 3 2 0.19 -1.24 0.03
Q7_7 23 490 2.43 0.78 3 2.54 0.00 1 3 2 -0.91 -0.76 0.04
Q7_8 24 490 1.87 0.75 2 1.84 1.48 1 3 2 0.21 -1.21 0.03
Q7_14 25 490 2.39 0.76 3 2.49 0.00 1 3 2 -0.78 -0.85 0.03DWLS
mod <- '
EL =~ 1*Q4_3 + lam44*Q4_4 + lam45*Q4_5 + lam49*Q4_9 + lam411*Q4_11 + lam415*Q4_15 + lam418*Q4_18
SC =~ 1*Q5_1 + lam52*Q5_2 + lam53*Q5_3 + lam55*Q5_5 + lam56*Q5_6 + lam512*Q5_12
IN =~ 1*Q6_2 + lam65*Q6_5 + lam66*Q6_6 + lam67*Q6_7 + lam68*Q6_8 + lam611*Q6_11
EN =~ 1*Q7_2 + lam74*Q7_4 + lam75*Q7_5 + lam77*Q7_7 + lam78*Q7_8 + lam714*Q7_14
# Factor covarainces
EL ~~ EL + SC + IN + EN
SC ~~ SC + IN + EN
IN ~~ IN + EN
EN ~~ EN
# Factor Reliabilities
rEL := ((1 + lam44 + lam45 + lam49 + lam411 + lam415 + lam418)**2)/((1 + lam44 + lam45 + lam49 + lam411 + lam415 + lam418)**2 + 7)
rSC := ((1 + lam52 + lam53 + lam55 + lam56 + lam512)**2)/((1 + lam52 + lam53 + lam55 + lam56 + lam512)**2 + 6)
rIN := ((1 + lam65 + lam66 + lam67 + lam68 + lam611)**2)/((1 + lam65 + lam66 + lam67 + lam68 + lam611)**2 + 6)
rEN := ((1 + lam74 + lam75 + lam77 + lam78 + lam714)**2)/((1 + lam74 + lam75 + lam77 + lam78 + lam714)**2 + 6)
'
fit.dwls <- lavaan::cfa(mod, data=mydata, ordered=T, parameterization="theta")
summary(fit.dwls, standardized=T, fit.measures=T)lavaan 0.6-7 ended normally after 66 iterations
Estimator DWLS
Optimization method NLMINB
Number of free parameters 81
Number of observations 490
Model Test User Model:
Standard Robust
Test Statistic 593.869 765.951
Degrees of freedom 269 269
P-value (Chi-square) 0.000 0.000
Scaling correction factor 0.883
Shift parameter 93.760
simple second-order correction
Model Test Baseline Model:
Test statistic 32729.962 10489.239
Degrees of freedom 300 300
P-value 0.000 0.000
Scaling correction factor 3.183
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.990 0.951
Tucker-Lewis Index (TLI) 0.989 0.946
Robust Comparative Fit Index (CFI) NA
Robust Tucker-Lewis Index (TLI) NA
Root Mean Square Error of Approximation:
RMSEA 0.050 0.061
90 Percent confidence interval - lower 0.044 0.056
90 Percent confidence interval - upper 0.055 0.067
P-value RMSEA <= 0.05 0.529 0.000
Robust RMSEA NA
90 Percent confidence interval - lower NA
90 Percent confidence interval - upper NA
Standardized Root Mean Square Residual:
SRMR 0.065 0.065
Parameter Estimates:
Standard errors Robust.sem
Information Expected
Information saturated (h1) model Unstructured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL =~
Q4_3 1.000 1.234 0.777
Q4_4 (lm44) 1.445 0.145 9.972 0.000 1.783 0.872
Q4_5 (lm45) 0.949 0.101 9.390 0.000 1.171 0.760
Q4_9 (lm49) 0.763 0.084 9.048 0.000 0.942 0.686
Q4_11 (l411) 1.048 0.110 9.536 0.000 1.293 0.791
Q4_15 (l415) 0.994 0.107 9.309 0.000 1.227 0.775
Q4_18 (l418) 1.272 0.137 9.295 0.000 1.569 0.843
SC =~
Q5_1 1.000 1.082 0.734
Q5_2 (lm52) 0.976 0.119 8.171 0.000 1.056 0.726
Q5_3 (lm53) 0.944 0.124 7.587 0.000 1.021 0.714
Q5_5 (lm55) 0.803 0.114 7.052 0.000 0.869 0.656
Q5_6 (lm56) 1.224 0.162 7.549 0.000 1.324 0.798
Q5_12 (l512) 1.188 0.160 7.446 0.000 1.286 0.789
IN =~
Q6_2 1.000 1.054 0.725
Q6_5 (lm65) 0.618 0.095 6.522 0.000 0.651 0.546
Q6_6 (lm66) 1.704 0.290 5.882 0.000 1.796 0.874
Q6_7 (lm67) 1.518 0.220 6.893 0.000 1.600 0.848
Q6_8 (lm68) 1.234 0.157 7.839 0.000 1.301 0.793
Q6_11 (l611) 1.602 0.256 6.258 0.000 1.688 0.860
EN =~
Q7_2 1.000 1.243 0.779
Q7_4 (lm74) 0.800 0.088 9.095 0.000 0.994 0.705
Q7_5 (lm75) 1.108 0.132 8.392 0.000 1.378 0.809
Q7_7 (lm77) 0.875 0.125 6.996 0.000 1.087 0.736
Q7_8 (lm78) 0.867 0.095 9.155 0.000 1.078 0.733
Q7_14 (l714) 0.672 0.088 7.626 0.000 0.835 0.641
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL ~~
SC 0.915 0.139 6.573 0.000 0.685 0.685
IN 0.973 0.152 6.402 0.000 0.748 0.748
EN 1.193 0.161 7.417 0.000 0.778 0.778
SC ~~
IN 0.740 0.129 5.718 0.000 0.649 0.649
EN 1.080 0.161 6.691 0.000 0.803 0.803
IN ~~
EN 0.979 0.156 6.265 0.000 0.747 0.747
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q4_3 0.000 0.000 0.000
.Q4_4 0.000 0.000 0.000
.Q4_5 0.000 0.000 0.000
.Q4_9 0.000 0.000 0.000
.Q4_11 0.000 0.000 0.000
.Q4_15 0.000 0.000 0.000
.Q4_18 0.000 0.000 0.000
.Q5_1 0.000 0.000 0.000
.Q5_2 0.000 0.000 0.000
.Q5_3 0.000 0.000 0.000
.Q5_5 0.000 0.000 0.000
.Q5_6 0.000 0.000 0.000
.Q5_12 0.000 0.000 0.000
.Q6_2 0.000 0.000 0.000
.Q6_5 0.000 0.000 0.000
.Q6_6 0.000 0.000 0.000
.Q6_7 0.000 0.000 0.000
.Q6_8 0.000 0.000 0.000
.Q6_11 0.000 0.000 0.000
.Q7_2 0.000 0.000 0.000
.Q7_4 0.000 0.000 0.000
.Q7_5 0.000 0.000 0.000
.Q7_7 0.000 0.000 0.000
.Q7_8 0.000 0.000 0.000
.Q7_14 0.000 0.000 0.000
EL 0.000 0.000 0.000
SC 0.000 0.000 0.000
IN 0.000 0.000 0.000
EN 0.000 0.000 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Q4_3|t1 -0.106 0.090 -1.181 0.238 -0.106 -0.067
Q4_3|t2 2.073 0.136 15.218 0.000 2.073 1.305
Q4_4|t1 -0.241 0.115 -2.098 0.036 -0.241 -0.118
Q4_4|t2 2.644 0.185 14.260 0.000 2.644 1.293
Q4_5|t1 0.317 0.090 3.516 0.000 0.317 0.206
Q4_5|t2 1.938 0.128 15.163 0.000 1.938 1.259
Q4_9|t1 0.091 0.078 1.168 0.243 0.091 0.067
Q4_9|t2 1.292 0.097 13.316 0.000 1.292 0.941
Q4_11|t1 0.017 0.093 0.180 0.857 0.017 0.010
Q4_11|t2 1.716 0.126 13.628 0.000 1.716 1.050
Q4_15|t1 0.105 0.091 1.163 0.245 0.105 0.067
Q4_15|t2 1.974 0.139 14.200 0.000 1.974 1.247
Q4_18|t1 0.258 0.109 2.368 0.018 0.258 0.139
Q4_18|t2 2.672 0.190 14.079 0.000 2.672 1.436
Q5_1|t1 -0.121 0.083 -1.451 0.147 -0.121 -0.082
Q5_1|t2 1.251 0.104 12.001 0.000 1.251 0.849
Q5_2|t1 -0.493 0.085 -5.781 0.000 -0.493 -0.339
Q5_2|t2 0.501 0.084 5.987 0.000 0.501 0.344
Q5_3|t1 -0.146 0.081 -1.813 0.070 -0.146 -0.102
Q5_3|t2 0.987 0.094 10.505 0.000 0.987 0.691
Q5_5|t1 -1.021 0.090 -11.329 0.000 -1.021 -0.771
Q5_5|t2 -0.163 0.076 -2.143 0.032 -0.163 -0.123
Q5_6|t1 -0.737 0.101 -7.317 0.000 -0.737 -0.444
Q5_6|t2 1.000 0.106 9.460 0.000 1.000 0.602
Q5_12|t1 -0.641 0.098 -6.572 0.000 -0.641 -0.394
Q5_12|t2 1.001 0.108 9.310 0.000 1.001 0.615
Q6_2|t1 0.788 0.098 8.044 0.000 0.788 0.542
Q6_2|t2 1.845 0.133 13.877 0.000 1.845 1.270
Q6_5|t1 0.128 0.068 1.886 0.059 0.128 0.108
Q6_5|t2 0.979 0.079 12.392 0.000 0.979 0.820
Q6_6|t1 1.934 0.262 7.394 0.000 1.934 0.941
Q6_6|t2 3.402 0.391 8.706 0.000 3.402 1.655
Q6_7|t1 0.701 0.126 5.564 0.000 0.701 0.372
Q6_7|t2 2.509 0.216 11.601 0.000 2.509 1.330
Q6_8|t1 0.655 0.107 6.131 0.000 0.655 0.399
Q6_8|t2 2.244 0.170 13.237 0.000 2.244 1.368
Q6_11|t1 -0.633 0.120 -5.279 0.000 -0.633 -0.323
Q6_11|t2 1.513 0.156 9.676 0.000 1.513 0.771
Q7_2|t1 -0.396 0.092 -4.325 0.000 -0.396 -0.248
Q7_2|t2 1.718 0.125 13.767 0.000 1.718 1.077
Q7_4|t1 -0.455 0.081 -5.608 0.000 -0.455 -0.323
Q7_4|t2 0.911 0.087 10.467 0.000 0.911 0.646
Q7_5|t1 -0.661 0.101 -6.551 0.000 -0.661 -0.388
Q7_5|t2 1.220 0.107 11.362 0.000 1.220 0.717
Q7_7|t1 -1.343 0.116 -11.624 0.000 -1.343 -0.909
Q7_7|t2 -0.421 0.090 -4.696 0.000 -0.421 -0.285
Q7_8|t1 -0.546 0.086 -6.388 0.000 -0.546 -0.372
Q7_8|t2 1.103 0.093 11.889 0.000 1.103 0.750
Q7_14|t1 -1.257 0.095 -13.256 0.000 -1.257 -0.965
Q7_14|t2 -0.187 0.075 -2.503 0.012 -0.187 -0.144
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
EL 1.522 0.237 6.417 0.000 1.000 1.000
SC 1.171 0.229 5.119 0.000 1.000 1.000
IN 1.111 0.234 4.753 0.000 1.000 1.000
EN 1.545 0.275 5.620 0.000 1.000 1.000
.Q4_3 1.000 1.000 0.396
.Q4_4 1.000 1.000 0.239
.Q4_5 1.000 1.000 0.422
.Q4_9 1.000 1.000 0.530
.Q4_11 1.000 1.000 0.374
.Q4_15 1.000 1.000 0.399
.Q4_18 1.000 1.000 0.289
.Q5_1 1.000 1.000 0.461
.Q5_2 1.000 1.000 0.473
.Q5_3 1.000 1.000 0.490
.Q5_5 1.000 1.000 0.570
.Q5_6 1.000 1.000 0.363
.Q5_12 1.000 1.000 0.377
.Q6_2 1.000 1.000 0.474
.Q6_5 1.000 1.000 0.702
.Q6_6 1.000 1.000 0.237
.Q6_7 1.000 1.000 0.281
.Q6_8 1.000 1.000 0.371
.Q6_11 1.000 1.000 0.260
.Q7_2 1.000 1.000 0.393
.Q7_4 1.000 1.000 0.503
.Q7_5 1.000 1.000 0.345
.Q7_7 1.000 1.000 0.458
.Q7_8 1.000 1.000 0.463
.Q7_14 1.000 1.000 0.589
Scales y*:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Q4_3 0.630 0.630 1.000
Q4_4 0.489 0.489 1.000
Q4_5 0.650 0.650 1.000
Q4_9 0.728 0.728 1.000
Q4_11 0.612 0.612 1.000
Q4_15 0.632 0.632 1.000
Q4_18 0.537 0.537 1.000
Q5_1 0.679 0.679 1.000
Q5_2 0.688 0.688 1.000
Q5_3 0.700 0.700 1.000
Q5_5 0.755 0.755 1.000
Q5_6 0.603 0.603 1.000
Q5_12 0.614 0.614 1.000
Q6_2 0.688 0.688 1.000
Q6_5 0.838 0.838 1.000
Q6_6 0.486 0.486 1.000
Q6_7 0.530 0.530 1.000
Q6_8 0.609 0.609 1.000
Q6_11 0.510 0.510 1.000
Q7_2 0.627 0.627 1.000
Q7_4 0.709 0.709 1.000
Q7_5 0.587 0.587 1.000
Q7_7 0.677 0.677 1.000
Q7_8 0.680 0.680 1.000
Q7_14 0.768 0.768 1.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
rEL 0.889 0.013 68.903 0.000 0.920 0.824
rSC 0.863 0.020 42.191 0.000 0.878 0.785
rIN 0.908 0.016 56.391 0.000 0.915 0.801
rEN 0.825 0.022 37.817 0.000 0.871 0.781Model 3: Misclassification in IFA
Model details
cat(read_file(paste0(w.d, "/code/pools_study/model_misclass_ifa.txt")))model {
### Model
for(p in 1:N){
for(i in 1:nit){
# data model
y[p,i] ~ dcat(omega[p,i, ])
# LRV
ystar[p,i] ~ dnorm(lambda[i]*ksi[p,map[nit]], 1)
# Pr(nu = 3)
pi[p,i,3] = phi(ystar[p,i] - tau[i,2])
# Pr(nu = 2)
pi[p,i,2] = phi(ystar[p,i] - tau[i,1]) - phi(ystar[p,i] - tau[i,2])
# Pr(nu = 1)
pi[p,i,1] = 1 - phi(ystar[p,i] - tau[i,1])
# compute misclassificatication based prob
# observed category prob (Pr(y=c))
for(c in 1:ncat){
omega[p,i, c] = gamma[i,c,1]*pi[p,i,1] +
gamma[i,c,2]*pi[p,i,2] +
gamma[i,c,3]*pi[p,i,3]
}
}
}
### Priors
# misclassification
for(i in 1:nit){
for(c in 1:ncat){
gamma[i,c,1:ncat] ~ ddirch(xi*alpha[c,1:ncat])
}
}
# person parameters
for(p in 1:N){
#eta[p] ~ dnorm(0, 1) # latent ability
ksi[p, 1:M] ~ dmnorm(kappa[], inv.phi[,])
}
for(m in 1:M){
kappa[m] <- 0 # Means of latent variables
}
inv.phi[1:M,1:M] ~ dwish(dxphi.0[ , ], d); # prior for precision matrix for the latent variables
phi[1:M,1:M] <- inverse(inv.phi[ , ]); # the covariance matrix for the latent vars
for(m in 1:M){
for(mm in 1:M){
dxphi.0[m,mm] <- d*phi.0[m,mm];
}
}
# factor correlations
for(m in 1:M){
for(mm in 1:M){
phi.cor[m,mm] = (phi[m,mm])/((pow(phi[m,m], 0.5))*(pow(phi[mm,mm], 0.5)));
}
}
# priors for loadings
# loadings
lambda[1] = 1
lambda[8] = 1
lambda[13] = 1
lambda[19] = 1
for(i in 2:7){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 9:12){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 14:18){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 20:25){
lambda[i] ~ dnorm(0, 1)T(0,)
}
for(i in 1:nit){
# Thresholds
tau[i, 1] = 0
tau[i, 2] ~ dnorm(0, 0.1)T(tau[i, 1],)
# LRV total variance
# total variance = residual variance + fact. Var.
theta[i] = 1 + pow(lambda[i],2)
# standardized loading
lambda.std[i] = lambda[i]/pow(theta[i],0.5)
}
# compute omega
lambda_sum1[1] = lambda[1]
lambda_sum2[1] = lambda[8]
lambda_sum3[1] = lambda[13]
lambda_sum4[1] = lambda[19]
for(i in 2:6){
#lambda_sum (sum factor loadings)
lambda_sum1[i] = lambda_sum1[i-1]+lambda[i]
lambda_sum2[i] = lambda_sum2[i-1]+lambda[i+7]
lambda_sum3[i] = lambda_sum3[i-1]+lambda[i+12]
lambda_sum4[i] = lambda_sum4[i-1]+lambda[i+18]
}
lambda_sum1[7] = lambda_sum1[6] + lambda[7]
# compute reliability
reli.omega[1] = (pow(lambda_sum1[7],2))/(pow(lambda_sum1[7],2)+7)
reli.omega[2] = (pow(lambda_sum2[6],2))/(pow(lambda_sum2[6],2)+6)
reli.omega[3] = (pow(lambda_sum3[6],2))/(pow(lambda_sum3[6],2)+6)
reli.omega[4] = (pow(lambda_sum4[6],2))/(pow(lambda_sum4[6],2)+6)
}Model results
# Save parameters
jags.params <- c("tau", "lambda", "theta", "reli.omega", "lambda.std",
"phi.cor", "inv.phi", "phi", "gamma")
# initial-values
jags.inits <- function(){
list(
"inv.phi"=solve(matrix(
c(1.52, 0.92, 0.97, 1.19,
0.92, 1.17, 0.74, 1.08,
0.97, 0.74, 1.11, 0.98,
1.19, 1.08, 0.98, 1.55), ncol=4, nrow=4, byrow=T
))
)
}
# data
jags.data <- list(
y = mydata,
N = nrow(mydata),
nit = ncol(mydata),
map = c(rep(1,7), rep(2,6), rep(3,6), rep(4,6)),
d = 8,
M = 4,
phi.0 = matrix(
c(1, 0.69, 0.75, 0.78,
0.69, 1, 0.65, 0.80,
0.75, 0.65, 1, 0.75,
0.78, 0.80, 0.75, 1), ncol=4, nrow=4, byrow=T
),
ncat = 3,
alpha = matrix(
c(0.85, 0.10, 0.05,
0, 0.90, 0.10,
0.0, 0, 1),
ncol=3, nrow=3, byrow=T
),
xi = 10
)
model.fit <- R2jags::jags(
model = paste0(w.d, "/code/pools_study/model_misclass_ifa.txt"),
parameters.to.save = jags.params,
inits = jags.inits,
data = jags.data,
n.chains = 4,
n.burnin = 5000,
n.iter = 10000
)module glm loadedCompiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 12250
Unobserved stochastic nodes: 12862
Total graph size: 269608
Initializing modelprint(model.fit, width=1000)Inference for Bugs model at "C:/Users/noahp/Documents/GitHub/Padgett-Dissertation/code/pools_study/model_misclass_ifa.txt", fit using jags,
4 chains, each with 10000 iterations (first 5000 discarded), n.thin = 5
n.sims = 4000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
gamma[1,1,1] 0.787 0.069 0.641 0.743 0.789 0.836 0.913 1.00 4000
gamma[2,1,1] 0.830 0.058 0.703 0.793 0.835 0.871 0.932 1.01 390
gamma[3,1,1] 0.619 0.092 0.436 0.554 0.623 0.685 0.789 1.01 410
gamma[4,1,1] 0.588 0.097 0.399 0.522 0.588 0.654 0.781 1.01 300
gamma[5,1,1] 0.762 0.080 0.597 0.710 0.768 0.818 0.914 1.00 780
gamma[6,1,1] 0.757 0.085 0.579 0.702 0.760 0.817 0.911 1.00 910
gamma[7,1,1] 0.798 0.070 0.649 0.754 0.800 0.848 0.925 1.01 470
gamma[8,1,1] 0.764 0.090 0.572 0.706 0.773 0.828 0.924 1.00 1400
gamma[9,1,1] 0.862 0.116 0.567 0.815 0.895 0.947 0.991 1.01 370
gamma[10,1,1] 0.777 0.112 0.524 0.703 0.789 0.860 0.956 1.00 1000
gamma[11,1,1] 0.233 0.061 0.122 0.189 0.230 0.273 0.360 1.00 1200
gamma[12,1,1] 0.956 0.033 0.872 0.940 0.965 0.981 0.997 1.00 1500
gamma[13,1,1] 0.962 0.030 0.887 0.948 0.971 0.985 0.997 1.00 3200
gamma[14,1,1] 0.628 0.125 0.383 0.544 0.625 0.716 0.872 1.00 790
gamma[15,1,1] 0.820 0.111 0.584 0.747 0.836 0.911 0.984 1.01 300
gamma[16,1,1] 0.630 0.114 0.387 0.555 0.633 0.710 0.841 1.01 340
gamma[17,1,1] 0.698 0.103 0.480 0.630 0.702 0.772 0.887 1.01 250
gamma[18,1,1] 0.751 0.105 0.529 0.682 0.758 0.827 0.938 1.01 230
gamma[19,1,1] 0.952 0.034 0.867 0.935 0.960 0.977 0.995 1.00 1300
gamma[20,1,1] 0.867 0.060 0.731 0.830 0.874 0.913 0.962 1.01 450
gamma[21,1,1] 0.880 0.064 0.740 0.839 0.888 0.927 0.980 1.00 700
gamma[22,1,1] 0.971 0.023 0.912 0.960 0.977 0.988 0.998 1.01 760
gamma[23,1,1] 0.105 0.039 0.040 0.076 0.101 0.129 0.190 1.00 4000
gamma[24,1,1] 0.956 0.035 0.869 0.937 0.964 0.982 0.997 1.01 560
gamma[25,1,1] 0.133 0.037 0.068 0.107 0.130 0.156 0.213 1.01 460
gamma[1,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[2,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[3,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[4,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[5,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[6,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[7,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[8,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[9,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[10,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[11,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[12,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[13,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[14,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[15,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[16,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[17,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[18,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[19,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[20,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[21,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[22,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[23,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[24,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[25,2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[1,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[2,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[3,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[4,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[5,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[6,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[7,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[8,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[9,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[10,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[11,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[12,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[13,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[14,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[15,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[16,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[17,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[18,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[19,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[20,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[21,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[22,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[23,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[24,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[25,3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[1,1,2] 0.191 0.067 0.066 0.143 0.188 0.235 0.333 1.01 1100
gamma[2,1,2] 0.147 0.054 0.052 0.108 0.144 0.181 0.268 1.00 4000
gamma[3,1,2] 0.346 0.091 0.178 0.280 0.339 0.409 0.536 1.01 280
gamma[4,1,2] 0.337 0.108 0.124 0.262 0.340 0.412 0.540 1.00 750
gamma[5,1,2] 0.218 0.081 0.062 0.163 0.214 0.271 0.381 1.01 1800
gamma[6,1,2] 0.226 0.086 0.071 0.163 0.224 0.282 0.404 1.01 430
gamma[7,1,2] 0.173 0.067 0.053 0.125 0.170 0.214 0.315 1.08 88
gamma[8,1,2] 0.190 0.099 0.012 0.119 0.185 0.254 0.393 1.11 91
gamma[9,1,2] 0.123 0.114 0.003 0.038 0.089 0.172 0.412 1.02 350
gamma[10,1,2] 0.159 0.113 0.007 0.070 0.136 0.230 0.428 1.02 270
gamma[11,1,2] 0.751 0.060 0.628 0.713 0.753 0.792 0.864 1.00 4000
gamma[12,1,2] 0.026 0.026 0.001 0.008 0.018 0.036 0.099 1.01 450
gamma[13,1,2] 0.026 0.026 0.001 0.008 0.019 0.037 0.097 1.00 3100
gamma[14,1,2] 0.346 0.125 0.096 0.259 0.346 0.434 0.591 1.00 610
gamma[15,1,2] 0.135 0.104 0.003 0.047 0.113 0.200 0.377 1.01 400
gamma[16,1,2] 0.346 0.111 0.150 0.267 0.342 0.418 0.582 1.00 830
gamma[17,1,2] 0.263 0.100 0.087 0.194 0.258 0.330 0.475 1.01 330
gamma[18,1,2] 0.229 0.104 0.046 0.154 0.218 0.295 0.451 1.03 140
gamma[19,1,2] 0.029 0.027 0.001 0.009 0.020 0.040 0.100 1.01 590
gamma[20,1,2] 0.057 0.041 0.003 0.024 0.050 0.082 0.156 1.01 550
gamma[21,1,2] 0.053 0.048 0.002 0.018 0.040 0.072 0.175 1.01 4000
gamma[22,1,2] 0.019 0.019 0.000 0.006 0.014 0.027 0.070 1.00 2300
gamma[23,1,2] 0.890 0.039 0.805 0.865 0.894 0.919 0.955 1.00 1900
gamma[24,1,2] 0.025 0.024 0.001 0.008 0.019 0.035 0.087 1.00 1100
gamma[25,1,2] 0.861 0.037 0.781 0.838 0.864 0.887 0.926 1.00 560
gamma[1,2,2] 0.905 0.078 0.711 0.862 0.926 0.966 0.997 1.00 1400
gamma[2,2,2] 0.883 0.079 0.700 0.836 0.896 0.943 0.993 1.00 2300
gamma[3,2,2] 0.565 0.105 0.371 0.491 0.560 0.630 0.781 1.00 740
gamma[4,2,2] 0.837 0.110 0.582 0.766 0.854 0.925 0.991 1.00 540
gamma[5,2,2] 0.813 0.110 0.572 0.737 0.819 0.899 0.988 1.00 1700
gamma[6,2,2] 0.726 0.123 0.500 0.635 0.725 0.821 0.958 1.01 460
gamma[7,2,2] 0.508 0.113 0.297 0.427 0.503 0.583 0.744 1.02 140
gamma[8,2,2] 0.847 0.093 0.638 0.787 0.857 0.920 0.988 1.00 1000
gamma[9,2,2] 0.786 0.099 0.572 0.725 0.795 0.856 0.958 1.00 3400
gamma[10,2,2] 0.938 0.054 0.808 0.912 0.952 0.979 0.998 1.00 740
gamma[11,2,2] 0.622 0.053 0.518 0.586 0.621 0.658 0.727 1.00 3100
gamma[12,2,2] 0.952 0.038 0.853 0.931 0.961 0.982 0.998 1.00 4000
gamma[13,2,2] 0.948 0.042 0.842 0.926 0.958 0.981 0.998 1.00 4000
gamma[14,2,2] 0.210 0.047 0.128 0.176 0.208 0.240 0.309 1.00 1200
gamma[15,2,2] 0.597 0.153 0.316 0.487 0.588 0.701 0.907 1.00 770
gamma[16,2,2] 0.092 0.025 0.050 0.074 0.090 0.108 0.150 1.00 1300
gamma[17,2,2] 0.295 0.069 0.175 0.245 0.292 0.339 0.445 1.00 590
gamma[18,2,2] 0.285 0.065 0.172 0.238 0.279 0.328 0.425 1.01 290
gamma[19,2,2] 0.970 0.029 0.890 0.958 0.979 0.991 0.999 1.00 1100
gamma[20,2,2] 0.934 0.053 0.802 0.906 0.946 0.975 0.998 1.02 220
gamma[21,2,2] 0.953 0.042 0.840 0.936 0.965 0.985 0.998 1.00 4000
gamma[22,2,2] 0.942 0.045 0.830 0.919 0.951 0.977 0.997 1.00 1100
gamma[23,2,2] 0.750 0.063 0.634 0.705 0.749 0.794 0.876 1.00 2300
gamma[24,2,2] 0.944 0.050 0.811 0.920 0.958 0.982 0.998 1.00 4000
gamma[25,2,2] 0.541 0.053 0.439 0.504 0.542 0.576 0.644 1.00 2200
gamma[1,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[2,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[3,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[4,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[5,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[6,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[7,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[8,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[9,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[10,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[11,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[12,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[13,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[14,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[15,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[16,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[17,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[18,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[19,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[20,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[21,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[22,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[23,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[24,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[25,3,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
gamma[1,1,3] 0.021 0.031 0.000 0.002 0.009 0.028 0.111 1.01 330
gamma[2,1,3] 0.023 0.029 0.000 0.004 0.013 0.032 0.102 1.03 170
gamma[3,1,3] 0.035 0.046 0.000 0.004 0.017 0.047 0.169 1.02 280
gamma[4,1,3] 0.075 0.063 0.001 0.023 0.060 0.114 0.229 1.03 140
gamma[5,1,3] 0.020 0.029 0.000 0.002 0.008 0.025 0.103 1.09 56
gamma[6,1,3] 0.018 0.023 0.000 0.002 0.010 0.025 0.081 1.01 200
gamma[7,1,3] 0.029 0.035 0.000 0.005 0.017 0.040 0.128 1.06 57
gamma[8,1,3] 0.046 0.051 0.000 0.007 0.029 0.068 0.185 1.11 45
gamma[9,1,3] 0.015 0.020 0.000 0.002 0.007 0.022 0.067 1.01 460
gamma[10,1,3] 0.065 0.060 0.000 0.015 0.049 0.098 0.217 1.02 170
gamma[11,1,3] 0.016 0.017 0.000 0.002 0.010 0.024 0.062 1.05 110
gamma[12,1,3] 0.017 0.022 0.000 0.002 0.009 0.024 0.081 1.00 1300
gamma[13,1,3] 0.011 0.015 0.000 0.001 0.005 0.015 0.054 1.03 150
gamma[14,1,3] 0.026 0.033 0.000 0.003 0.013 0.035 0.119 1.02 240
gamma[15,1,3] 0.045 0.055 0.000 0.007 0.024 0.063 0.211 1.01 390
gamma[16,1,3] 0.024 0.031 0.000 0.004 0.012 0.032 0.117 1.03 110
gamma[17,1,3] 0.038 0.044 0.000 0.006 0.021 0.055 0.157 1.03 180
gamma[18,1,3] 0.021 0.030 0.000 0.001 0.008 0.028 0.105 1.11 63
gamma[19,1,3] 0.019 0.022 0.000 0.003 0.011 0.027 0.082 1.03 150
gamma[20,1,3] 0.076 0.060 0.001 0.028 0.063 0.112 0.214 1.01 540
gamma[21,1,3] 0.067 0.052 0.001 0.027 0.058 0.098 0.188 1.02 520
gamma[22,1,3] 0.010 0.014 0.000 0.001 0.004 0.013 0.050 1.12 63
gamma[23,1,3] 0.004 0.006 0.000 0.001 0.002 0.006 0.021 1.06 340
gamma[24,1,3] 0.019 0.026 0.000 0.002 0.009 0.026 0.097 1.01 280
gamma[25,1,3] 0.006 0.008 0.000 0.001 0.003 0.008 0.029 1.02 250
gamma[1,2,3] 0.095 0.078 0.003 0.034 0.074 0.138 0.289 1.00 1600
gamma[2,2,3] 0.117 0.079 0.007 0.057 0.104 0.164 0.300 1.00 4000
gamma[3,2,3] 0.435 0.105 0.219 0.370 0.440 0.509 0.629 1.01 750
gamma[4,2,3] 0.163 0.110 0.009 0.075 0.146 0.234 0.418 1.01 550
gamma[5,2,3] 0.187 0.110 0.012 0.101 0.181 0.263 0.428 1.00 970
gamma[6,2,3] 0.274 0.123 0.042 0.179 0.275 0.365 0.500 1.01 430
gamma[7,2,3] 0.492 0.113 0.256 0.417 0.497 0.573 0.703 1.01 220
gamma[8,2,3] 0.153 0.093 0.012 0.080 0.143 0.213 0.362 1.00 1100
gamma[9,2,3] 0.214 0.099 0.042 0.144 0.205 0.275 0.428 1.01 1200
gamma[10,2,3] 0.062 0.054 0.002 0.021 0.048 0.088 0.192 1.00 830
gamma[11,2,3] 0.378 0.053 0.273 0.342 0.379 0.414 0.482 1.00 3300
gamma[12,2,3] 0.048 0.038 0.002 0.018 0.039 0.069 0.147 1.00 910
gamma[13,2,3] 0.052 0.042 0.002 0.019 0.042 0.074 0.158 1.00 4000
gamma[14,2,3] 0.790 0.047 0.691 0.760 0.792 0.824 0.872 1.00 1100
gamma[15,2,3] 0.403 0.153 0.093 0.299 0.412 0.513 0.684 1.01 770
gamma[16,2,3] 0.908 0.025 0.850 0.892 0.910 0.926 0.950 1.00 1500
gamma[17,2,3] 0.705 0.069 0.555 0.661 0.708 0.755 0.825 1.00 640
gamma[18,2,3] 0.715 0.065 0.575 0.672 0.721 0.762 0.828 1.01 310
gamma[19,2,3] 0.030 0.029 0.001 0.009 0.021 0.042 0.110 1.00 940
gamma[20,2,3] 0.066 0.053 0.002 0.025 0.054 0.094 0.198 1.01 390
gamma[21,2,3] 0.047 0.042 0.002 0.015 0.035 0.064 0.160 1.00 2700
gamma[22,2,3] 0.058 0.045 0.003 0.023 0.049 0.081 0.170 1.01 370
gamma[23,2,3] 0.250 0.063 0.124 0.206 0.251 0.295 0.366 1.00 4000
gamma[24,2,3] 0.056 0.050 0.002 0.018 0.042 0.080 0.189 1.00 2800
gamma[25,2,3] 0.459 0.053 0.356 0.424 0.458 0.496 0.561 1.00 1900
gamma[1,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[2,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[3,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[4,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[5,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[6,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[7,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[8,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[9,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[10,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[11,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[12,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[13,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[14,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[15,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[16,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[17,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[18,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[19,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[20,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[21,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[22,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[23,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[24,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
gamma[25,3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
inv.phi[1,1] 3.199 1.546 0.898 2.039 2.957 4.082 6.881 1.03 110
inv.phi[2,1] -0.518 1.063 -2.782 -1.166 -0.502 0.173 1.566 1.05 53
inv.phi[3,1] -1.166 1.121 -3.742 -1.794 -1.040 -0.415 0.718 1.06 54
inv.phi[4,1] -1.191 1.351 -4.239 -1.975 -1.037 -0.236 0.988 1.04 68
inv.phi[1,2] -0.518 1.063 -2.782 -1.166 -0.502 0.173 1.566 1.05 53
inv.phi[2,2] 2.927 1.511 0.675 1.831 2.641 3.788 6.543 1.10 34
inv.phi[3,2] -0.100 0.945 -2.180 -0.634 -0.064 0.502 1.649 1.03 82
inv.phi[4,2] -1.998 1.420 -5.256 -2.807 -1.752 -0.934 0.068 1.05 62
inv.phi[1,3] -1.166 1.121 -3.742 -1.794 -1.040 -0.415 0.718 1.06 54
inv.phi[2,3] -0.100 0.945 -2.180 -0.634 -0.064 0.502 1.649 1.03 82
inv.phi[3,3] 2.600 1.321 0.705 1.600 2.389 3.316 5.707 1.05 59
inv.phi[4,3] -0.823 1.267 -3.622 -1.597 -0.689 0.099 1.335 1.05 65
inv.phi[1,4] -1.191 1.351 -4.239 -1.975 -1.037 -0.236 0.988 1.04 68
inv.phi[2,4] -1.998 1.420 -5.256 -2.807 -1.752 -0.934 0.068 1.05 62
inv.phi[3,4] -0.823 1.267 -3.622 -1.597 -0.689 0.099 1.335 1.05 65
inv.phi[4,4] 3.886 2.180 0.770 2.237 3.498 5.155 9.043 1.03 95
lambda[1] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[2] 1.459 0.182 1.127 1.330 1.447 1.579 1.842 1.01 620
lambda[3] 1.359 0.178 1.047 1.234 1.344 1.471 1.735 1.01 460
lambda[4] 1.014 0.130 0.764 0.928 1.008 1.097 1.291 1.02 100
lambda[5] 1.127 0.125 0.904 1.040 1.122 1.212 1.384 1.01 500
lambda[6] 1.086 0.135 0.835 0.993 1.084 1.176 1.361 1.01 240
lambda[7] 1.415 0.184 1.098 1.281 1.401 1.537 1.796 1.01 330
lambda[8] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[9] 0.864 0.094 0.688 0.799 0.861 0.926 1.052 1.02 140
lambda[10] 0.756 0.095 0.585 0.690 0.749 0.817 0.962 1.01 230
lambda[11] 0.763 0.101 0.578 0.692 0.758 0.828 0.974 1.01 290
lambda[12] 0.923 0.088 0.767 0.861 0.920 0.980 1.108 1.01 290
lambda[13] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[14] 0.827 0.130 0.576 0.740 0.823 0.915 1.086 1.02 110
lambda[15] 0.490 0.074 0.358 0.439 0.485 0.537 0.646 1.02 180
lambda[16] 1.398 0.247 0.963 1.227 1.384 1.559 1.917 1.02 120
lambda[17] 1.295 0.209 0.927 1.136 1.281 1.452 1.697 1.04 71
lambda[18] 0.907 0.139 0.657 0.811 0.900 0.993 1.206 1.02 160
lambda[19] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
lambda[20] 1.197 0.129 0.969 1.107 1.190 1.282 1.472 1.01 760
lambda[21] 0.957 0.102 0.769 0.884 0.952 1.024 1.165 1.00 870
lambda[22] 1.111 0.101 0.925 1.041 1.108 1.175 1.319 1.01 240
lambda[23] 0.935 0.112 0.731 0.857 0.928 1.005 1.179 1.01 270
lambda[24] 0.911 0.090 0.754 0.847 0.903 0.965 1.109 1.01 430
lambda[25] 0.840 0.101 0.655 0.770 0.836 0.904 1.055 1.01 250
lambda.std[1] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[2] 0.821 0.033 0.748 0.799 0.823 0.845 0.879 1.01 840
lambda.std[3] 0.801 0.037 0.723 0.777 0.802 0.827 0.866 1.01 390
lambda.std[4] 0.708 0.045 0.607 0.680 0.710 0.739 0.791 1.02 110
lambda.std[5] 0.745 0.037 0.671 0.721 0.747 0.771 0.810 1.01 420
lambda.std[6] 0.731 0.042 0.641 0.705 0.735 0.762 0.806 1.01 270
lambda.std[7] 0.812 0.036 0.739 0.788 0.814 0.838 0.874 1.01 290
lambda.std[8] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[9] 0.651 0.041 0.567 0.624 0.652 0.680 0.725 1.02 140
lambda.std[10] 0.600 0.048 0.505 0.568 0.599 0.633 0.693 1.02 210
lambda.std[11] 0.603 0.050 0.500 0.569 0.604 0.638 0.698 1.01 290
lambda.std[12] 0.676 0.035 0.609 0.652 0.677 0.700 0.742 1.01 290
lambda.std[13] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[14] 0.632 0.060 0.499 0.595 0.635 0.675 0.736 1.03 110
lambda.std[15] 0.438 0.053 0.337 0.402 0.436 0.473 0.542 1.02 180
lambda.std[16] 0.805 0.050 0.694 0.775 0.811 0.842 0.887 1.02 140
lambda.std[17] 0.784 0.049 0.680 0.751 0.788 0.824 0.862 1.04 79
lambda.std[18] 0.666 0.056 0.549 0.630 0.669 0.705 0.770 1.03 140
lambda.std[19] 0.707 0.000 0.707 0.707 0.707 0.707 0.707 1.00 1
lambda.std[20] 0.764 0.034 0.696 0.742 0.765 0.789 0.827 1.01 820
lambda.std[21] 0.688 0.038 0.610 0.662 0.690 0.715 0.759 1.00 830
lambda.std[22] 0.741 0.030 0.679 0.721 0.742 0.762 0.797 1.01 220
lambda.std[23] 0.679 0.043 0.590 0.651 0.680 0.709 0.763 1.01 270
lambda.std[24] 0.671 0.036 0.602 0.646 0.670 0.694 0.743 1.01 420
lambda.std[25] 0.640 0.045 0.548 0.610 0.641 0.671 0.726 1.01 240
phi[1,1] 2.590 1.414 0.715 1.511 2.328 3.377 6.130 1.01 580
phi[2,1] 2.025 1.217 0.210 1.174 1.873 2.761 4.778 1.04 110
phi[3,1] 1.865 1.277 0.004 1.029 1.679 2.467 4.959 1.03 210
phi[4,1] 2.155 0.963 0.249 1.511 2.171 2.824 4.002 1.01 400
phi[1,2] 2.025 1.217 0.210 1.174 1.873 2.761 4.778 1.04 110
phi[2,2] 3.217 2.517 0.965 1.891 2.635 3.774 9.479 1.13 32
phi[3,2] 1.776 1.279 -0.596 1.029 1.731 2.471 4.346 1.04 180
phi[4,2] 2.525 0.954 0.730 1.921 2.469 3.092 4.438 1.09 46
phi[1,3] 1.865 1.277 0.004 1.029 1.679 2.467 4.959 1.03 210
phi[2,3] 1.776 1.279 -0.596 1.029 1.731 2.471 4.346 1.04 180
phi[3,3] 2.586 1.680 0.702 1.541 2.233 3.137 6.440 1.04 120
phi[4,3] 1.914 1.134 -0.748 1.340 2.061 2.620 3.852 1.03 370
phi[1,4] 2.155 0.963 0.249 1.511 2.171 2.824 4.002 1.01 400
phi[2,4] 2.525 0.954 0.730 1.921 2.469 3.092 4.438 1.09 46
phi[3,4] 1.914 1.134 -0.748 1.340 2.061 2.620 3.852 1.03 370
phi[4,4] 2.958 0.307 2.408 2.740 2.942 3.166 3.592 1.01 220
phi.cor[1,1] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[2,1] 0.732 0.223 0.133 0.656 0.804 0.883 0.951 1.07 100
phi.cor[3,1] 0.721 0.241 0.003 0.646 0.793 0.884 0.955 1.02 170
phi.cor[4,1] 0.779 0.214 0.121 0.735 0.855 0.912 0.960 1.07 120
phi.cor[1,2] 0.732 0.223 0.133 0.656 0.804 0.883 0.951 1.07 100
phi.cor[2,2] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[3,2] 0.651 0.299 -0.245 0.566 0.757 0.848 0.930 1.05 170
phi.cor[4,2] 0.843 0.153 0.397 0.816 0.893 0.933 0.968 1.04 160
phi.cor[1,3] 0.721 0.241 0.003 0.646 0.793 0.884 0.955 1.02 170
phi.cor[2,3] 0.651 0.299 -0.245 0.566 0.757 0.848 0.930 1.05 170
phi.cor[3,3] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
phi.cor[4,3] 0.698 0.321 -0.348 0.655 0.818 0.892 0.947 1.06 97
phi.cor[1,4] 0.779 0.214 0.121 0.735 0.855 0.912 0.960 1.07 120
phi.cor[2,4] 0.843 0.153 0.397 0.816 0.893 0.933 0.968 1.04 160
phi.cor[3,4] 0.698 0.321 -0.348 0.655 0.818 0.892 0.947 1.06 97
phi.cor[4,4] 1.000 0.000 1.000 1.000 1.000 1.000 1.000 1.00 1
reli.omega[1] 0.910 0.009 0.891 0.904 0.911 0.917 0.927 1.01 660
reli.omega[2] 0.824 0.012 0.799 0.815 0.824 0.833 0.846 1.03 95
reli.omega[3] 0.852 0.020 0.812 0.838 0.853 0.866 0.888 1.02 230
reli.omega[4] 0.861 0.012 0.837 0.853 0.861 0.869 0.884 1.02 190
tau[1,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[4,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[5,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[6,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[7,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[8,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[9,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[10,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[11,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[12,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[13,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[14,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[15,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[16,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[17,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[18,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[19,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[20,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[21,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[22,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[23,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[24,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[25,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.00 1
tau[1,2] 3.126 0.166 2.802 3.013 3.125 3.242 3.455 1.00 890
tau[2,2] 4.009 0.364 3.375 3.754 3.987 4.244 4.812 1.01 230
tau[3,2] 3.623 0.317 3.038 3.399 3.610 3.831 4.283 1.00 2500
tau[4,2] 2.206 0.181 1.865 2.085 2.204 2.316 2.583 1.02 150
tau[5,2] 2.736 0.210 2.348 2.591 2.726 2.871 3.163 1.01 540
tau[6,2] 3.155 0.253 2.685 2.981 3.145 3.317 3.694 1.01 420
tau[7,2] 4.327 0.388 3.642 4.053 4.297 4.565 5.171 1.01 240
tau[8,2] 2.049 0.130 1.796 1.961 2.049 2.137 2.308 1.00 1300
tau[9,2] 0.955 0.141 0.656 0.869 0.965 1.054 1.198 1.00 4000
tau[10,2] 1.510 0.115 1.289 1.430 1.508 1.587 1.744 1.00 890
tau[11,2] 0.079 0.062 0.003 0.029 0.065 0.119 0.226 1.00 4000
tau[12,2] 1.746 0.110 1.534 1.671 1.744 1.819 1.966 1.00 680
tau[13,2] 1.813 0.104 1.611 1.741 1.814 1.883 2.014 1.00 4000
tau[14,2] 2.922 0.222 2.520 2.762 2.918 3.069 3.380 1.01 230
tau[15,2] 1.424 0.137 1.167 1.330 1.423 1.516 1.701 1.00 1100
tau[16,2] 4.979 0.535 4.054 4.596 4.942 5.324 6.106 1.03 100
tau[17,2] 3.798 0.341 3.181 3.554 3.783 4.024 4.520 1.04 81
tau[18,2] 3.220 0.253 2.742 3.047 3.207 3.382 3.733 1.01 340
tau[19,2] 2.147 0.115 1.926 2.069 2.146 2.227 2.371 1.00 1600
tau[20,2] 2.988 0.208 2.608 2.844 2.972 3.119 3.424 1.00 560
tau[21,2] 1.770 0.122 1.537 1.687 1.768 1.853 2.014 1.00 2200
tau[22,2] 2.152 0.137 1.904 2.057 2.147 2.243 2.431 1.00 1000
tau[23,2] 0.138 0.079 0.009 0.074 0.135 0.193 0.299 1.00 4000
tau[24,2] 1.979 0.124 1.748 1.893 1.976 2.060 2.232 1.00 2100
tau[25,2] 0.046 0.040 0.001 0.016 0.035 0.066 0.145 1.00 1100
theta[1] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[2] 3.161 0.542 2.269 2.770 3.094 3.492 4.392 1.01 540
theta[3] 2.878 0.496 2.096 2.523 2.807 3.164 4.009 1.00 510
theta[4] 2.045 0.269 1.584 1.860 2.017 2.203 2.666 1.03 100
theta[5] 2.287 0.286 1.818 2.081 2.259 2.468 2.915 1.01 570
theta[6] 2.198 0.298 1.697 1.986 2.175 2.383 2.851 1.01 220
theta[7] 3.035 0.534 2.206 2.641 2.963 3.364 4.227 1.01 350
theta[8] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[9] 1.756 0.166 1.473 1.638 1.741 1.858 2.107 1.02 140
theta[10] 1.581 0.148 1.342 1.476 1.561 1.667 1.926 1.01 270
theta[11] 1.592 0.158 1.334 1.479 1.574 1.686 1.949 1.01 290
theta[12] 1.860 0.164 1.588 1.741 1.846 1.961 2.227 1.01 280
theta[13] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[14] 1.702 0.219 1.332 1.547 1.677 1.838 2.179 1.02 120
theta[15] 1.246 0.075 1.128 1.192 1.235 1.289 1.417 1.02 180
theta[16] 3.016 0.714 1.928 2.504 2.915 3.431 4.677 1.03 110
theta[17] 2.720 0.553 1.860 2.291 2.640 3.109 3.881 1.04 68
theta[18] 1.842 0.263 1.432 1.657 1.810 1.987 2.455 1.02 200
theta[19] 2.000 0.000 2.000 2.000 2.000 2.000 2.000 1.00 1
theta[20] 2.451 0.314 1.939 2.226 2.415 2.644 3.168 1.01 710
theta[21] 1.926 0.197 1.591 1.781 1.907 2.049 2.357 1.00 920
theta[22] 2.244 0.228 1.855 2.083 2.228 2.381 2.740 1.01 250
theta[23] 1.886 0.214 1.534 1.735 1.861 2.011 2.390 1.01 270
theta[24] 1.837 0.169 1.568 1.718 1.816 1.931 2.231 1.01 450
theta[25] 1.716 0.174 1.430 1.594 1.699 1.818 2.113 1.01 280
deviance 15491.432 122.187 15248.149 15413.528 15490.959 15574.984 15725.502 1.00 780
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 7441.5 and DIC = 22932.9
DIC is an estimate of expected predictive error (lower deviance is better).kable(model.fit$BUGSoutput$summary, format="html", digits=3) %>%
kable_styling(full_width = T) %>%
scroll_box(width="100%", height="500px")| mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | Rhat | n.eff | |
|---|---|---|---|---|---|---|---|---|---|
| deviance | 15491.432 | 122.187 | 15248.149 | 15413.528 | 15490.959 | 15574.984 | 15725.502 | 1.00 | 780 |
| gamma[1,1,1] | 0.787 | 0.069 | 0.641 | 0.743 | 0.789 | 0.836 | 0.913 | 1.00 | 4000 |
| gamma[2,1,1] | 0.830 | 0.058 | 0.703 | 0.793 | 0.835 | 0.871 | 0.932 | 1.01 | 390 |
| gamma[3,1,1] | 0.619 | 0.092 | 0.436 | 0.554 | 0.623 | 0.685 | 0.789 | 1.01 | 410 |
| gamma[4,1,1] | 0.588 | 0.097 | 0.399 | 0.522 | 0.588 | 0.654 | 0.781 | 1.01 | 300 |
| gamma[5,1,1] | 0.762 | 0.080 | 0.597 | 0.710 | 0.768 | 0.818 | 0.914 | 1.00 | 780 |
| gamma[6,1,1] | 0.757 | 0.085 | 0.579 | 0.702 | 0.760 | 0.817 | 0.911 | 1.00 | 910 |
| gamma[7,1,1] | 0.798 | 0.070 | 0.649 | 0.754 | 0.800 | 0.848 | 0.925 | 1.01 | 470 |
| gamma[8,1,1] | 0.764 | 0.090 | 0.572 | 0.706 | 0.773 | 0.828 | 0.924 | 1.00 | 1400 |
| gamma[9,1,1] | 0.862 | 0.116 | 0.567 | 0.815 | 0.895 | 0.947 | 0.991 | 1.01 | 370 |
| gamma[10,1,1] | 0.777 | 0.112 | 0.524 | 0.703 | 0.789 | 0.860 | 0.956 | 1.00 | 1000 |
| gamma[11,1,1] | 0.233 | 0.061 | 0.122 | 0.189 | 0.230 | 0.273 | 0.360 | 1.00 | 1200 |
| gamma[12,1,1] | 0.956 | 0.033 | 0.872 | 0.940 | 0.965 | 0.981 | 0.997 | 1.00 | 1500 |
| gamma[13,1,1] | 0.962 | 0.030 | 0.887 | 0.948 | 0.971 | 0.985 | 0.997 | 1.00 | 3200 |
| gamma[14,1,1] | 0.628 | 0.125 | 0.383 | 0.544 | 0.625 | 0.716 | 0.872 | 1.00 | 790 |
| gamma[15,1,1] | 0.820 | 0.111 | 0.584 | 0.747 | 0.836 | 0.911 | 0.984 | 1.01 | 300 |
| gamma[16,1,1] | 0.630 | 0.114 | 0.387 | 0.555 | 0.633 | 0.710 | 0.841 | 1.01 | 340 |
| gamma[17,1,1] | 0.698 | 0.103 | 0.480 | 0.630 | 0.702 | 0.772 | 0.887 | 1.01 | 250 |
| gamma[18,1,1] | 0.751 | 0.105 | 0.529 | 0.682 | 0.758 | 0.827 | 0.938 | 1.01 | 230 |
| gamma[19,1,1] | 0.952 | 0.034 | 0.867 | 0.935 | 0.960 | 0.977 | 0.995 | 1.00 | 1300 |
| gamma[20,1,1] | 0.867 | 0.060 | 0.731 | 0.830 | 0.874 | 0.913 | 0.962 | 1.01 | 450 |
| gamma[21,1,1] | 0.880 | 0.064 | 0.740 | 0.839 | 0.888 | 0.927 | 0.980 | 1.00 | 700 |
| gamma[22,1,1] | 0.971 | 0.023 | 0.912 | 0.960 | 0.977 | 0.988 | 0.998 | 1.01 | 760 |
| gamma[23,1,1] | 0.105 | 0.039 | 0.040 | 0.076 | 0.101 | 0.129 | 0.190 | 1.00 | 4000 |
| gamma[24,1,1] | 0.956 | 0.035 | 0.869 | 0.937 | 0.964 | 0.982 | 0.997 | 1.01 | 560 |
| gamma[25,1,1] | 0.133 | 0.037 | 0.068 | 0.107 | 0.130 | 0.156 | 0.213 | 1.01 | 460 |
| gamma[1,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[2,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[3,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[4,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[5,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[6,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[7,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[8,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[9,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[10,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[11,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[12,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[13,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[14,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[15,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[16,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[17,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[18,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[19,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[20,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[21,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[22,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[23,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[24,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[25,2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[1,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[2,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[3,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[4,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[5,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[6,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[7,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[8,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[9,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[10,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[11,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[12,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[13,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[14,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[15,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[16,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[17,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[18,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[19,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[20,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[21,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[22,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[23,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[24,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[25,3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[1,1,2] | 0.191 | 0.067 | 0.066 | 0.143 | 0.188 | 0.235 | 0.333 | 1.01 | 1100 |
| gamma[2,1,2] | 0.147 | 0.054 | 0.052 | 0.108 | 0.144 | 0.181 | 0.268 | 1.00 | 4000 |
| gamma[3,1,2] | 0.346 | 0.091 | 0.178 | 0.280 | 0.339 | 0.409 | 0.536 | 1.01 | 280 |
| gamma[4,1,2] | 0.337 | 0.108 | 0.124 | 0.262 | 0.340 | 0.412 | 0.540 | 1.00 | 750 |
| gamma[5,1,2] | 0.218 | 0.081 | 0.062 | 0.163 | 0.214 | 0.271 | 0.381 | 1.01 | 1800 |
| gamma[6,1,2] | 0.226 | 0.086 | 0.071 | 0.163 | 0.224 | 0.282 | 0.404 | 1.01 | 430 |
| gamma[7,1,2] | 0.173 | 0.067 | 0.053 | 0.125 | 0.170 | 0.214 | 0.315 | 1.08 | 88 |
| gamma[8,1,2] | 0.190 | 0.099 | 0.012 | 0.119 | 0.185 | 0.254 | 0.393 | 1.11 | 91 |
| gamma[9,1,2] | 0.123 | 0.114 | 0.003 | 0.038 | 0.089 | 0.172 | 0.412 | 1.02 | 350 |
| gamma[10,1,2] | 0.159 | 0.113 | 0.007 | 0.070 | 0.136 | 0.230 | 0.428 | 1.02 | 270 |
| gamma[11,1,2] | 0.751 | 0.060 | 0.628 | 0.713 | 0.753 | 0.792 | 0.864 | 1.00 | 4000 |
| gamma[12,1,2] | 0.026 | 0.026 | 0.001 | 0.008 | 0.018 | 0.036 | 0.099 | 1.01 | 450 |
| gamma[13,1,2] | 0.026 | 0.026 | 0.001 | 0.008 | 0.019 | 0.037 | 0.097 | 1.00 | 3100 |
| gamma[14,1,2] | 0.346 | 0.125 | 0.096 | 0.259 | 0.346 | 0.434 | 0.591 | 1.00 | 610 |
| gamma[15,1,2] | 0.135 | 0.104 | 0.003 | 0.047 | 0.113 | 0.200 | 0.377 | 1.01 | 400 |
| gamma[16,1,2] | 0.346 | 0.111 | 0.150 | 0.267 | 0.342 | 0.418 | 0.582 | 1.00 | 830 |
| gamma[17,1,2] | 0.263 | 0.100 | 0.087 | 0.194 | 0.258 | 0.330 | 0.475 | 1.01 | 330 |
| gamma[18,1,2] | 0.229 | 0.104 | 0.046 | 0.154 | 0.218 | 0.295 | 0.451 | 1.03 | 140 |
| gamma[19,1,2] | 0.029 | 0.027 | 0.001 | 0.009 | 0.020 | 0.040 | 0.100 | 1.01 | 590 |
| gamma[20,1,2] | 0.057 | 0.041 | 0.003 | 0.024 | 0.050 | 0.082 | 0.156 | 1.01 | 550 |
| gamma[21,1,2] | 0.053 | 0.048 | 0.002 | 0.018 | 0.040 | 0.072 | 0.175 | 1.01 | 4000 |
| gamma[22,1,2] | 0.019 | 0.019 | 0.000 | 0.006 | 0.014 | 0.027 | 0.070 | 1.00 | 2300 |
| gamma[23,1,2] | 0.890 | 0.039 | 0.805 | 0.865 | 0.894 | 0.919 | 0.955 | 1.00 | 1900 |
| gamma[24,1,2] | 0.025 | 0.024 | 0.001 | 0.008 | 0.019 | 0.035 | 0.087 | 1.00 | 1100 |
| gamma[25,1,2] | 0.861 | 0.037 | 0.781 | 0.838 | 0.864 | 0.887 | 0.926 | 1.00 | 560 |
| gamma[1,2,2] | 0.905 | 0.078 | 0.711 | 0.862 | 0.926 | 0.966 | 0.997 | 1.00 | 1400 |
| gamma[2,2,2] | 0.883 | 0.079 | 0.700 | 0.836 | 0.896 | 0.943 | 0.993 | 1.00 | 2300 |
| gamma[3,2,2] | 0.565 | 0.105 | 0.371 | 0.491 | 0.560 | 0.630 | 0.781 | 1.00 | 740 |
| gamma[4,2,2] | 0.837 | 0.110 | 0.582 | 0.766 | 0.854 | 0.925 | 0.991 | 1.00 | 540 |
| gamma[5,2,2] | 0.813 | 0.110 | 0.572 | 0.737 | 0.819 | 0.899 | 0.988 | 1.00 | 1700 |
| gamma[6,2,2] | 0.726 | 0.123 | 0.500 | 0.635 | 0.725 | 0.821 | 0.958 | 1.01 | 460 |
| gamma[7,2,2] | 0.508 | 0.113 | 0.297 | 0.427 | 0.503 | 0.583 | 0.744 | 1.02 | 140 |
| gamma[8,2,2] | 0.847 | 0.093 | 0.638 | 0.787 | 0.857 | 0.920 | 0.988 | 1.00 | 1000 |
| gamma[9,2,2] | 0.786 | 0.099 | 0.572 | 0.725 | 0.795 | 0.856 | 0.958 | 1.00 | 3400 |
| gamma[10,2,2] | 0.938 | 0.054 | 0.808 | 0.912 | 0.952 | 0.979 | 0.998 | 1.00 | 740 |
| gamma[11,2,2] | 0.622 | 0.053 | 0.518 | 0.586 | 0.621 | 0.658 | 0.727 | 1.00 | 3100 |
| gamma[12,2,2] | 0.952 | 0.038 | 0.853 | 0.931 | 0.961 | 0.982 | 0.998 | 1.00 | 4000 |
| gamma[13,2,2] | 0.948 | 0.042 | 0.842 | 0.926 | 0.958 | 0.981 | 0.998 | 1.00 | 4000 |
| gamma[14,2,2] | 0.210 | 0.047 | 0.128 | 0.176 | 0.208 | 0.240 | 0.309 | 1.00 | 1200 |
| gamma[15,2,2] | 0.597 | 0.153 | 0.316 | 0.487 | 0.588 | 0.701 | 0.907 | 1.00 | 770 |
| gamma[16,2,2] | 0.092 | 0.025 | 0.050 | 0.074 | 0.090 | 0.108 | 0.150 | 1.00 | 1300 |
| gamma[17,2,2] | 0.295 | 0.069 | 0.175 | 0.245 | 0.292 | 0.339 | 0.445 | 1.00 | 590 |
| gamma[18,2,2] | 0.285 | 0.065 | 0.172 | 0.238 | 0.279 | 0.328 | 0.425 | 1.01 | 290 |
| gamma[19,2,2] | 0.970 | 0.029 | 0.890 | 0.958 | 0.979 | 0.991 | 0.999 | 1.00 | 1100 |
| gamma[20,2,2] | 0.934 | 0.053 | 0.802 | 0.906 | 0.946 | 0.975 | 0.998 | 1.02 | 220 |
| gamma[21,2,2] | 0.953 | 0.042 | 0.840 | 0.936 | 0.965 | 0.985 | 0.998 | 1.00 | 4000 |
| gamma[22,2,2] | 0.942 | 0.045 | 0.830 | 0.919 | 0.951 | 0.977 | 0.997 | 1.00 | 1100 |
| gamma[23,2,2] | 0.750 | 0.063 | 0.634 | 0.705 | 0.749 | 0.794 | 0.876 | 1.00 | 2300 |
| gamma[24,2,2] | 0.944 | 0.050 | 0.811 | 0.920 | 0.958 | 0.982 | 0.998 | 1.00 | 4000 |
| gamma[25,2,2] | 0.541 | 0.053 | 0.439 | 0.504 | 0.542 | 0.576 | 0.644 | 1.00 | 2200 |
| gamma[1,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[2,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[3,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[4,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[5,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[6,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[7,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[8,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[9,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[10,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[11,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[12,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[13,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[14,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[15,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[16,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[17,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[18,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[19,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[20,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[21,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[22,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[23,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[24,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[25,3,2] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| gamma[1,1,3] | 0.021 | 0.031 | 0.000 | 0.002 | 0.009 | 0.028 | 0.111 | 1.01 | 330 |
| gamma[2,1,3] | 0.023 | 0.029 | 0.000 | 0.004 | 0.013 | 0.032 | 0.102 | 1.03 | 170 |
| gamma[3,1,3] | 0.035 | 0.046 | 0.000 | 0.004 | 0.017 | 0.047 | 0.169 | 1.02 | 280 |
| gamma[4,1,3] | 0.075 | 0.063 | 0.001 | 0.023 | 0.060 | 0.114 | 0.229 | 1.03 | 140 |
| gamma[5,1,3] | 0.020 | 0.029 | 0.000 | 0.002 | 0.008 | 0.025 | 0.103 | 1.09 | 56 |
| gamma[6,1,3] | 0.018 | 0.023 | 0.000 | 0.002 | 0.010 | 0.025 | 0.081 | 1.01 | 200 |
| gamma[7,1,3] | 0.029 | 0.035 | 0.000 | 0.005 | 0.017 | 0.040 | 0.128 | 1.06 | 57 |
| gamma[8,1,3] | 0.046 | 0.051 | 0.000 | 0.007 | 0.029 | 0.068 | 0.185 | 1.11 | 45 |
| gamma[9,1,3] | 0.015 | 0.020 | 0.000 | 0.002 | 0.007 | 0.022 | 0.067 | 1.01 | 460 |
| gamma[10,1,3] | 0.065 | 0.060 | 0.000 | 0.015 | 0.049 | 0.098 | 0.217 | 1.02 | 170 |
| gamma[11,1,3] | 0.016 | 0.017 | 0.000 | 0.002 | 0.010 | 0.024 | 0.062 | 1.05 | 110 |
| gamma[12,1,3] | 0.017 | 0.022 | 0.000 | 0.002 | 0.009 | 0.024 | 0.081 | 1.00 | 1300 |
| gamma[13,1,3] | 0.011 | 0.015 | 0.000 | 0.001 | 0.005 | 0.015 | 0.054 | 1.03 | 150 |
| gamma[14,1,3] | 0.026 | 0.033 | 0.000 | 0.003 | 0.013 | 0.035 | 0.119 | 1.02 | 240 |
| gamma[15,1,3] | 0.045 | 0.055 | 0.000 | 0.007 | 0.024 | 0.063 | 0.211 | 1.01 | 390 |
| gamma[16,1,3] | 0.024 | 0.031 | 0.000 | 0.004 | 0.012 | 0.032 | 0.117 | 1.03 | 110 |
| gamma[17,1,3] | 0.038 | 0.044 | 0.000 | 0.006 | 0.021 | 0.055 | 0.157 | 1.03 | 180 |
| gamma[18,1,3] | 0.021 | 0.030 | 0.000 | 0.001 | 0.008 | 0.028 | 0.105 | 1.11 | 63 |
| gamma[19,1,3] | 0.019 | 0.022 | 0.000 | 0.003 | 0.011 | 0.027 | 0.082 | 1.03 | 150 |
| gamma[20,1,3] | 0.076 | 0.060 | 0.001 | 0.028 | 0.063 | 0.112 | 0.214 | 1.01 | 540 |
| gamma[21,1,3] | 0.067 | 0.052 | 0.001 | 0.027 | 0.058 | 0.098 | 0.188 | 1.02 | 520 |
| gamma[22,1,3] | 0.010 | 0.014 | 0.000 | 0.001 | 0.004 | 0.013 | 0.050 | 1.12 | 63 |
| gamma[23,1,3] | 0.004 | 0.006 | 0.000 | 0.001 | 0.002 | 0.006 | 0.021 | 1.06 | 340 |
| gamma[24,1,3] | 0.019 | 0.026 | 0.000 | 0.002 | 0.009 | 0.026 | 0.097 | 1.01 | 280 |
| gamma[25,1,3] | 0.006 | 0.008 | 0.000 | 0.001 | 0.003 | 0.008 | 0.029 | 1.02 | 250 |
| gamma[1,2,3] | 0.095 | 0.078 | 0.003 | 0.034 | 0.074 | 0.138 | 0.289 | 1.00 | 1600 |
| gamma[2,2,3] | 0.117 | 0.079 | 0.007 | 0.057 | 0.104 | 0.164 | 0.300 | 1.00 | 4000 |
| gamma[3,2,3] | 0.435 | 0.105 | 0.219 | 0.370 | 0.440 | 0.509 | 0.629 | 1.01 | 750 |
| gamma[4,2,3] | 0.163 | 0.110 | 0.009 | 0.075 | 0.146 | 0.234 | 0.418 | 1.01 | 550 |
| gamma[5,2,3] | 0.187 | 0.110 | 0.012 | 0.101 | 0.181 | 0.263 | 0.428 | 1.00 | 970 |
| gamma[6,2,3] | 0.274 | 0.123 | 0.042 | 0.179 | 0.275 | 0.365 | 0.500 | 1.01 | 430 |
| gamma[7,2,3] | 0.492 | 0.113 | 0.256 | 0.417 | 0.497 | 0.573 | 0.703 | 1.01 | 220 |
| gamma[8,2,3] | 0.153 | 0.093 | 0.012 | 0.080 | 0.143 | 0.213 | 0.362 | 1.00 | 1100 |
| gamma[9,2,3] | 0.214 | 0.099 | 0.042 | 0.144 | 0.205 | 0.275 | 0.428 | 1.01 | 1200 |
| gamma[10,2,3] | 0.062 | 0.054 | 0.002 | 0.021 | 0.048 | 0.088 | 0.192 | 1.00 | 830 |
| gamma[11,2,3] | 0.378 | 0.053 | 0.273 | 0.342 | 0.379 | 0.414 | 0.482 | 1.00 | 3300 |
| gamma[12,2,3] | 0.048 | 0.038 | 0.002 | 0.018 | 0.039 | 0.069 | 0.147 | 1.00 | 910 |
| gamma[13,2,3] | 0.052 | 0.042 | 0.002 | 0.019 | 0.042 | 0.074 | 0.158 | 1.00 | 4000 |
| gamma[14,2,3] | 0.790 | 0.047 | 0.691 | 0.760 | 0.792 | 0.824 | 0.872 | 1.00 | 1100 |
| gamma[15,2,3] | 0.403 | 0.153 | 0.093 | 0.299 | 0.412 | 0.513 | 0.684 | 1.01 | 770 |
| gamma[16,2,3] | 0.908 | 0.025 | 0.850 | 0.892 | 0.910 | 0.926 | 0.950 | 1.00 | 1500 |
| gamma[17,2,3] | 0.705 | 0.069 | 0.555 | 0.661 | 0.708 | 0.755 | 0.825 | 1.00 | 640 |
| gamma[18,2,3] | 0.715 | 0.065 | 0.575 | 0.672 | 0.721 | 0.762 | 0.828 | 1.01 | 310 |
| gamma[19,2,3] | 0.030 | 0.029 | 0.001 | 0.009 | 0.021 | 0.042 | 0.110 | 1.00 | 940 |
| gamma[20,2,3] | 0.066 | 0.053 | 0.002 | 0.025 | 0.054 | 0.094 | 0.198 | 1.01 | 390 |
| gamma[21,2,3] | 0.047 | 0.042 | 0.002 | 0.015 | 0.035 | 0.064 | 0.160 | 1.00 | 2700 |
| gamma[22,2,3] | 0.058 | 0.045 | 0.003 | 0.023 | 0.049 | 0.081 | 0.170 | 1.01 | 370 |
| gamma[23,2,3] | 0.250 | 0.063 | 0.124 | 0.206 | 0.251 | 0.295 | 0.366 | 1.00 | 4000 |
| gamma[24,2,3] | 0.056 | 0.050 | 0.002 | 0.018 | 0.042 | 0.080 | 0.189 | 1.00 | 2800 |
| gamma[25,2,3] | 0.459 | 0.053 | 0.356 | 0.424 | 0.458 | 0.496 | 0.561 | 1.00 | 1900 |
| gamma[1,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[2,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[3,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[4,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[5,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[6,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[7,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[8,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[9,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[10,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[11,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[12,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[13,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[14,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[15,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[16,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[17,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[18,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[19,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[20,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[21,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[22,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[23,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[24,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| gamma[25,3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| inv.phi[1,1] | 3.199 | 1.546 | 0.898 | 2.039 | 2.957 | 4.082 | 6.881 | 1.03 | 110 |
| inv.phi[2,1] | -0.518 | 1.063 | -2.782 | -1.166 | -0.502 | 0.173 | 1.566 | 1.05 | 53 |
| inv.phi[3,1] | -1.166 | 1.121 | -3.742 | -1.794 | -1.040 | -0.415 | 0.718 | 1.06 | 54 |
| inv.phi[4,1] | -1.191 | 1.351 | -4.239 | -1.975 | -1.037 | -0.236 | 0.988 | 1.04 | 68 |
| inv.phi[1,2] | -0.518 | 1.063 | -2.782 | -1.166 | -0.502 | 0.173 | 1.566 | 1.05 | 53 |
| inv.phi[2,2] | 2.927 | 1.511 | 0.675 | 1.831 | 2.641 | 3.788 | 6.543 | 1.10 | 34 |
| inv.phi[3,2] | -0.100 | 0.945 | -2.180 | -0.634 | -0.064 | 0.502 | 1.649 | 1.03 | 82 |
| inv.phi[4,2] | -1.998 | 1.420 | -5.256 | -2.807 | -1.752 | -0.934 | 0.068 | 1.05 | 62 |
| inv.phi[1,3] | -1.166 | 1.121 | -3.742 | -1.794 | -1.040 | -0.415 | 0.718 | 1.06 | 54 |
| inv.phi[2,3] | -0.100 | 0.945 | -2.180 | -0.634 | -0.064 | 0.502 | 1.649 | 1.03 | 82 |
| inv.phi[3,3] | 2.600 | 1.321 | 0.705 | 1.600 | 2.389 | 3.316 | 5.707 | 1.05 | 59 |
| inv.phi[4,3] | -0.823 | 1.267 | -3.622 | -1.597 | -0.689 | 0.099 | 1.335 | 1.05 | 65 |
| inv.phi[1,4] | -1.191 | 1.351 | -4.239 | -1.975 | -1.037 | -0.236 | 0.988 | 1.04 | 68 |
| inv.phi[2,4] | -1.998 | 1.420 | -5.256 | -2.807 | -1.752 | -0.934 | 0.068 | 1.05 | 62 |
| inv.phi[3,4] | -0.823 | 1.267 | -3.622 | -1.597 | -0.689 | 0.099 | 1.335 | 1.05 | 65 |
| inv.phi[4,4] | 3.886 | 2.180 | 0.770 | 2.237 | 3.498 | 5.155 | 9.043 | 1.03 | 95 |
| lambda[1] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[2] | 1.459 | 0.182 | 1.127 | 1.330 | 1.447 | 1.579 | 1.842 | 1.01 | 620 |
| lambda[3] | 1.359 | 0.178 | 1.047 | 1.234 | 1.344 | 1.471 | 1.735 | 1.01 | 460 |
| lambda[4] | 1.014 | 0.130 | 0.764 | 0.928 | 1.008 | 1.097 | 1.291 | 1.02 | 100 |
| lambda[5] | 1.127 | 0.125 | 0.904 | 1.040 | 1.122 | 1.212 | 1.384 | 1.01 | 500 |
| lambda[6] | 1.086 | 0.135 | 0.835 | 0.993 | 1.084 | 1.176 | 1.361 | 1.01 | 240 |
| lambda[7] | 1.415 | 0.184 | 1.098 | 1.281 | 1.401 | 1.537 | 1.796 | 1.01 | 330 |
| lambda[8] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[9] | 0.864 | 0.094 | 0.688 | 0.799 | 0.861 | 0.926 | 1.052 | 1.02 | 140 |
| lambda[10] | 0.756 | 0.095 | 0.585 | 0.690 | 0.749 | 0.817 | 0.962 | 1.01 | 230 |
| lambda[11] | 0.763 | 0.101 | 0.578 | 0.692 | 0.758 | 0.828 | 0.974 | 1.01 | 290 |
| lambda[12] | 0.923 | 0.088 | 0.767 | 0.861 | 0.920 | 0.980 | 1.108 | 1.01 | 290 |
| lambda[13] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[14] | 0.827 | 0.130 | 0.576 | 0.740 | 0.823 | 0.915 | 1.086 | 1.02 | 110 |
| lambda[15] | 0.490 | 0.074 | 0.358 | 0.439 | 0.485 | 0.537 | 0.646 | 1.02 | 180 |
| lambda[16] | 1.398 | 0.247 | 0.963 | 1.227 | 1.384 | 1.559 | 1.917 | 1.02 | 120 |
| lambda[17] | 1.295 | 0.209 | 0.927 | 1.136 | 1.281 | 1.452 | 1.697 | 1.04 | 71 |
| lambda[18] | 0.907 | 0.139 | 0.657 | 0.811 | 0.900 | 0.993 | 1.206 | 1.02 | 160 |
| lambda[19] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| lambda[20] | 1.197 | 0.129 | 0.969 | 1.107 | 1.190 | 1.282 | 1.472 | 1.01 | 760 |
| lambda[21] | 0.957 | 0.102 | 0.769 | 0.884 | 0.952 | 1.024 | 1.165 | 1.00 | 870 |
| lambda[22] | 1.111 | 0.101 | 0.925 | 1.041 | 1.108 | 1.175 | 1.319 | 1.01 | 240 |
| lambda[23] | 0.935 | 0.112 | 0.731 | 0.857 | 0.928 | 1.005 | 1.179 | 1.01 | 270 |
| lambda[24] | 0.911 | 0.090 | 0.754 | 0.847 | 0.903 | 0.965 | 1.109 | 1.01 | 430 |
| lambda[25] | 0.840 | 0.101 | 0.655 | 0.770 | 0.836 | 0.904 | 1.055 | 1.01 | 250 |
| lambda.std[1] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[2] | 0.821 | 0.033 | 0.748 | 0.799 | 0.823 | 0.845 | 0.879 | 1.01 | 840 |
| lambda.std[3] | 0.801 | 0.037 | 0.723 | 0.777 | 0.802 | 0.827 | 0.866 | 1.01 | 390 |
| lambda.std[4] | 0.708 | 0.045 | 0.607 | 0.680 | 0.710 | 0.739 | 0.791 | 1.02 | 110 |
| lambda.std[5] | 0.745 | 0.037 | 0.671 | 0.721 | 0.747 | 0.771 | 0.810 | 1.01 | 420 |
| lambda.std[6] | 0.731 | 0.042 | 0.641 | 0.705 | 0.735 | 0.762 | 0.806 | 1.01 | 270 |
| lambda.std[7] | 0.812 | 0.036 | 0.739 | 0.788 | 0.814 | 0.838 | 0.874 | 1.01 | 290 |
| lambda.std[8] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[9] | 0.651 | 0.041 | 0.567 | 0.624 | 0.652 | 0.680 | 0.725 | 1.02 | 140 |
| lambda.std[10] | 0.600 | 0.048 | 0.505 | 0.568 | 0.599 | 0.633 | 0.693 | 1.02 | 210 |
| lambda.std[11] | 0.603 | 0.050 | 0.500 | 0.569 | 0.604 | 0.638 | 0.698 | 1.01 | 290 |
| lambda.std[12] | 0.676 | 0.035 | 0.609 | 0.652 | 0.677 | 0.700 | 0.742 | 1.01 | 290 |
| lambda.std[13] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[14] | 0.632 | 0.060 | 0.499 | 0.595 | 0.635 | 0.675 | 0.736 | 1.03 | 110 |
| lambda.std[15] | 0.438 | 0.053 | 0.337 | 0.402 | 0.436 | 0.473 | 0.542 | 1.02 | 180 |
| lambda.std[16] | 0.805 | 0.050 | 0.694 | 0.775 | 0.811 | 0.842 | 0.887 | 1.02 | 140 |
| lambda.std[17] | 0.784 | 0.049 | 0.680 | 0.751 | 0.788 | 0.824 | 0.862 | 1.04 | 79 |
| lambda.std[18] | 0.666 | 0.056 | 0.549 | 0.630 | 0.669 | 0.705 | 0.770 | 1.03 | 140 |
| lambda.std[19] | 0.707 | 0.000 | 0.707 | 0.707 | 0.707 | 0.707 | 0.707 | 1.00 | 1 |
| lambda.std[20] | 0.764 | 0.034 | 0.696 | 0.742 | 0.765 | 0.789 | 0.827 | 1.01 | 820 |
| lambda.std[21] | 0.688 | 0.038 | 0.610 | 0.662 | 0.690 | 0.715 | 0.759 | 1.00 | 830 |
| lambda.std[22] | 0.741 | 0.030 | 0.679 | 0.721 | 0.742 | 0.762 | 0.797 | 1.01 | 220 |
| lambda.std[23] | 0.679 | 0.043 | 0.590 | 0.651 | 0.680 | 0.709 | 0.763 | 1.01 | 270 |
| lambda.std[24] | 0.671 | 0.036 | 0.602 | 0.646 | 0.670 | 0.694 | 0.743 | 1.01 | 420 |
| lambda.std[25] | 0.640 | 0.045 | 0.548 | 0.610 | 0.641 | 0.671 | 0.726 | 1.01 | 240 |
| phi[1,1] | 2.590 | 1.414 | 0.715 | 1.511 | 2.328 | 3.377 | 6.130 | 1.01 | 580 |
| phi[2,1] | 2.025 | 1.217 | 0.210 | 1.174 | 1.873 | 2.761 | 4.778 | 1.04 | 110 |
| phi[3,1] | 1.865 | 1.277 | 0.004 | 1.029 | 1.679 | 2.467 | 4.959 | 1.03 | 210 |
| phi[4,1] | 2.155 | 0.963 | 0.249 | 1.511 | 2.171 | 2.824 | 4.002 | 1.01 | 400 |
| phi[1,2] | 2.025 | 1.217 | 0.210 | 1.174 | 1.873 | 2.761 | 4.778 | 1.04 | 110 |
| phi[2,2] | 3.217 | 2.517 | 0.965 | 1.891 | 2.635 | 3.774 | 9.479 | 1.13 | 32 |
| phi[3,2] | 1.776 | 1.279 | -0.596 | 1.029 | 1.731 | 2.471 | 4.346 | 1.04 | 180 |
| phi[4,2] | 2.525 | 0.954 | 0.730 | 1.921 | 2.469 | 3.092 | 4.438 | 1.09 | 46 |
| phi[1,3] | 1.865 | 1.277 | 0.004 | 1.029 | 1.679 | 2.467 | 4.959 | 1.03 | 210 |
| phi[2,3] | 1.776 | 1.279 | -0.596 | 1.029 | 1.731 | 2.471 | 4.346 | 1.04 | 180 |
| phi[3,3] | 2.586 | 1.680 | 0.702 | 1.541 | 2.233 | 3.137 | 6.440 | 1.04 | 120 |
| phi[4,3] | 1.914 | 1.134 | -0.748 | 1.340 | 2.061 | 2.620 | 3.852 | 1.03 | 370 |
| phi[1,4] | 2.155 | 0.963 | 0.249 | 1.511 | 2.171 | 2.824 | 4.002 | 1.01 | 400 |
| phi[2,4] | 2.525 | 0.954 | 0.730 | 1.921 | 2.469 | 3.092 | 4.438 | 1.09 | 46 |
| phi[3,4] | 1.914 | 1.134 | -0.748 | 1.340 | 2.061 | 2.620 | 3.852 | 1.03 | 370 |
| phi[4,4] | 2.958 | 0.307 | 2.408 | 2.740 | 2.942 | 3.166 | 3.592 | 1.01 | 220 |
| phi.cor[1,1] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[2,1] | 0.732 | 0.223 | 0.133 | 0.656 | 0.804 | 0.883 | 0.951 | 1.07 | 100 |
| phi.cor[3,1] | 0.721 | 0.241 | 0.003 | 0.646 | 0.793 | 0.884 | 0.955 | 1.02 | 170 |
| phi.cor[4,1] | 0.779 | 0.214 | 0.121 | 0.735 | 0.855 | 0.912 | 0.960 | 1.07 | 120 |
| phi.cor[1,2] | 0.732 | 0.223 | 0.133 | 0.656 | 0.804 | 0.883 | 0.951 | 1.07 | 100 |
| phi.cor[2,2] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[3,2] | 0.651 | 0.299 | -0.245 | 0.566 | 0.757 | 0.848 | 0.930 | 1.05 | 170 |
| phi.cor[4,2] | 0.843 | 0.153 | 0.397 | 0.816 | 0.893 | 0.933 | 0.968 | 1.04 | 160 |
| phi.cor[1,3] | 0.721 | 0.241 | 0.003 | 0.646 | 0.793 | 0.884 | 0.955 | 1.02 | 170 |
| phi.cor[2,3] | 0.651 | 0.299 | -0.245 | 0.566 | 0.757 | 0.848 | 0.930 | 1.05 | 170 |
| phi.cor[3,3] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| phi.cor[4,3] | 0.698 | 0.321 | -0.348 | 0.655 | 0.818 | 0.892 | 0.947 | 1.06 | 97 |
| phi.cor[1,4] | 0.779 | 0.214 | 0.121 | 0.735 | 0.855 | 0.912 | 0.960 | 1.07 | 120 |
| phi.cor[2,4] | 0.843 | 0.153 | 0.397 | 0.816 | 0.893 | 0.933 | 0.968 | 1.04 | 160 |
| phi.cor[3,4] | 0.698 | 0.321 | -0.348 | 0.655 | 0.818 | 0.892 | 0.947 | 1.06 | 97 |
| phi.cor[4,4] | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.00 | 1 |
| reli.omega[1] | 0.910 | 0.009 | 0.891 | 0.904 | 0.911 | 0.917 | 0.927 | 1.01 | 660 |
| reli.omega[2] | 0.824 | 0.012 | 0.799 | 0.815 | 0.824 | 0.833 | 0.846 | 1.03 | 95 |
| reli.omega[3] | 0.852 | 0.020 | 0.812 | 0.838 | 0.853 | 0.866 | 0.888 | 1.02 | 230 |
| reli.omega[4] | 0.861 | 0.012 | 0.837 | 0.853 | 0.861 | 0.869 | 0.884 | 1.02 | 190 |
| tau[1,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[2,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[3,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[4,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[5,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[6,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[7,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[8,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[9,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[10,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[11,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[12,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[13,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[14,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[15,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[16,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[17,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[18,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[19,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[20,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[21,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[22,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[23,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[24,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[25,1] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.00 | 1 |
| tau[1,2] | 3.126 | 0.166 | 2.802 | 3.013 | 3.125 | 3.242 | 3.455 | 1.00 | 890 |
| tau[2,2] | 4.009 | 0.364 | 3.375 | 3.754 | 3.987 | 4.244 | 4.812 | 1.01 | 230 |
| tau[3,2] | 3.623 | 0.317 | 3.038 | 3.399 | 3.610 | 3.831 | 4.283 | 1.00 | 2500 |
| tau[4,2] | 2.206 | 0.181 | 1.865 | 2.085 | 2.204 | 2.316 | 2.583 | 1.02 | 150 |
| tau[5,2] | 2.736 | 0.210 | 2.348 | 2.591 | 2.726 | 2.871 | 3.163 | 1.01 | 540 |
| tau[6,2] | 3.155 | 0.253 | 2.685 | 2.981 | 3.145 | 3.317 | 3.694 | 1.01 | 420 |
| tau[7,2] | 4.327 | 0.388 | 3.642 | 4.053 | 4.297 | 4.565 | 5.171 | 1.01 | 240 |
| tau[8,2] | 2.049 | 0.130 | 1.796 | 1.961 | 2.049 | 2.137 | 2.308 | 1.00 | 1300 |
| tau[9,2] | 0.955 | 0.141 | 0.656 | 0.869 | 0.965 | 1.054 | 1.198 | 1.00 | 4000 |
| tau[10,2] | 1.510 | 0.115 | 1.289 | 1.430 | 1.508 | 1.587 | 1.744 | 1.00 | 890 |
| tau[11,2] | 0.079 | 0.062 | 0.003 | 0.029 | 0.065 | 0.119 | 0.226 | 1.00 | 4000 |
| tau[12,2] | 1.746 | 0.110 | 1.534 | 1.671 | 1.744 | 1.819 | 1.966 | 1.00 | 680 |
| tau[13,2] | 1.813 | 0.104 | 1.611 | 1.741 | 1.814 | 1.883 | 2.014 | 1.00 | 4000 |
| tau[14,2] | 2.922 | 0.222 | 2.520 | 2.762 | 2.918 | 3.069 | 3.380 | 1.01 | 230 |
| tau[15,2] | 1.424 | 0.137 | 1.167 | 1.330 | 1.423 | 1.516 | 1.701 | 1.00 | 1100 |
| tau[16,2] | 4.979 | 0.535 | 4.054 | 4.596 | 4.942 | 5.324 | 6.106 | 1.03 | 100 |
| tau[17,2] | 3.798 | 0.341 | 3.181 | 3.554 | 3.783 | 4.024 | 4.520 | 1.04 | 81 |
| tau[18,2] | 3.220 | 0.253 | 2.742 | 3.047 | 3.207 | 3.382 | 3.733 | 1.01 | 340 |
| tau[19,2] | 2.147 | 0.115 | 1.926 | 2.069 | 2.146 | 2.227 | 2.371 | 1.00 | 1600 |
| tau[20,2] | 2.988 | 0.208 | 2.608 | 2.844 | 2.972 | 3.119 | 3.424 | 1.00 | 560 |
| tau[21,2] | 1.770 | 0.122 | 1.537 | 1.687 | 1.768 | 1.853 | 2.014 | 1.00 | 2200 |
| tau[22,2] | 2.152 | 0.137 | 1.904 | 2.057 | 2.147 | 2.243 | 2.431 | 1.00 | 1000 |
| tau[23,2] | 0.138 | 0.079 | 0.009 | 0.074 | 0.135 | 0.193 | 0.299 | 1.00 | 4000 |
| tau[24,2] | 1.979 | 0.124 | 1.748 | 1.893 | 1.976 | 2.060 | 2.232 | 1.00 | 2100 |
| tau[25,2] | 0.046 | 0.040 | 0.001 | 0.016 | 0.035 | 0.066 | 0.145 | 1.00 | 1100 |
| theta[1] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[2] | 3.161 | 0.542 | 2.269 | 2.770 | 3.094 | 3.492 | 4.392 | 1.01 | 540 |
| theta[3] | 2.878 | 0.496 | 2.096 | 2.523 | 2.807 | 3.164 | 4.009 | 1.00 | 510 |
| theta[4] | 2.045 | 0.269 | 1.584 | 1.860 | 2.017 | 2.203 | 2.666 | 1.03 | 100 |
| theta[5] | 2.287 | 0.286 | 1.818 | 2.081 | 2.259 | 2.468 | 2.915 | 1.01 | 570 |
| theta[6] | 2.198 | 0.298 | 1.697 | 1.986 | 2.175 | 2.383 | 2.851 | 1.01 | 220 |
| theta[7] | 3.035 | 0.534 | 2.206 | 2.641 | 2.963 | 3.364 | 4.227 | 1.01 | 350 |
| theta[8] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[9] | 1.756 | 0.166 | 1.473 | 1.638 | 1.741 | 1.858 | 2.107 | 1.02 | 140 |
| theta[10] | 1.581 | 0.148 | 1.342 | 1.476 | 1.561 | 1.667 | 1.926 | 1.01 | 270 |
| theta[11] | 1.592 | 0.158 | 1.334 | 1.479 | 1.574 | 1.686 | 1.949 | 1.01 | 290 |
| theta[12] | 1.860 | 0.164 | 1.588 | 1.741 | 1.846 | 1.961 | 2.227 | 1.01 | 280 |
| theta[13] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[14] | 1.702 | 0.219 | 1.332 | 1.547 | 1.677 | 1.838 | 2.179 | 1.02 | 120 |
| theta[15] | 1.246 | 0.075 | 1.128 | 1.192 | 1.235 | 1.289 | 1.417 | 1.02 | 180 |
| theta[16] | 3.016 | 0.714 | 1.928 | 2.504 | 2.915 | 3.431 | 4.677 | 1.03 | 110 |
| theta[17] | 2.720 | 0.553 | 1.860 | 2.291 | 2.640 | 3.109 | 3.881 | 1.04 | 68 |
| theta[18] | 1.842 | 0.263 | 1.432 | 1.657 | 1.810 | 1.987 | 2.455 | 1.02 | 200 |
| theta[19] | 2.000 | 0.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 1.00 | 1 |
| theta[20] | 2.451 | 0.314 | 1.939 | 2.226 | 2.415 | 2.644 | 3.168 | 1.01 | 710 |
| theta[21] | 1.926 | 0.197 | 1.591 | 1.781 | 1.907 | 2.049 | 2.357 | 1.00 | 920 |
| theta[22] | 2.244 | 0.228 | 1.855 | 2.083 | 2.228 | 2.381 | 2.740 | 1.01 | 250 |
| theta[23] | 1.886 | 0.214 | 1.534 | 1.735 | 1.861 | 2.011 | 2.390 | 1.01 | 270 |
| theta[24] | 1.837 | 0.169 | 1.568 | 1.718 | 1.816 | 1.931 | 2.231 | 1.01 | 450 |
| theta[25] | 1.716 | 0.174 | 1.430 | 1.594 | 1.699 | 1.818 | 2.113 | 1.01 | 280 |
Posterior Distribution Summary
# extract for plotting
jags.mcmc <- as.mcmc(model.fit)
a <- colnames(as.data.frame(jags.mcmc[[1]]))
fit.mcmc <- data.frame(as.matrix(jags.mcmc, chains = T, iters = T))
colnames(fit.mcmc) <- c("chain", "iter", a)
fit.mcmc.ggs <- ggmcmc::ggs(jags.mcmc) # for GRB plotFactor Loadings (\(\lambda\))
bayesplot::mcmc_areas(fit.mcmc, regex_pars = "lambda.std", prob = 0.8); ggsave("fig/pools_model3_lambda_dens.pdf")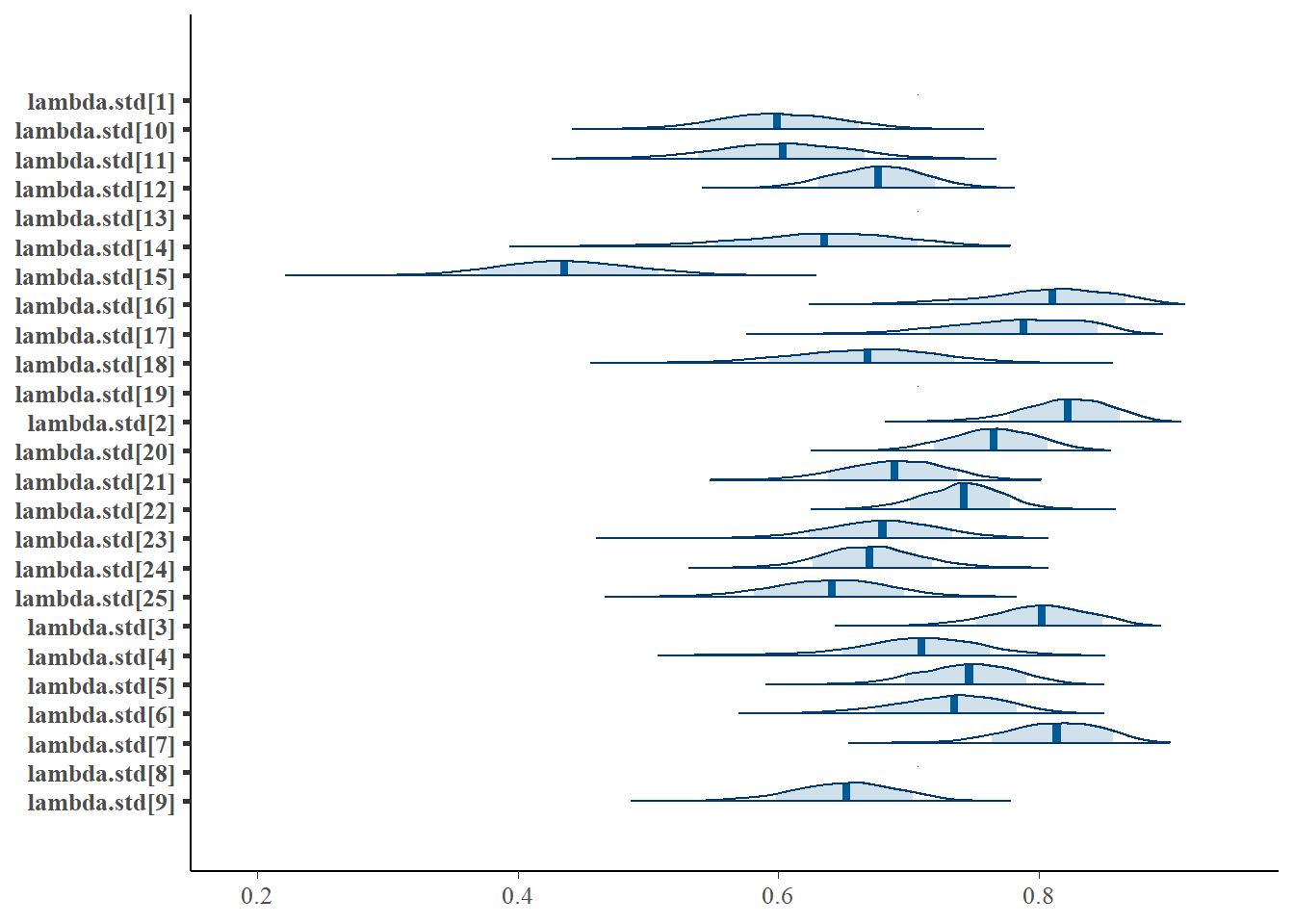
Saving 7 x 5 in imagebayesplot::mcmc_acf(fit.mcmc, regex_pars = "lambda.std"); ggsave("fig/pools_model3_lambda_acf.pdf")Warning: Removed 336 rows containing missing values (geom_segment).Warning: Removed 21 row(s) containing missing values (geom_path).
Saving 7 x 5 in imageWarning: Removed 336 rows containing missing values (geom_segment).
Warning: Removed 21 row(s) containing missing values (geom_path).bayesplot::mcmc_trace(fit.mcmc, regex_pars = "lambda.std"); ggsave("fig/pools_model3_lambda_trace.pdf")
Saving 7 x 5 in imageggmcmc::ggs_grb(fit.mcmc.ggs, family = "lambda.std"); ggsave("fig/pools_model3_lambda_grb.pdf")Warning: Removed 50 row(s) containing missing values (geom_path).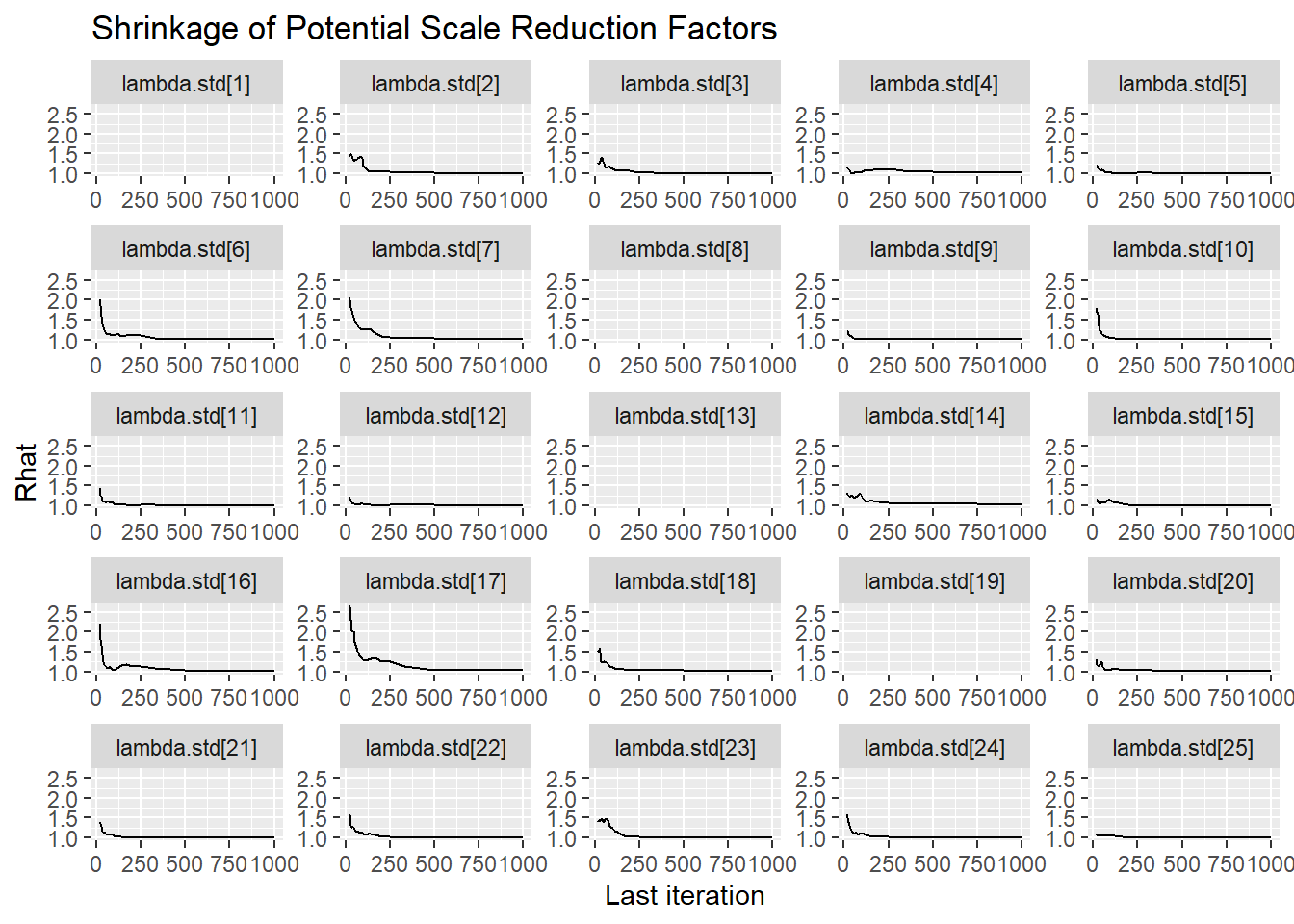
Saving 7 x 5 in imageWarning: Removed 50 row(s) containing missing values (geom_path).Factor Correlations
bayesplot::mcmc_areas(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'), prob = 0.8)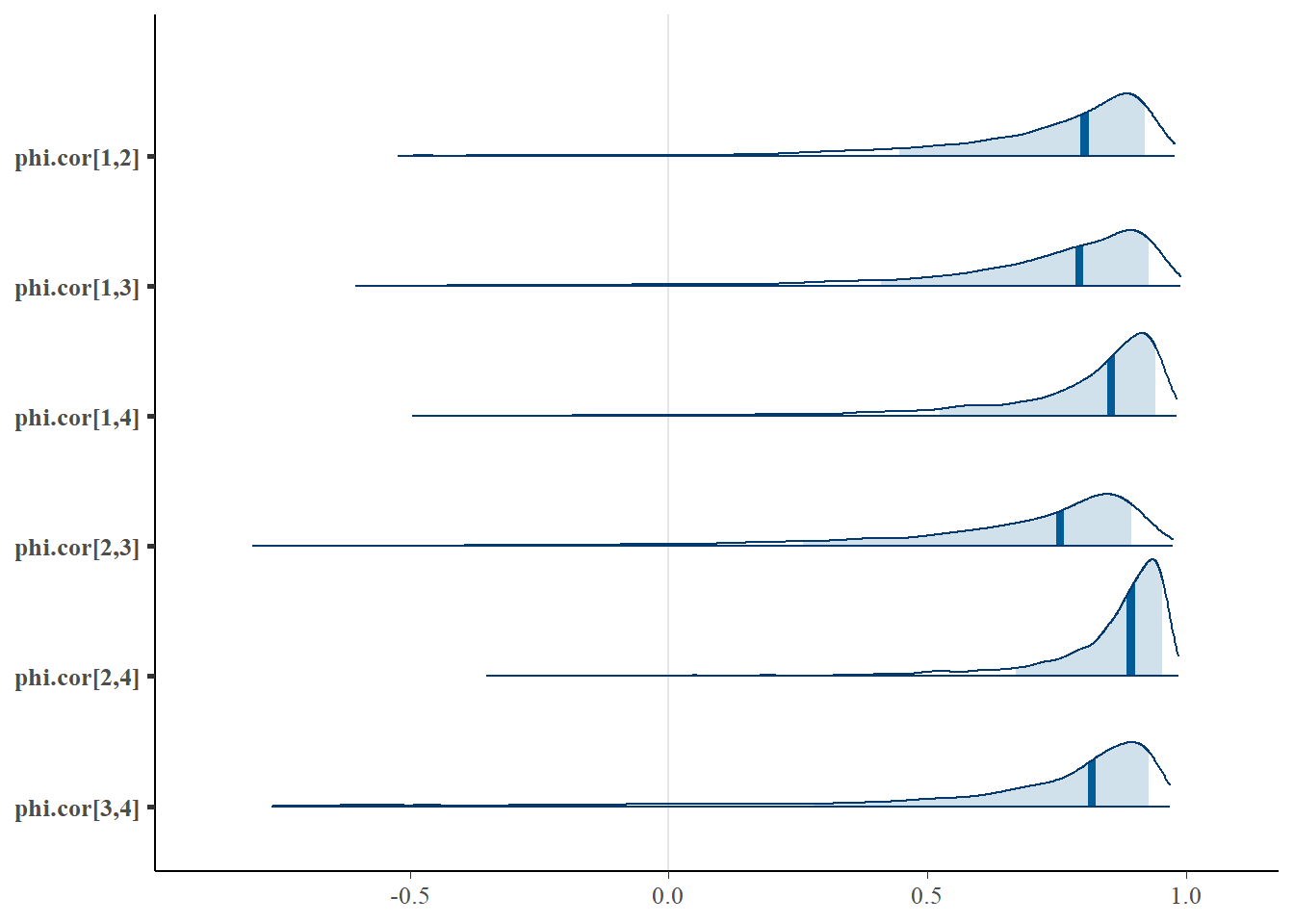
bayesplot::mcmc_acf(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'))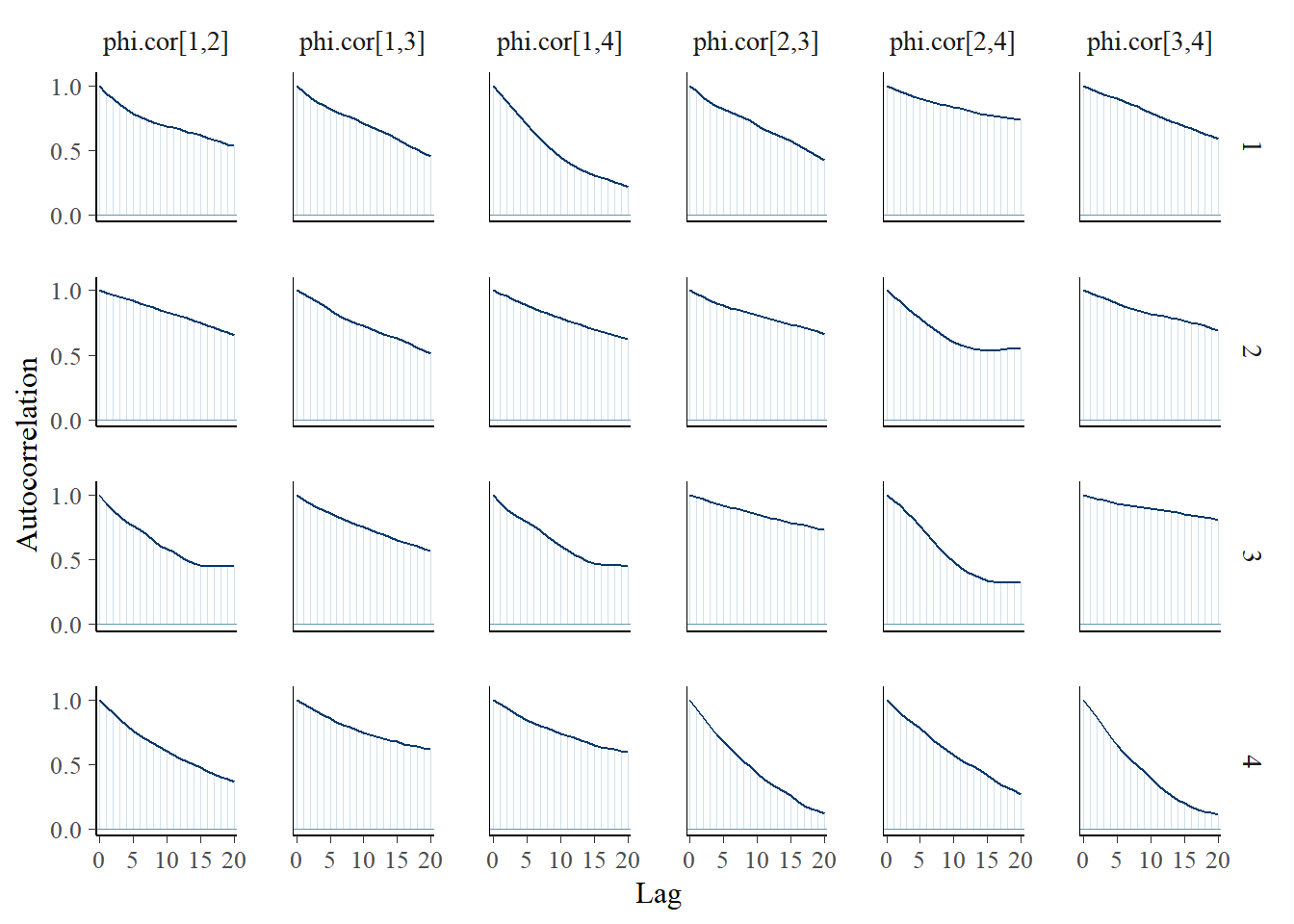
bayesplot::mcmc_trace(
fit.mcmc,
pars = c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]'))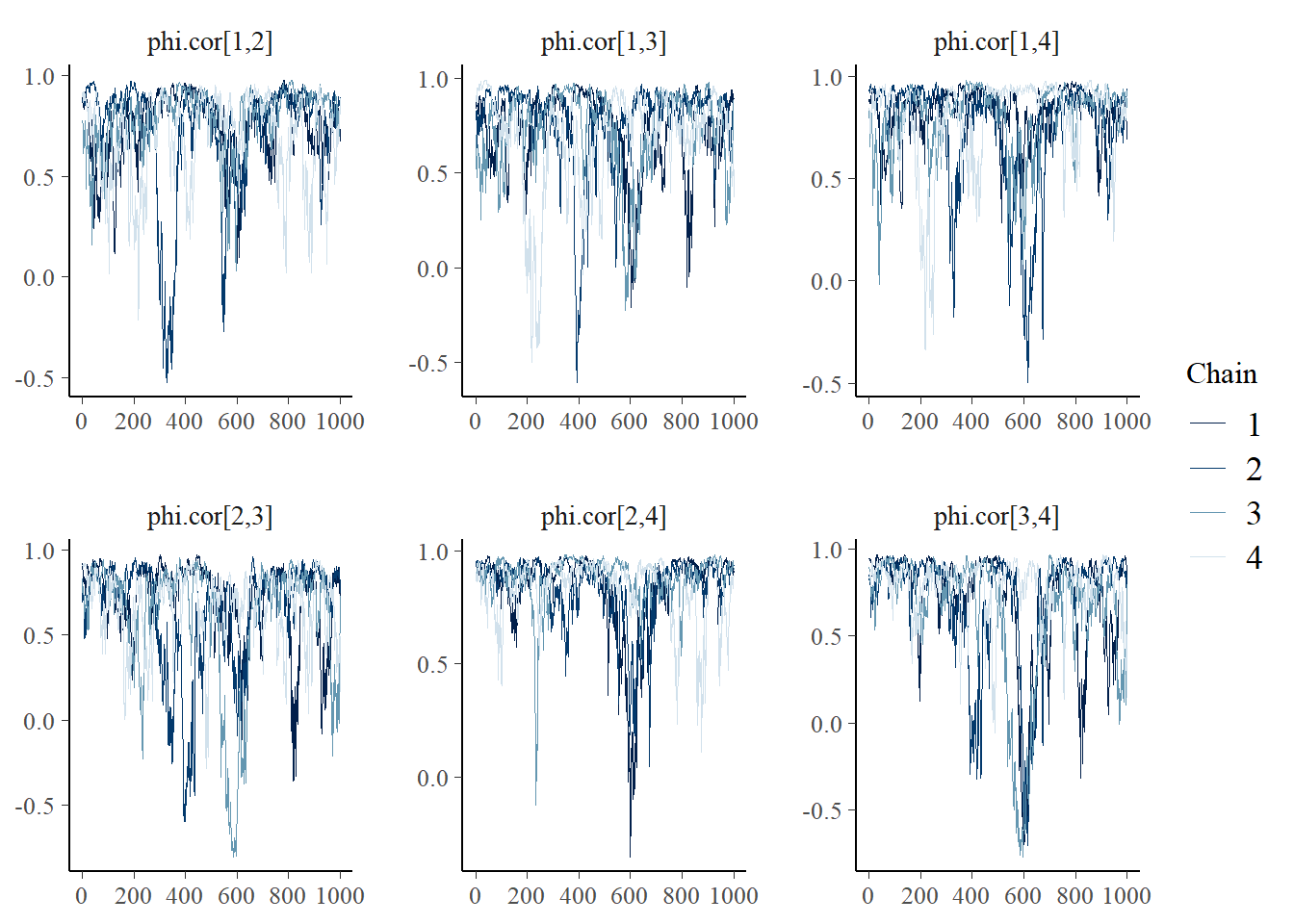
ggmcmc::ggs_grb(fit.mcmc.ggs, family = "phi.cor")Warning: Removed 50 row(s) containing missing values (geom_path).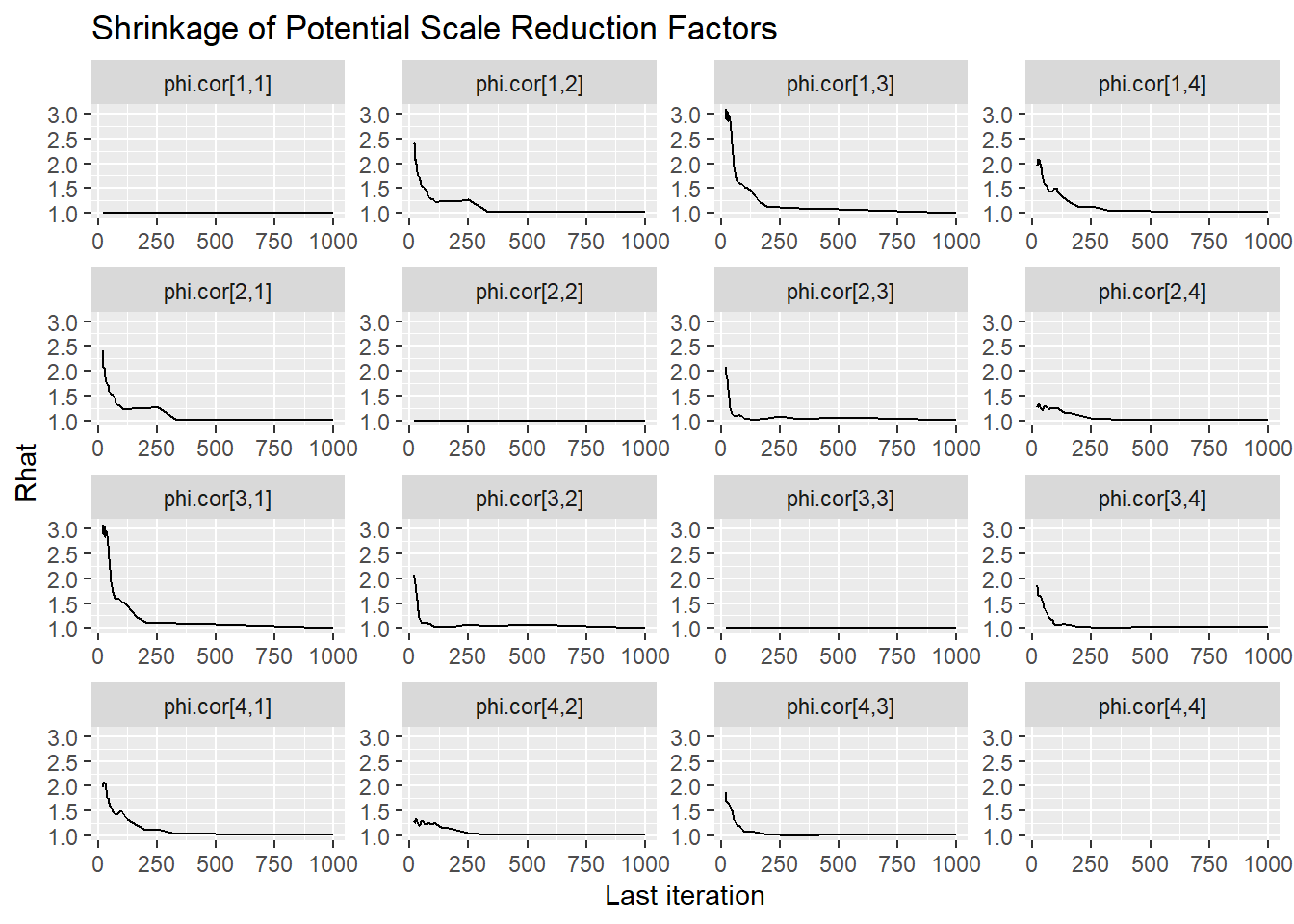
# save factor correlations
use.vars <- c('phi.cor[1,2]', 'phi.cor[1,3]', 'phi.cor[1,4]',
'phi.cor[2,3]', 'phi.cor[2,4]', 'phi.cor[3,4]')
extracted_cor <- fit.mcmc[,use.vars]
write.csv(x=extracted_cor, file=paste0(getwd(),"/data/pools/extracted_cor_m3.csv"))Misclassification
use.vars <- c("gamma[1,1,1]", "gamma[1,1,2]", "gamma[1,1,3]",
"gamma[1,2,1]", "gamma[1,2,2]", "gamma[1,2,3]",
"gamma[1,3,1]", "gamma[1,3,2]", "gamma[1,3,3]")
bayesplot::mcmc_areas(fit.mcmc, pars = use.vars, prob = 0.8); ggsave("fig/pools_model3_gamma_dens.pdf")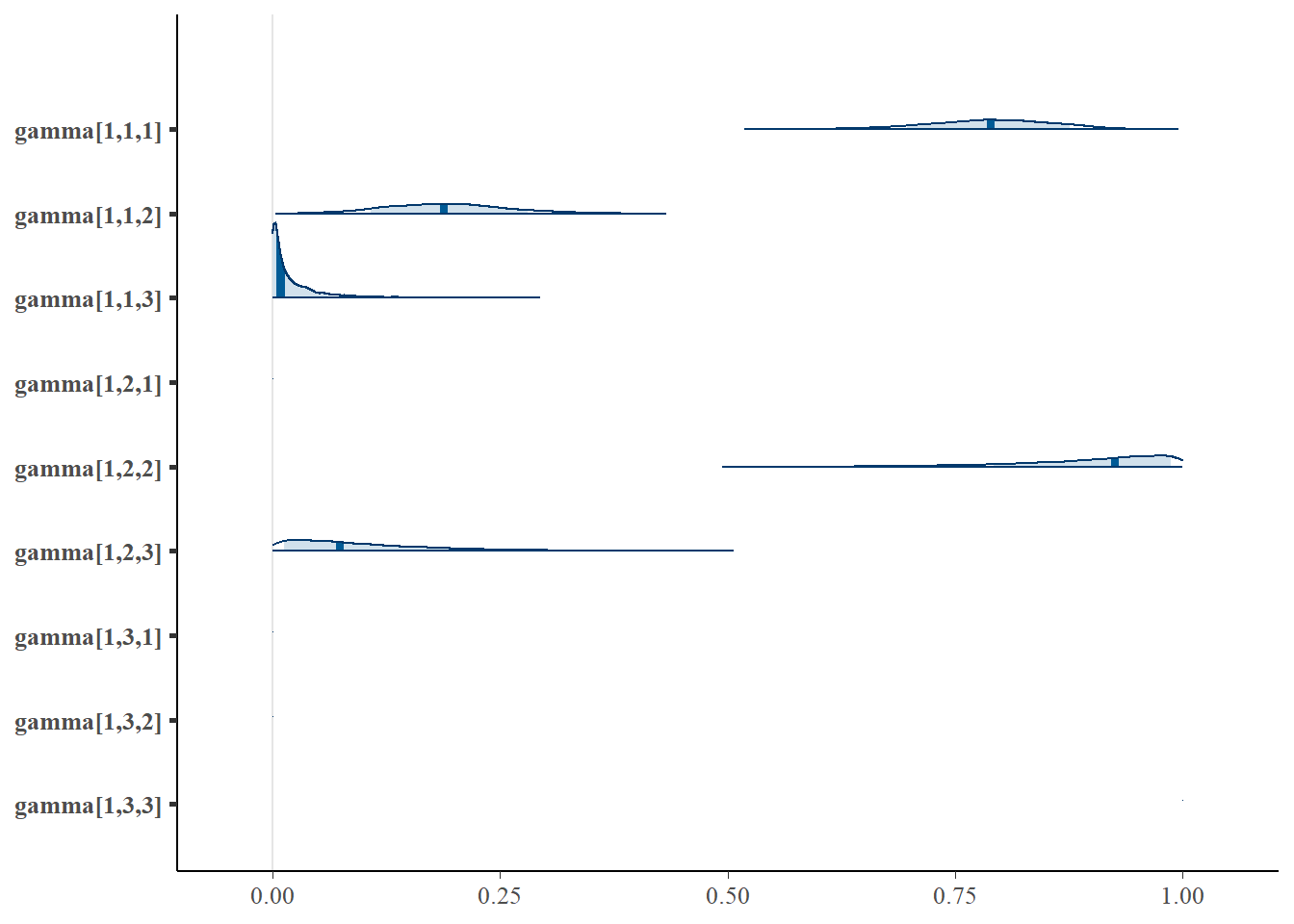
Saving 7 x 5 in imagebayesplot::mcmc_acf(fit.mcmc, pars = use.vars); ggsave("fig/pools_model3_gamma_acf.pdf")Warning: Removed 336 rows containing missing values (geom_segment).Warning: Removed 63 row(s) containing missing values (geom_path).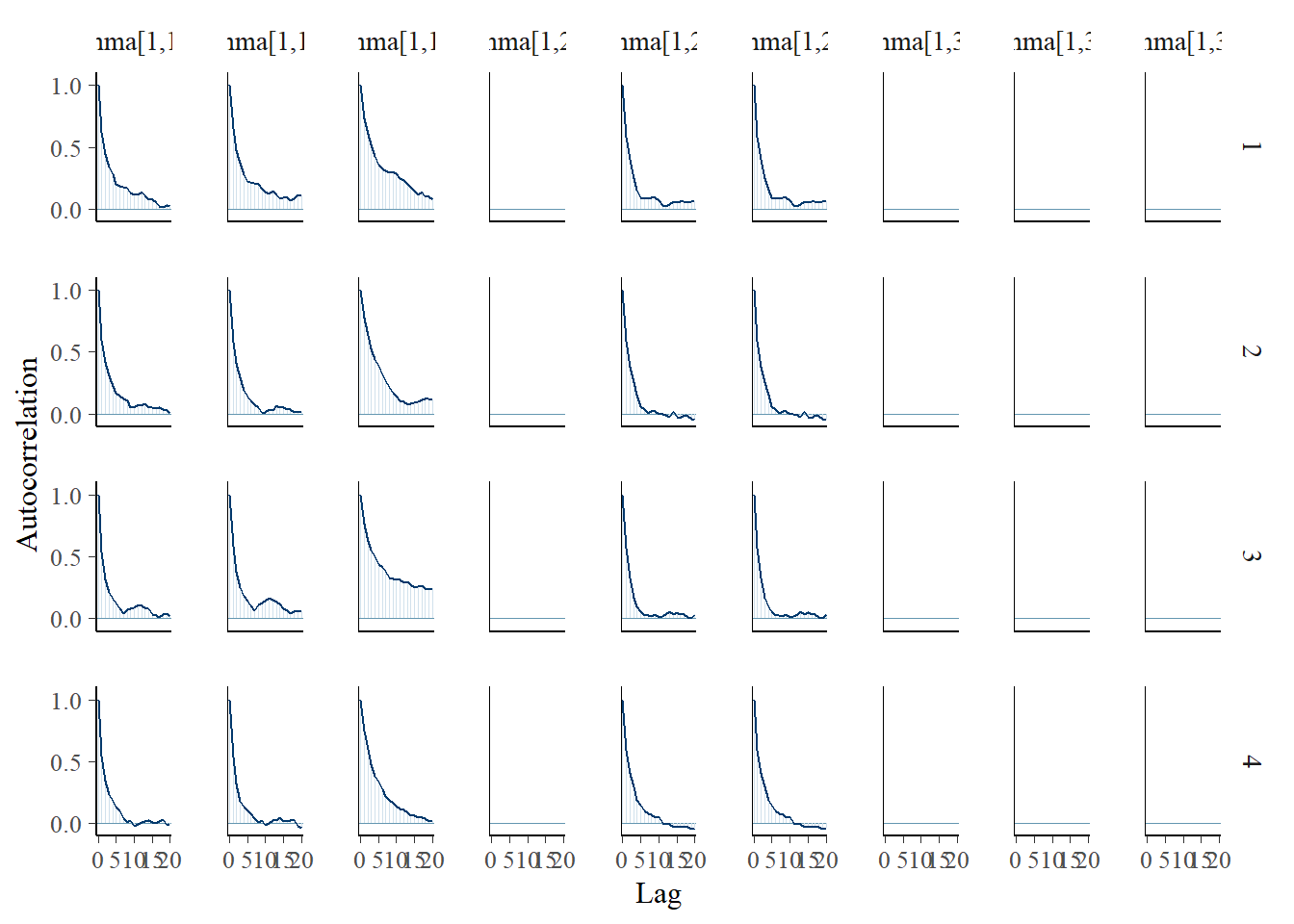
Saving 7 x 5 in imageWarning: Removed 336 rows containing missing values (geom_segment).
Warning: Removed 63 row(s) containing missing values (geom_path).bayesplot::mcmc_trace(fit.mcmc, pars = use.vars); ggsave("fig/pools_model3_gamma_trace.pdf")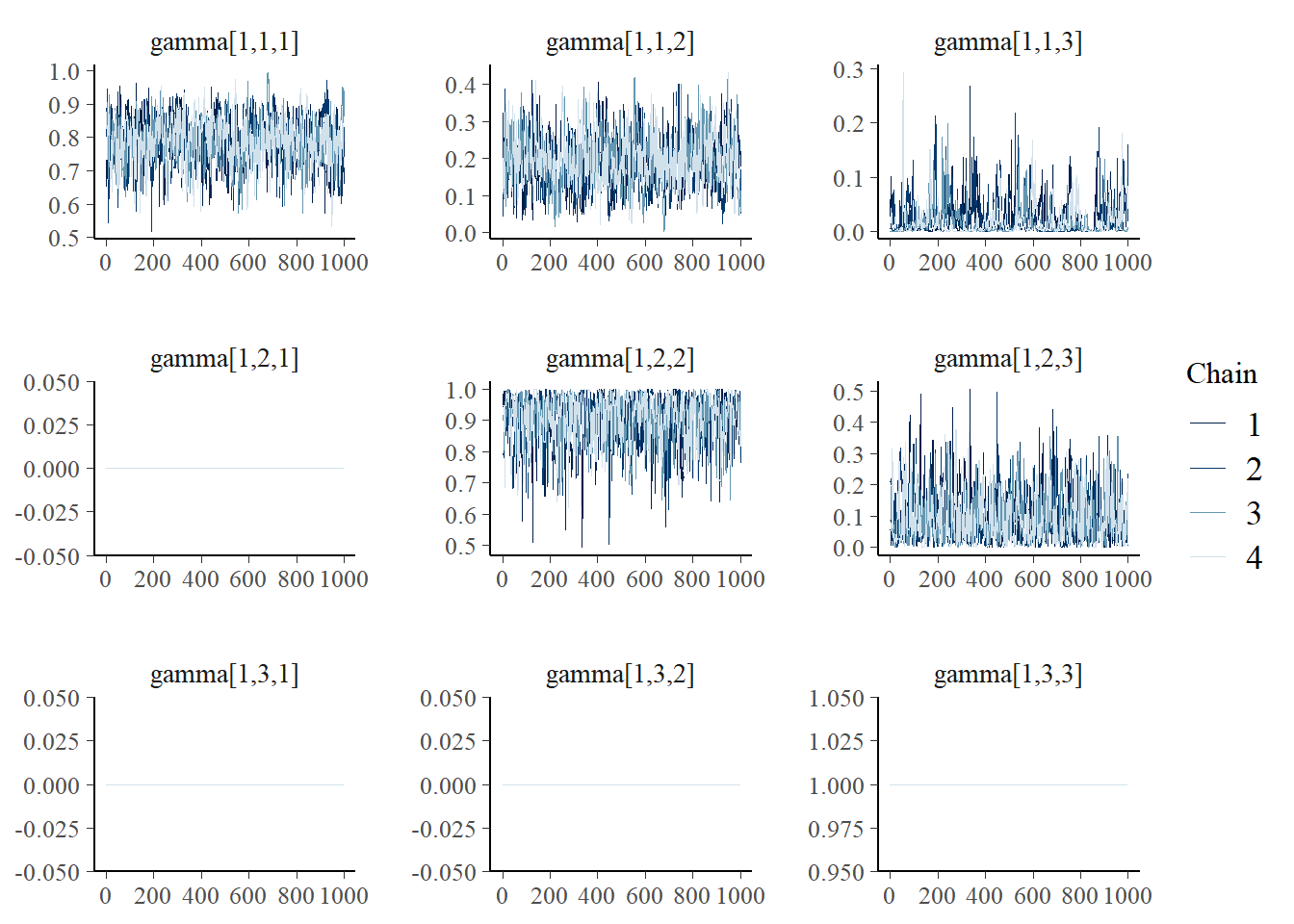
Saving 7 x 5 in imageFactor Reliability Omega (\(\omega\))
bayesplot::mcmc_areas(fit.mcmc, regex_pars = "reli.omega", prob = 0.8); ggsave("fig/pools_model3_omega_dens.pdf")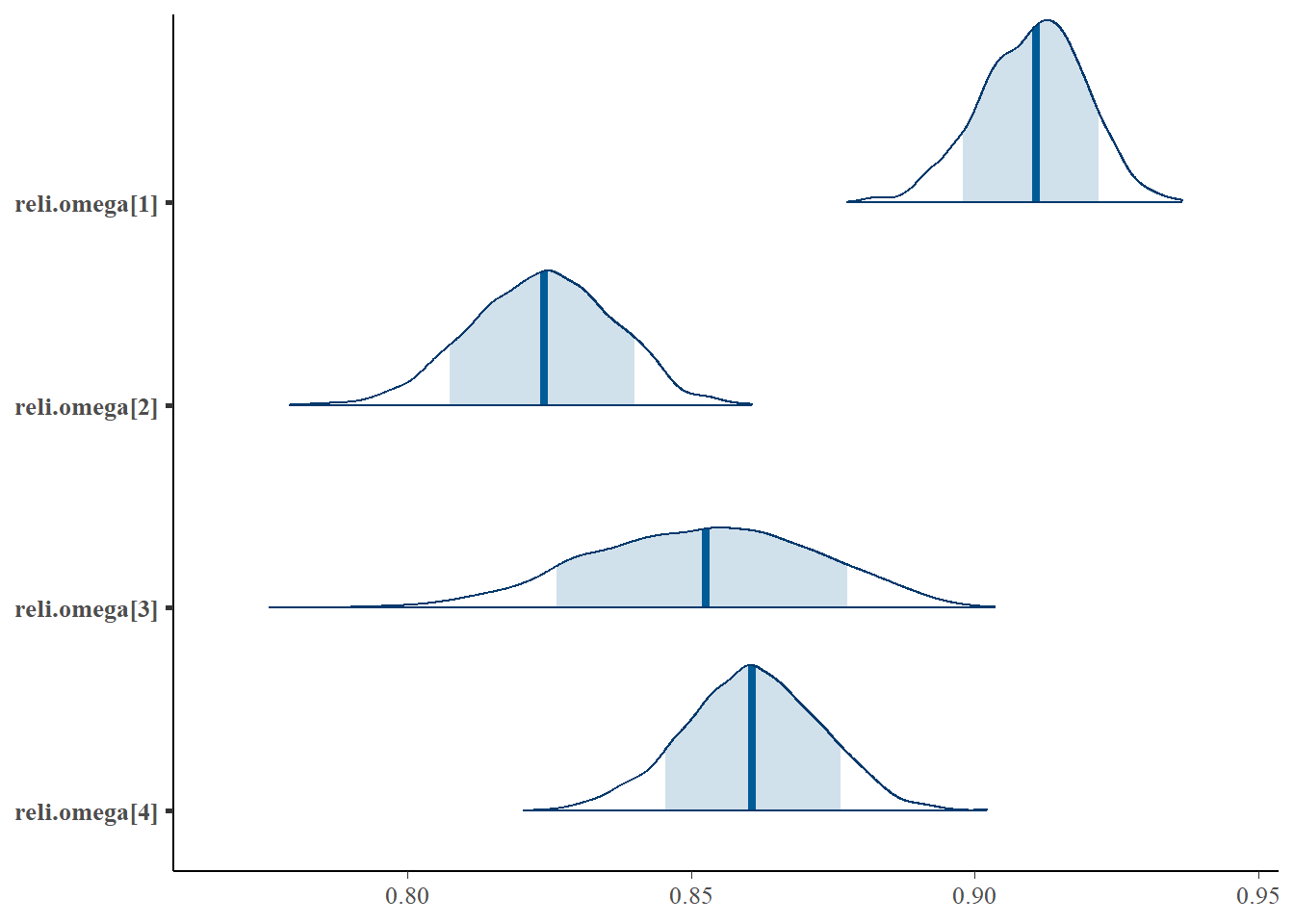
Saving 7 x 5 in imagebayesplot::mcmc_acf(fit.mcmc, regex_pars = "reli.omega"); ggsave("fig/pools_model3_omega_acf.pdf")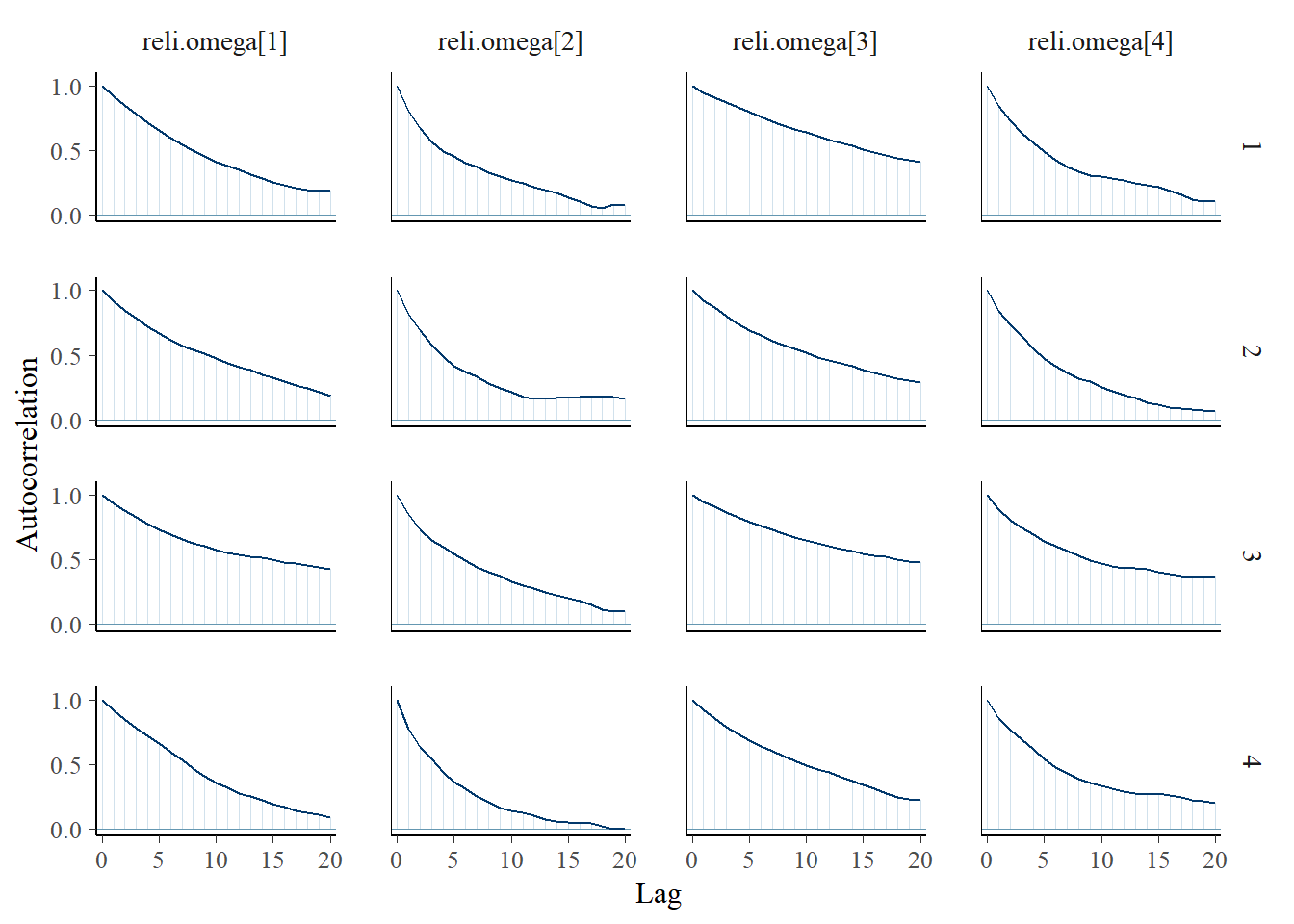
Saving 7 x 5 in imagebayesplot::mcmc_trace(fit.mcmc, regex_pars = "reli.omega"); ggsave("fig/pools_model3_omega_trace.pdf")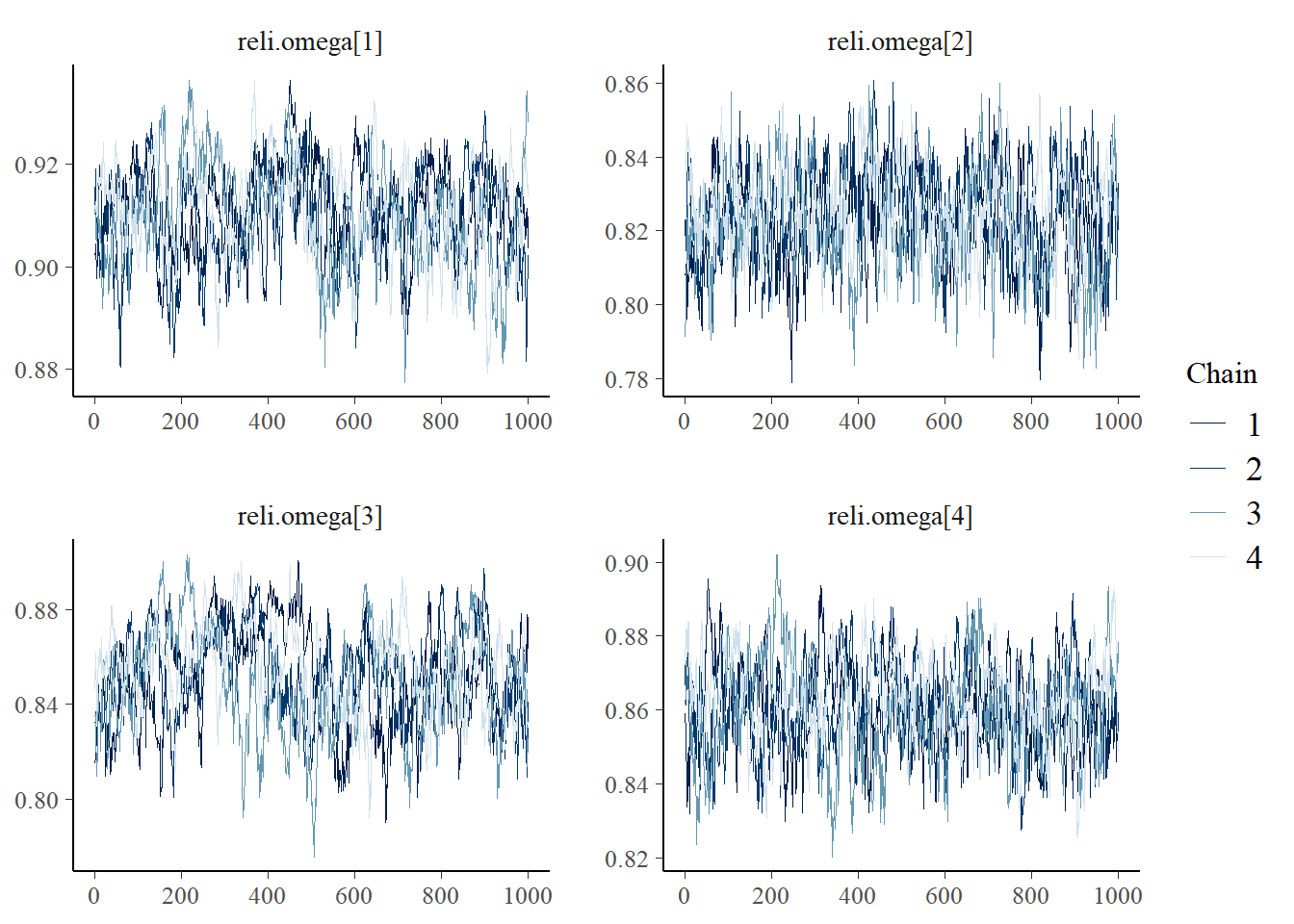
Saving 7 x 5 in imageggmcmc::ggs_grb(fit.mcmc.ggs, family = "reli.omega"); ggsave("fig/pools_model3_omega_grb.pdf")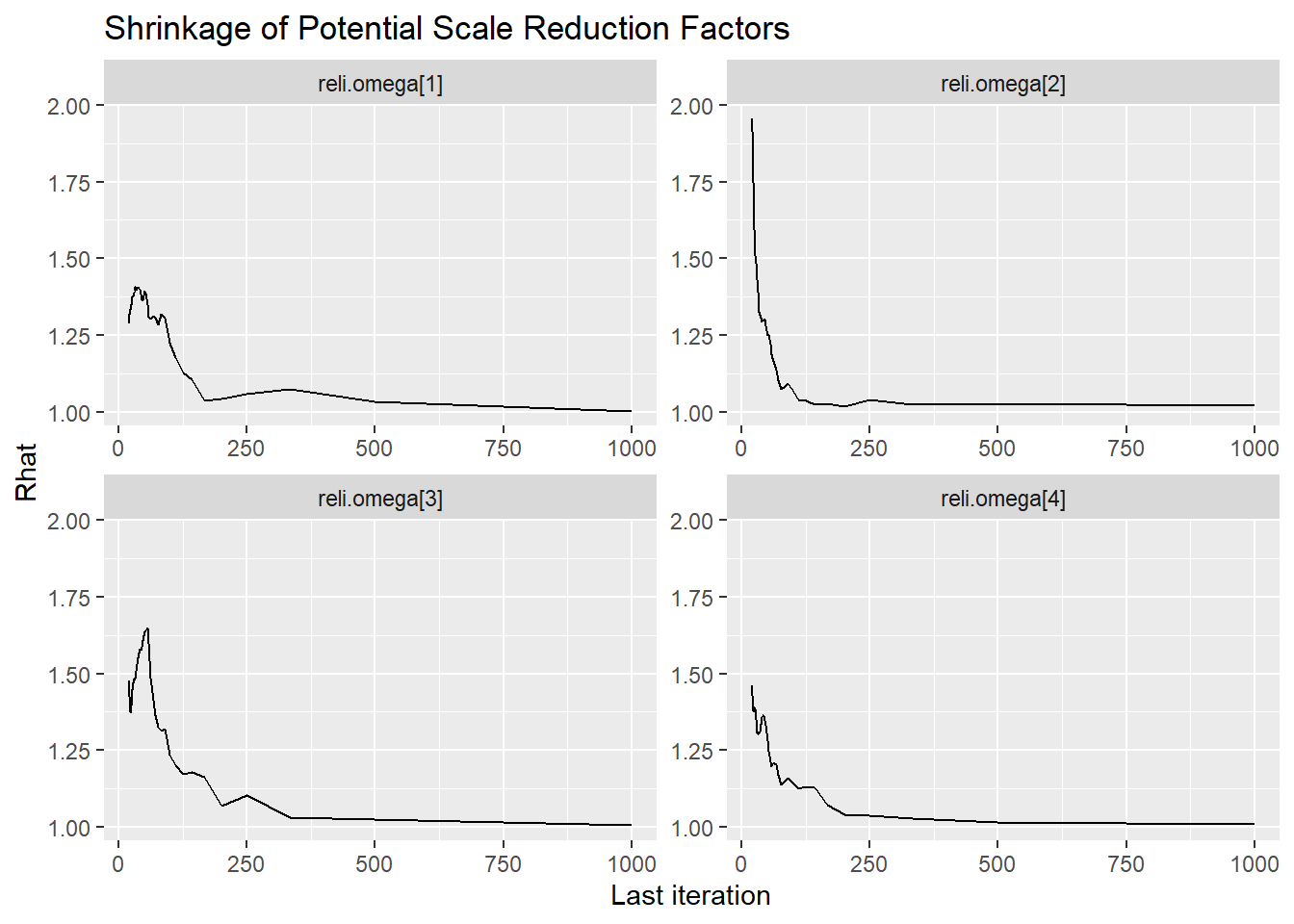
Saving 7 x 5 in image# extract omega posterior for results comparison
extracted_omega <- data.frame(model_3_f1 = fit.mcmc$`reli.omega[1]`,
model_3_f2 = fit.mcmc$`reli.omega[2]`,
model_3_f3 = fit.mcmc$`reli.omega[3]`,
model_3_f4 = fit.mcmc$`reli.omega[4]`)
write.csv(x=extracted_omega, file=paste0(getwd(),"/data/pools/extracted_omega_m3.csv"))Relationship between factor loading and misclassification
keep.var <- c(
paste0('lambda.std[',1:25,']'),
paste0('gamma[',1:25,',1,1]'),
paste0('gamma[',1:25,',2,2]'),
paste0('gamma[',1:25,',3,3]')
)
#plot.dat <- fit.mcmc[,keep.var]
plot.dat <- data.frame(
item = c(paste0("Q4_",c(3:5,9,11,15,18)),
paste0("Q5_",c(1:3,5:6,12)),
paste0("Q6_",c(2,5:8, 11)),
paste0("Q7_",c(2, 4:5, 7:8, 14))),
factor = c(rep('EfL',7), rep('SC',6), rep('IN',6), rep('EnL',6)),
lambda.std = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('lambda.std[',1:25,']'),1],
`gamma[1,1]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',1,1]'),1],
`gamma[2,2]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',2,2]'),1],
`gamma[3,3]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',3,3]'),1],
`gamma[1,2]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',1,2]'),1],
`gamma[2,1]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',2,1]'),1],
`gamma[3,1]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',3,1]'),1],
`gamma[1,3]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',1,3]'),1],
`gamma[2,3]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',2,3]'),1],
`gamma[3,2]` = model.fit$BUGSoutput$summary[rownames(model.fit$BUGSoutput$summary)%in% paste0('gamma[',1:25,',3,2]'),1]
) %>%
pivot_longer(
cols = contains('gamma'),
names_to = 'gamma',
values_to = 'gamma_est'
)
ggplot(plot.dat, aes(x=gamma_est, y=lambda.std, color=factor))+
geom_text(aes(label = item)) +
facet_wrap(.~gamma, ncol=3)+
theme_bw()+
theme(
panel.grid = element_blank()
)
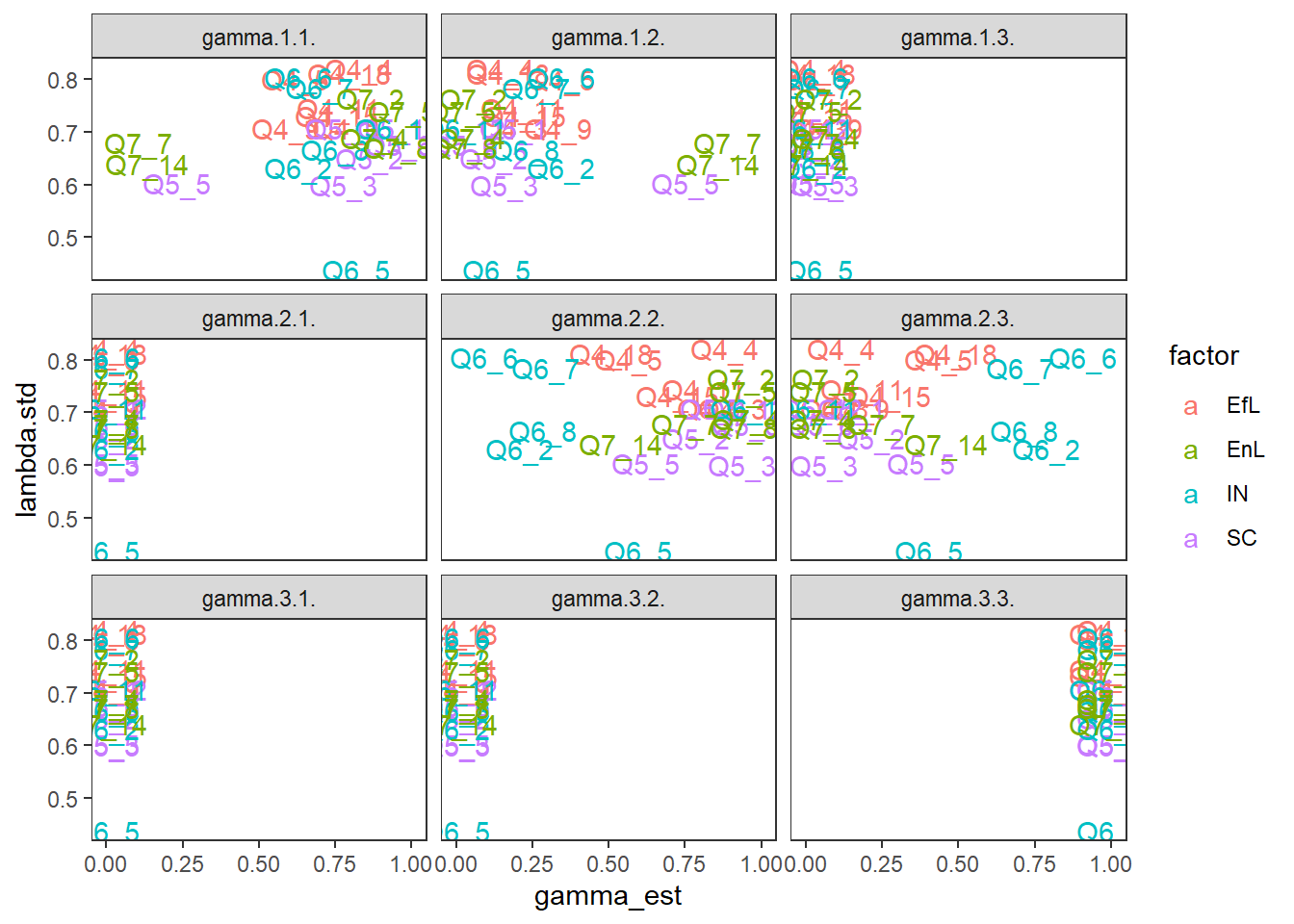# Manuscript Table and Figures
Table
# print to xtable
print(
xtable(
model.fit$BUGSoutput$summary,
caption = c("pools Model 3 posterior distribution summary")
,align = "lrrrrrrrrr"
),
include.rownames=T,
booktabs=T
)% latex table generated in R 4.0.5 by xtable 1.8-4 package
% Wed Feb 02 04:17:43 2022
\begin{table}[ht]
\centering
\begin{tabular}{lrrrrrrrrr}
\toprule
& mean & sd & 2.5\% & 25\% & 50\% & 75\% & 97.5\% & Rhat & n.eff \\
\midrule
deviance & 15491.43 & 122.19 & 15248.15 & 15413.53 & 15490.96 & 15574.98 & 15725.50 & 1.00 & 780.00 \\
gamma[1,1,1] & 0.79 & 0.07 & 0.64 & 0.74 & 0.79 & 0.84 & 0.91 & 1.00 & 4000.00 \\
gamma[2,1,1] & 0.83 & 0.06 & 0.70 & 0.79 & 0.83 & 0.87 & 0.93 & 1.01 & 390.00 \\
gamma[3,1,1] & 0.62 & 0.09 & 0.44 & 0.55 & 0.62 & 0.68 & 0.79 & 1.01 & 410.00 \\
gamma[4,1,1] & 0.59 & 0.10 & 0.40 & 0.52 & 0.59 & 0.65 & 0.78 & 1.01 & 300.00 \\
gamma[5,1,1] & 0.76 & 0.08 & 0.60 & 0.71 & 0.77 & 0.82 & 0.91 & 1.00 & 780.00 \\
gamma[6,1,1] & 0.76 & 0.08 & 0.58 & 0.70 & 0.76 & 0.82 & 0.91 & 1.00 & 910.00 \\
gamma[7,1,1] & 0.80 & 0.07 & 0.65 & 0.75 & 0.80 & 0.85 & 0.92 & 1.01 & 470.00 \\
gamma[8,1,1] & 0.76 & 0.09 & 0.57 & 0.71 & 0.77 & 0.83 & 0.92 & 1.00 & 1400.00 \\
gamma[9,1,1] & 0.86 & 0.12 & 0.57 & 0.82 & 0.89 & 0.95 & 0.99 & 1.01 & 370.00 \\
gamma[10,1,1] & 0.78 & 0.11 & 0.52 & 0.70 & 0.79 & 0.86 & 0.96 & 1.00 & 1000.00 \\
gamma[11,1,1] & 0.23 & 0.06 & 0.12 & 0.19 & 0.23 & 0.27 & 0.36 & 1.00 & 1200.00 \\
gamma[12,1,1] & 0.96 & 0.03 & 0.87 & 0.94 & 0.96 & 0.98 & 1.00 & 1.00 & 1500.00 \\
gamma[13,1,1] & 0.96 & 0.03 & 0.89 & 0.95 & 0.97 & 0.98 & 1.00 & 1.00 & 3200.00 \\
gamma[14,1,1] & 0.63 & 0.13 & 0.38 & 0.54 & 0.62 & 0.72 & 0.87 & 1.00 & 790.00 \\
gamma[15,1,1] & 0.82 & 0.11 & 0.58 & 0.75 & 0.84 & 0.91 & 0.98 & 1.01 & 300.00 \\
gamma[16,1,1] & 0.63 & 0.11 & 0.39 & 0.55 & 0.63 & 0.71 & 0.84 & 1.01 & 340.00 \\
gamma[17,1,1] & 0.70 & 0.10 & 0.48 & 0.63 & 0.70 & 0.77 & 0.89 & 1.01 & 250.00 \\
gamma[18,1,1] & 0.75 & 0.11 & 0.53 & 0.68 & 0.76 & 0.83 & 0.94 & 1.01 & 230.00 \\
gamma[19,1,1] & 0.95 & 0.03 & 0.87 & 0.94 & 0.96 & 0.98 & 0.99 & 1.00 & 1300.00 \\
gamma[20,1,1] & 0.87 & 0.06 & 0.73 & 0.83 & 0.87 & 0.91 & 0.96 & 1.01 & 450.00 \\
gamma[21,1,1] & 0.88 & 0.06 & 0.74 & 0.84 & 0.89 & 0.93 & 0.98 & 1.00 & 700.00 \\
gamma[22,1,1] & 0.97 & 0.02 & 0.91 & 0.96 & 0.98 & 0.99 & 1.00 & 1.01 & 760.00 \\
gamma[23,1,1] & 0.11 & 0.04 & 0.04 & 0.08 & 0.10 & 0.13 & 0.19 & 1.00 & 4000.00 \\
gamma[24,1,1] & 0.96 & 0.03 & 0.87 & 0.94 & 0.96 & 0.98 & 1.00 & 1.01 & 560.00 \\
gamma[25,1,1] & 0.13 & 0.04 & 0.07 & 0.11 & 0.13 & 0.16 & 0.21 & 1.01 & 460.00 \\
gamma[1,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[2,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[3,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[4,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[5,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[6,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[7,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[8,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[9,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[10,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[11,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[12,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[13,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[14,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[15,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[16,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[17,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[18,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[19,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[20,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[21,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[22,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[23,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[24,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[25,2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[1,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[2,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[3,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[4,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[5,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[6,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[7,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[8,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[9,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[10,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[11,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[12,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[13,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[14,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[15,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[16,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[17,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[18,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[19,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[20,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[21,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[22,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[23,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[24,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[25,3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[1,1,2] & 0.19 & 0.07 & 0.07 & 0.14 & 0.19 & 0.23 & 0.33 & 1.01 & 1100.00 \\
gamma[2,1,2] & 0.15 & 0.05 & 0.05 & 0.11 & 0.14 & 0.18 & 0.27 & 1.00 & 4000.00 \\
gamma[3,1,2] & 0.35 & 0.09 & 0.18 & 0.28 & 0.34 & 0.41 & 0.54 & 1.01 & 280.00 \\
gamma[4,1,2] & 0.34 & 0.11 & 0.12 & 0.26 & 0.34 & 0.41 & 0.54 & 1.01 & 750.00 \\
gamma[5,1,2] & 0.22 & 0.08 & 0.06 & 0.16 & 0.21 & 0.27 & 0.38 & 1.01 & 1800.00 \\
gamma[6,1,2] & 0.23 & 0.09 & 0.07 & 0.16 & 0.22 & 0.28 & 0.40 & 1.01 & 430.00 \\
gamma[7,1,2] & 0.17 & 0.07 & 0.05 & 0.13 & 0.17 & 0.21 & 0.32 & 1.08 & 88.00 \\
gamma[8,1,2] & 0.19 & 0.10 & 0.01 & 0.12 & 0.18 & 0.25 & 0.39 & 1.11 & 91.00 \\
gamma[9,1,2] & 0.12 & 0.11 & 0.00 & 0.04 & 0.09 & 0.17 & 0.41 & 1.02 & 350.00 \\
gamma[10,1,2] & 0.16 & 0.11 & 0.01 & 0.07 & 0.14 & 0.23 & 0.43 & 1.02 & 270.00 \\
gamma[11,1,2] & 0.75 & 0.06 & 0.63 & 0.71 & 0.75 & 0.79 & 0.86 & 1.00 & 4000.00 \\
gamma[12,1,2] & 0.03 & 0.03 & 0.00 & 0.01 & 0.02 & 0.04 & 0.10 & 1.01 & 450.00 \\
gamma[13,1,2] & 0.03 & 0.03 & 0.00 & 0.01 & 0.02 & 0.04 & 0.10 & 1.00 & 3100.00 \\
gamma[14,1,2] & 0.35 & 0.12 & 0.10 & 0.26 & 0.35 & 0.43 & 0.59 & 1.00 & 610.00 \\
gamma[15,1,2] & 0.13 & 0.10 & 0.00 & 0.05 & 0.11 & 0.20 & 0.38 & 1.01 & 400.00 \\
gamma[16,1,2] & 0.35 & 0.11 & 0.15 & 0.27 & 0.34 & 0.42 & 0.58 & 1.00 & 830.00 \\
gamma[17,1,2] & 0.26 & 0.10 & 0.09 & 0.19 & 0.26 & 0.33 & 0.47 & 1.01 & 330.00 \\
gamma[18,1,2] & 0.23 & 0.10 & 0.05 & 0.15 & 0.22 & 0.30 & 0.45 & 1.03 & 140.00 \\
gamma[19,1,2] & 0.03 & 0.03 & 0.00 & 0.01 & 0.02 & 0.04 & 0.10 & 1.01 & 590.00 \\
gamma[20,1,2] & 0.06 & 0.04 & 0.00 & 0.02 & 0.05 & 0.08 & 0.16 & 1.01 & 550.00 \\
gamma[21,1,2] & 0.05 & 0.05 & 0.00 & 0.02 & 0.04 & 0.07 & 0.18 & 1.01 & 4000.00 \\
gamma[22,1,2] & 0.02 & 0.02 & 0.00 & 0.01 & 0.01 & 0.03 & 0.07 & 1.00 & 2300.00 \\
gamma[23,1,2] & 0.89 & 0.04 & 0.80 & 0.87 & 0.89 & 0.92 & 0.96 & 1.00 & 1900.00 \\
gamma[24,1,2] & 0.03 & 0.02 & 0.00 & 0.01 & 0.02 & 0.04 & 0.09 & 1.00 & 1100.00 \\
gamma[25,1,2] & 0.86 & 0.04 & 0.78 & 0.84 & 0.86 & 0.89 & 0.93 & 1.00 & 560.00 \\
gamma[1,2,2] & 0.91 & 0.08 & 0.71 & 0.86 & 0.93 & 0.97 & 1.00 & 1.00 & 1400.00 \\
gamma[2,2,2] & 0.88 & 0.08 & 0.70 & 0.84 & 0.90 & 0.94 & 0.99 & 1.00 & 2300.00 \\
gamma[3,2,2] & 0.56 & 0.10 & 0.37 & 0.49 & 0.56 & 0.63 & 0.78 & 1.00 & 740.00 \\
gamma[4,2,2] & 0.84 & 0.11 & 0.58 & 0.77 & 0.85 & 0.92 & 0.99 & 1.01 & 540.00 \\
gamma[5,2,2] & 0.81 & 0.11 & 0.57 & 0.74 & 0.82 & 0.90 & 0.99 & 1.00 & 1700.00 \\
gamma[6,2,2] & 0.73 & 0.12 & 0.50 & 0.64 & 0.72 & 0.82 & 0.96 & 1.01 & 460.00 \\
gamma[7,2,2] & 0.51 & 0.11 & 0.30 & 0.43 & 0.50 & 0.58 & 0.74 & 1.02 & 140.00 \\
gamma[8,2,2] & 0.85 & 0.09 & 0.64 & 0.79 & 0.86 & 0.92 & 0.99 & 1.00 & 1000.00 \\
gamma[9,2,2] & 0.79 & 0.10 & 0.57 & 0.73 & 0.79 & 0.86 & 0.96 & 1.00 & 3400.00 \\
gamma[10,2,2] & 0.94 & 0.05 & 0.81 & 0.91 & 0.95 & 0.98 & 1.00 & 1.01 & 740.00 \\
gamma[11,2,2] & 0.62 & 0.05 & 0.52 & 0.59 & 0.62 & 0.66 & 0.73 & 1.00 & 3100.00 \\
gamma[12,2,2] & 0.95 & 0.04 & 0.85 & 0.93 & 0.96 & 0.98 & 1.00 & 1.00 & 4000.00 \\
gamma[13,2,2] & 0.95 & 0.04 & 0.84 & 0.93 & 0.96 & 0.98 & 1.00 & 1.00 & 4000.00 \\
gamma[14,2,2] & 0.21 & 0.05 & 0.13 & 0.18 & 0.21 & 0.24 & 0.31 & 1.00 & 1200.00 \\
gamma[15,2,2] & 0.60 & 0.15 & 0.32 & 0.49 & 0.59 & 0.70 & 0.91 & 1.00 & 770.00 \\
gamma[16,2,2] & 0.09 & 0.03 & 0.05 & 0.07 & 0.09 & 0.11 & 0.15 & 1.00 & 1300.00 \\
gamma[17,2,2] & 0.30 & 0.07 & 0.17 & 0.25 & 0.29 & 0.34 & 0.44 & 1.00 & 590.00 \\
gamma[18,2,2] & 0.28 & 0.06 & 0.17 & 0.24 & 0.28 & 0.33 & 0.42 & 1.01 & 290.00 \\
gamma[19,2,2] & 0.97 & 0.03 & 0.89 & 0.96 & 0.98 & 0.99 & 1.00 & 1.00 & 1100.00 \\
gamma[20,2,2] & 0.93 & 0.05 & 0.80 & 0.91 & 0.95 & 0.97 & 1.00 & 1.02 & 220.00 \\
gamma[21,2,2] & 0.95 & 0.04 & 0.84 & 0.94 & 0.97 & 0.98 & 1.00 & 1.00 & 4000.00 \\
gamma[22,2,2] & 0.94 & 0.04 & 0.83 & 0.92 & 0.95 & 0.98 & 1.00 & 1.00 & 1100.00 \\
gamma[23,2,2] & 0.75 & 0.06 & 0.63 & 0.70 & 0.75 & 0.79 & 0.88 & 1.00 & 2300.00 \\
gamma[24,2,2] & 0.94 & 0.05 & 0.81 & 0.92 & 0.96 & 0.98 & 1.00 & 1.00 & 4000.00 \\
gamma[25,2,2] & 0.54 & 0.05 & 0.44 & 0.50 & 0.54 & 0.58 & 0.64 & 1.00 & 2200.00 \\
gamma[1,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[2,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[3,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[4,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[5,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[6,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[7,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[8,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[9,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[10,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[11,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[12,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[13,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[14,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[15,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[16,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[17,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[18,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[19,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[20,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[21,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[22,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[23,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[24,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[25,3,2] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
gamma[1,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.11 & 1.01 & 330.00 \\
gamma[2,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.10 & 1.03 & 170.00 \\
gamma[3,1,3] & 0.03 & 0.05 & 0.00 & 0.00 & 0.02 & 0.05 & 0.17 & 1.02 & 280.00 \\
gamma[4,1,3] & 0.08 & 0.06 & 0.00 & 0.02 & 0.06 & 0.11 & 0.23 & 1.03 & 140.00 \\
gamma[5,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.10 & 1.09 & 56.00 \\
gamma[6,1,3] & 0.02 & 0.02 & 0.00 & 0.00 & 0.01 & 0.03 & 0.08 & 1.01 & 200.00 \\
gamma[7,1,3] & 0.03 & 0.03 & 0.00 & 0.00 & 0.02 & 0.04 & 0.13 & 1.06 & 57.00 \\
gamma[8,1,3] & 0.05 & 0.05 & 0.00 & 0.01 & 0.03 & 0.07 & 0.19 & 1.11 & 45.00 \\
gamma[9,1,3] & 0.02 & 0.02 & 0.00 & 0.00 & 0.01 & 0.02 & 0.07 & 1.01 & 460.00 \\
gamma[10,1,3] & 0.06 & 0.06 & 0.00 & 0.02 & 0.05 & 0.10 & 0.22 & 1.02 & 170.00 \\
gamma[11,1,3] & 0.02 & 0.02 & 0.00 & 0.00 & 0.01 & 0.02 & 0.06 & 1.05 & 110.00 \\
gamma[12,1,3] & 0.02 & 0.02 & 0.00 & 0.00 & 0.01 & 0.02 & 0.08 & 1.00 & 1300.00 \\
gamma[13,1,3] & 0.01 & 0.02 & 0.00 & 0.00 & 0.01 & 0.01 & 0.05 & 1.03 & 150.00 \\
gamma[14,1,3] & 0.03 & 0.03 & 0.00 & 0.00 & 0.01 & 0.04 & 0.12 & 1.02 & 240.00 \\
gamma[15,1,3] & 0.04 & 0.05 & 0.00 & 0.01 & 0.02 & 0.06 & 0.21 & 1.01 & 390.00 \\
gamma[16,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.12 & 1.03 & 110.00 \\
gamma[17,1,3] & 0.04 & 0.04 & 0.00 & 0.01 & 0.02 & 0.05 & 0.16 & 1.03 & 180.00 \\
gamma[18,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.10 & 1.11 & 63.00 \\
gamma[19,1,3] & 0.02 & 0.02 & 0.00 & 0.00 & 0.01 & 0.03 & 0.08 & 1.03 & 150.00 \\
gamma[20,1,3] & 0.08 & 0.06 & 0.00 & 0.03 & 0.06 & 0.11 & 0.21 & 1.01 & 540.00 \\
gamma[21,1,3] & 0.07 & 0.05 & 0.00 & 0.03 & 0.06 & 0.10 & 0.19 & 1.02 & 520.00 \\
gamma[22,1,3] & 0.01 & 0.01 & 0.00 & 0.00 & 0.00 & 0.01 & 0.05 & 1.12 & 63.00 \\
gamma[23,1,3] & 0.00 & 0.01 & 0.00 & 0.00 & 0.00 & 0.01 & 0.02 & 1.06 & 340.00 \\
gamma[24,1,3] & 0.02 & 0.03 & 0.00 & 0.00 & 0.01 & 0.03 & 0.10 & 1.01 & 280.00 \\
gamma[25,1,3] & 0.01 & 0.01 & 0.00 & 0.00 & 0.00 & 0.01 & 0.03 & 1.02 & 250.00 \\
gamma[1,2,3] & 0.09 & 0.08 & 0.00 & 0.03 & 0.07 & 0.14 & 0.29 & 1.01 & 1600.00 \\
gamma[2,2,3] & 0.12 & 0.08 & 0.01 & 0.06 & 0.10 & 0.16 & 0.30 & 1.00 & 4000.00 \\
gamma[3,2,3] & 0.44 & 0.10 & 0.22 & 0.37 & 0.44 & 0.51 & 0.63 & 1.01 & 750.00 \\
gamma[4,2,3] & 0.16 & 0.11 & 0.01 & 0.08 & 0.15 & 0.23 & 0.42 & 1.01 & 550.00 \\
gamma[5,2,3] & 0.19 & 0.11 & 0.01 & 0.10 & 0.18 & 0.26 & 0.43 & 1.01 & 970.00 \\
gamma[6,2,3] & 0.27 & 0.12 & 0.04 & 0.18 & 0.28 & 0.36 & 0.50 & 1.01 & 430.00 \\
gamma[7,2,3] & 0.49 & 0.11 & 0.26 & 0.42 & 0.50 & 0.57 & 0.70 & 1.01 & 220.00 \\
gamma[8,2,3] & 0.15 & 0.09 & 0.01 & 0.08 & 0.14 & 0.21 & 0.36 & 1.00 & 1100.00 \\
gamma[9,2,3] & 0.21 & 0.10 & 0.04 & 0.14 & 0.21 & 0.27 & 0.43 & 1.01 & 1200.00 \\
gamma[10,2,3] & 0.06 & 0.05 & 0.00 & 0.02 & 0.05 & 0.09 & 0.19 & 1.00 & 830.00 \\
gamma[11,2,3] & 0.38 & 0.05 & 0.27 & 0.34 & 0.38 & 0.41 & 0.48 & 1.00 & 3300.00 \\
gamma[12,2,3] & 0.05 & 0.04 & 0.00 & 0.02 & 0.04 & 0.07 & 0.15 & 1.01 & 910.00 \\
gamma[13,2,3] & 0.05 & 0.04 & 0.00 & 0.02 & 0.04 & 0.07 & 0.16 & 1.00 & 4000.00 \\
gamma[14,2,3] & 0.79 & 0.05 & 0.69 & 0.76 & 0.79 & 0.82 & 0.87 & 1.00 & 1100.00 \\
gamma[15,2,3] & 0.40 & 0.15 & 0.09 & 0.30 & 0.41 & 0.51 & 0.68 & 1.01 & 770.00 \\
gamma[16,2,3] & 0.91 & 0.03 & 0.85 & 0.89 & 0.91 & 0.93 & 0.95 & 1.00 & 1500.00 \\
gamma[17,2,3] & 0.70 & 0.07 & 0.56 & 0.66 & 0.71 & 0.75 & 0.83 & 1.00 & 640.00 \\
gamma[18,2,3] & 0.72 & 0.06 & 0.58 & 0.67 & 0.72 & 0.76 & 0.83 & 1.01 & 310.00 \\
gamma[19,2,3] & 0.03 & 0.03 & 0.00 & 0.01 & 0.02 & 0.04 & 0.11 & 1.00 & 940.00 \\
gamma[20,2,3] & 0.07 & 0.05 & 0.00 & 0.03 & 0.05 & 0.09 & 0.20 & 1.01 & 390.00 \\
gamma[21,2,3] & 0.05 & 0.04 & 0.00 & 0.02 & 0.03 & 0.06 & 0.16 & 1.00 & 2700.00 \\
gamma[22,2,3] & 0.06 & 0.04 & 0.00 & 0.02 & 0.05 & 0.08 & 0.17 & 1.01 & 370.00 \\
gamma[23,2,3] & 0.25 & 0.06 & 0.12 & 0.21 & 0.25 & 0.30 & 0.37 & 1.00 & 4000.00 \\
gamma[24,2,3] & 0.06 & 0.05 & 0.00 & 0.02 & 0.04 & 0.08 & 0.19 & 1.00 & 2800.00 \\
gamma[25,2,3] & 0.46 & 0.05 & 0.36 & 0.42 & 0.46 & 0.50 & 0.56 & 1.00 & 1900.00 \\
gamma[1,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[2,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[3,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[4,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[5,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[6,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[7,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[8,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[9,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[10,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[11,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[12,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[13,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[14,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[15,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[16,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[17,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[18,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[19,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[20,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[21,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[22,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[23,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[24,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
gamma[25,3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
inv.phi[1,1] & 3.20 & 1.55 & 0.90 & 2.04 & 2.96 & 4.08 & 6.88 & 1.03 & 110.00 \\
inv.phi[2,1] & -0.52 & 1.06 & -2.78 & -1.17 & -0.50 & 0.17 & 1.57 & 1.05 & 53.00 \\
inv.phi[3,1] & -1.17 & 1.12 & -3.74 & -1.79 & -1.04 & -0.42 & 0.72 & 1.06 & 54.00 \\
inv.phi[4,1] & -1.19 & 1.35 & -4.24 & -1.97 & -1.04 & -0.24 & 0.99 & 1.04 & 68.00 \\
inv.phi[1,2] & -0.52 & 1.06 & -2.78 & -1.17 & -0.50 & 0.17 & 1.57 & 1.05 & 53.00 \\
inv.phi[2,2] & 2.93 & 1.51 & 0.68 & 1.83 & 2.64 & 3.79 & 6.54 & 1.10 & 34.00 \\
inv.phi[3,2] & -0.10 & 0.95 & -2.18 & -0.63 & -0.06 & 0.50 & 1.65 & 1.03 & 82.00 \\
inv.phi[4,2] & -2.00 & 1.42 & -5.26 & -2.81 & -1.75 & -0.93 & 0.07 & 1.05 & 62.00 \\
inv.phi[1,3] & -1.17 & 1.12 & -3.74 & -1.79 & -1.04 & -0.42 & 0.72 & 1.06 & 54.00 \\
inv.phi[2,3] & -0.10 & 0.95 & -2.18 & -0.63 & -0.06 & 0.50 & 1.65 & 1.03 & 82.00 \\
inv.phi[3,3] & 2.60 & 1.32 & 0.70 & 1.60 & 2.39 & 3.32 & 5.71 & 1.05 & 59.00 \\
inv.phi[4,3] & -0.82 & 1.27 & -3.62 & -1.60 & -0.69 & 0.10 & 1.34 & 1.05 & 65.00 \\
inv.phi[1,4] & -1.19 & 1.35 & -4.24 & -1.97 & -1.04 & -0.24 & 0.99 & 1.04 & 68.00 \\
inv.phi[2,4] & -2.00 & 1.42 & -5.26 & -2.81 & -1.75 & -0.93 & 0.07 & 1.05 & 62.00 \\
inv.phi[3,4] & -0.82 & 1.27 & -3.62 & -1.60 & -0.69 & 0.10 & 1.34 & 1.05 & 65.00 \\
inv.phi[4,4] & 3.89 & 2.18 & 0.77 & 2.24 & 3.50 & 5.15 & 9.04 & 1.03 & 95.00 \\
lambda[1] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[2] & 1.46 & 0.18 & 1.13 & 1.33 & 1.45 & 1.58 & 1.84 & 1.01 & 620.00 \\
lambda[3] & 1.36 & 0.18 & 1.05 & 1.23 & 1.34 & 1.47 & 1.73 & 1.01 & 460.00 \\
lambda[4] & 1.01 & 0.13 & 0.76 & 0.93 & 1.01 & 1.10 & 1.29 & 1.02 & 100.00 \\
lambda[5] & 1.13 & 0.13 & 0.90 & 1.04 & 1.12 & 1.21 & 1.38 & 1.01 & 500.00 \\
lambda[6] & 1.09 & 0.14 & 0.83 & 0.99 & 1.08 & 1.18 & 1.36 & 1.01 & 240.00 \\
lambda[7] & 1.41 & 0.18 & 1.10 & 1.28 & 1.40 & 1.54 & 1.80 & 1.01 & 330.00 \\
lambda[8] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[9] & 0.86 & 0.09 & 0.69 & 0.80 & 0.86 & 0.93 & 1.05 & 1.02 & 140.00 \\
lambda[10] & 0.76 & 0.10 & 0.58 & 0.69 & 0.75 & 0.82 & 0.96 & 1.01 & 230.00 \\
lambda[11] & 0.76 & 0.10 & 0.58 & 0.69 & 0.76 & 0.83 & 0.97 & 1.01 & 290.00 \\
lambda[12] & 0.92 & 0.09 & 0.77 & 0.86 & 0.92 & 0.98 & 1.11 & 1.01 & 290.00 \\
lambda[13] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[14] & 0.83 & 0.13 & 0.58 & 0.74 & 0.82 & 0.92 & 1.09 & 1.03 & 110.00 \\
lambda[15] & 0.49 & 0.07 & 0.36 & 0.44 & 0.48 & 0.54 & 0.65 & 1.02 & 180.00 \\
lambda[16] & 1.40 & 0.25 & 0.96 & 1.23 & 1.38 & 1.56 & 1.92 & 1.02 & 120.00 \\
lambda[17] & 1.29 & 0.21 & 0.93 & 1.14 & 1.28 & 1.45 & 1.70 & 1.04 & 71.00 \\
lambda[18] & 0.91 & 0.14 & 0.66 & 0.81 & 0.90 & 0.99 & 1.21 & 1.02 & 160.00 \\
lambda[19] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
lambda[20] & 1.20 & 0.13 & 0.97 & 1.11 & 1.19 & 1.28 & 1.47 & 1.01 & 760.00 \\
lambda[21] & 0.96 & 0.10 & 0.77 & 0.88 & 0.95 & 1.02 & 1.16 & 1.00 & 870.00 \\
lambda[22] & 1.11 & 0.10 & 0.92 & 1.04 & 1.11 & 1.18 & 1.32 & 1.01 & 240.00 \\
lambda[23] & 0.93 & 0.11 & 0.73 & 0.86 & 0.93 & 1.01 & 1.18 & 1.01 & 270.00 \\
lambda[24] & 0.91 & 0.09 & 0.75 & 0.85 & 0.90 & 0.97 & 1.11 & 1.01 & 430.00 \\
lambda[25] & 0.84 & 0.10 & 0.66 & 0.77 & 0.84 & 0.90 & 1.05 & 1.01 & 250.00 \\
lambda.std[1] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[2] & 0.82 & 0.03 & 0.75 & 0.80 & 0.82 & 0.84 & 0.88 & 1.01 & 840.00 \\
lambda.std[3] & 0.80 & 0.04 & 0.72 & 0.78 & 0.80 & 0.83 & 0.87 & 1.01 & 390.00 \\
lambda.std[4] & 0.71 & 0.05 & 0.61 & 0.68 & 0.71 & 0.74 & 0.79 & 1.02 & 110.00 \\
lambda.std[5] & 0.74 & 0.04 & 0.67 & 0.72 & 0.75 & 0.77 & 0.81 & 1.01 & 420.00 \\
lambda.std[6] & 0.73 & 0.04 & 0.64 & 0.70 & 0.73 & 0.76 & 0.81 & 1.01 & 270.00 \\
lambda.std[7] & 0.81 & 0.04 & 0.74 & 0.79 & 0.81 & 0.84 & 0.87 & 1.01 & 290.00 \\
lambda.std[8] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[9] & 0.65 & 0.04 & 0.57 & 0.62 & 0.65 & 0.68 & 0.72 & 1.02 & 140.00 \\
lambda.std[10] & 0.60 & 0.05 & 0.50 & 0.57 & 0.60 & 0.63 & 0.69 & 1.02 & 210.00 \\
lambda.std[11] & 0.60 & 0.05 & 0.50 & 0.57 & 0.60 & 0.64 & 0.70 & 1.01 & 290.00 \\
lambda.std[12] & 0.68 & 0.03 & 0.61 & 0.65 & 0.68 & 0.70 & 0.74 & 1.01 & 290.00 \\
lambda.std[13] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[14] & 0.63 & 0.06 & 0.50 & 0.59 & 0.64 & 0.68 & 0.74 & 1.03 & 110.00 \\
lambda.std[15] & 0.44 & 0.05 & 0.34 & 0.40 & 0.44 & 0.47 & 0.54 & 1.02 & 180.00 \\
lambda.std[16] & 0.80 & 0.05 & 0.69 & 0.78 & 0.81 & 0.84 & 0.89 & 1.02 & 140.00 \\
lambda.std[17] & 0.78 & 0.05 & 0.68 & 0.75 & 0.79 & 0.82 & 0.86 & 1.04 & 79.00 \\
lambda.std[18] & 0.67 & 0.06 & 0.55 & 0.63 & 0.67 & 0.70 & 0.77 & 1.03 & 140.00 \\
lambda.std[19] & 0.71 & 0.00 & 0.71 & 0.71 & 0.71 & 0.71 & 0.71 & 1.00 & 1.00 \\
lambda.std[20] & 0.76 & 0.03 & 0.70 & 0.74 & 0.77 & 0.79 & 0.83 & 1.01 & 820.00 \\
lambda.std[21] & 0.69 & 0.04 & 0.61 & 0.66 & 0.69 & 0.72 & 0.76 & 1.00 & 830.00 \\
lambda.std[22] & 0.74 & 0.03 & 0.68 & 0.72 & 0.74 & 0.76 & 0.80 & 1.01 & 220.00 \\
lambda.std[23] & 0.68 & 0.04 & 0.59 & 0.65 & 0.68 & 0.71 & 0.76 & 1.01 & 270.00 \\
lambda.std[24] & 0.67 & 0.04 & 0.60 & 0.65 & 0.67 & 0.69 & 0.74 & 1.01 & 420.00 \\
lambda.std[25] & 0.64 & 0.05 & 0.55 & 0.61 & 0.64 & 0.67 & 0.73 & 1.01 & 240.00 \\
phi[1,1] & 2.59 & 1.41 & 0.72 & 1.51 & 2.33 & 3.38 & 6.13 & 1.01 & 580.00 \\
phi[2,1] & 2.02 & 1.22 & 0.21 & 1.17 & 1.87 & 2.76 & 4.78 & 1.04 & 110.00 \\
phi[3,1] & 1.87 & 1.28 & 0.00 & 1.03 & 1.68 & 2.47 & 4.96 & 1.03 & 210.00 \\
phi[4,1] & 2.16 & 0.96 & 0.25 & 1.51 & 2.17 & 2.82 & 4.00 & 1.01 & 400.00 \\
phi[1,2] & 2.02 & 1.22 & 0.21 & 1.17 & 1.87 & 2.76 & 4.78 & 1.04 & 110.00 \\
phi[2,2] & 3.22 & 2.52 & 0.97 & 1.89 & 2.64 & 3.77 & 9.48 & 1.13 & 32.00 \\
phi[3,2] & 1.78 & 1.28 & -0.60 & 1.03 & 1.73 & 2.47 & 4.35 & 1.04 & 180.00 \\
phi[4,2] & 2.53 & 0.95 & 0.73 & 1.92 & 2.47 & 3.09 & 4.44 & 1.09 & 46.00 \\
phi[1,3] & 1.87 & 1.28 & 0.00 & 1.03 & 1.68 & 2.47 & 4.96 & 1.03 & 210.00 \\
phi[2,3] & 1.78 & 1.28 & -0.60 & 1.03 & 1.73 & 2.47 & 4.35 & 1.04 & 180.00 \\
phi[3,3] & 2.59 & 1.68 & 0.70 & 1.54 & 2.23 & 3.14 & 6.44 & 1.04 & 120.00 \\
phi[4,3] & 1.91 & 1.13 & -0.75 & 1.34 & 2.06 & 2.62 & 3.85 & 1.03 & 370.00 \\
phi[1,4] & 2.16 & 0.96 & 0.25 & 1.51 & 2.17 & 2.82 & 4.00 & 1.01 & 400.00 \\
phi[2,4] & 2.53 & 0.95 & 0.73 & 1.92 & 2.47 & 3.09 & 4.44 & 1.09 & 46.00 \\
phi[3,4] & 1.91 & 1.13 & -0.75 & 1.34 & 2.06 & 2.62 & 3.85 & 1.03 & 370.00 \\
phi[4,4] & 2.96 & 0.31 & 2.41 & 2.74 & 2.94 & 3.17 & 3.59 & 1.01 & 220.00 \\
phi.cor[1,1] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[2,1] & 0.73 & 0.22 & 0.13 & 0.66 & 0.80 & 0.88 & 0.95 & 1.07 & 100.00 \\
phi.cor[3,1] & 0.72 & 0.24 & 0.00 & 0.65 & 0.79 & 0.88 & 0.95 & 1.02 & 170.00 \\
phi.cor[4,1] & 0.78 & 0.21 & 0.12 & 0.73 & 0.86 & 0.91 & 0.96 & 1.07 & 120.00 \\
phi.cor[1,2] & 0.73 & 0.22 & 0.13 & 0.66 & 0.80 & 0.88 & 0.95 & 1.07 & 100.00 \\
phi.cor[2,2] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[3,2] & 0.65 & 0.30 & -0.25 & 0.57 & 0.76 & 0.85 & 0.93 & 1.05 & 170.00 \\
phi.cor[4,2] & 0.84 & 0.15 & 0.40 & 0.82 & 0.89 & 0.93 & 0.97 & 1.04 & 160.00 \\
phi.cor[1,3] & 0.72 & 0.24 & 0.00 & 0.65 & 0.79 & 0.88 & 0.95 & 1.02 & 170.00 \\
phi.cor[2,3] & 0.65 & 0.30 & -0.25 & 0.57 & 0.76 & 0.85 & 0.93 & 1.05 & 170.00 \\
phi.cor[3,3] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
phi.cor[4,3] & 0.70 & 0.32 & -0.35 & 0.66 & 0.82 & 0.89 & 0.95 & 1.06 & 97.00 \\
phi.cor[1,4] & 0.78 & 0.21 & 0.12 & 0.73 & 0.86 & 0.91 & 0.96 & 1.07 & 120.00 \\
phi.cor[2,4] & 0.84 & 0.15 & 0.40 & 0.82 & 0.89 & 0.93 & 0.97 & 1.04 & 160.00 \\
phi.cor[3,4] & 0.70 & 0.32 & -0.35 & 0.66 & 0.82 & 0.89 & 0.95 & 1.06 & 97.00 \\
phi.cor[4,4] & 1.00 & 0.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 & 1.00 \\
reli.omega[1] & 0.91 & 0.01 & 0.89 & 0.90 & 0.91 & 0.92 & 0.93 & 1.01 & 660.00 \\
reli.omega[2] & 0.82 & 0.01 & 0.80 & 0.82 & 0.82 & 0.83 & 0.85 & 1.03 & 95.00 \\
reli.omega[3] & 0.85 & 0.02 & 0.81 & 0.84 & 0.85 & 0.87 & 0.89 & 1.02 & 230.00 \\
reli.omega[4] & 0.86 & 0.01 & 0.84 & 0.85 & 0.86 & 0.87 & 0.88 & 1.02 & 190.00 \\
tau[1,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[2,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[3,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[4,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[5,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[6,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[7,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[8,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[9,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[10,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[11,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[12,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[13,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[14,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[15,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[16,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[17,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[18,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[19,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[20,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[21,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[22,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[23,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[24,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[25,1] & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00 & 1.00 \\
tau[1,2] & 3.13 & 0.17 & 2.80 & 3.01 & 3.12 & 3.24 & 3.45 & 1.00 & 890.00 \\
tau[2,2] & 4.01 & 0.36 & 3.38 & 3.75 & 3.99 & 4.24 & 4.81 & 1.01 & 230.00 \\
tau[3,2] & 3.62 & 0.32 & 3.04 & 3.40 & 3.61 & 3.83 & 4.28 & 1.00 & 2500.00 \\
tau[4,2] & 2.21 & 0.18 & 1.87 & 2.09 & 2.20 & 2.32 & 2.58 & 1.02 & 150.00 \\
tau[5,2] & 2.74 & 0.21 & 2.35 & 2.59 & 2.73 & 2.87 & 3.16 & 1.01 & 540.00 \\
tau[6,2] & 3.16 & 0.25 & 2.68 & 2.98 & 3.14 & 3.32 & 3.69 & 1.01 & 420.00 \\
tau[7,2] & 4.33 & 0.39 & 3.64 & 4.05 & 4.30 & 4.57 & 5.17 & 1.01 & 240.00 \\
tau[8,2] & 2.05 & 0.13 & 1.80 & 1.96 & 2.05 & 2.14 & 2.31 & 1.00 & 1300.00 \\
tau[9,2] & 0.95 & 0.14 & 0.66 & 0.87 & 0.97 & 1.05 & 1.20 & 1.00 & 4000.00 \\
tau[10,2] & 1.51 & 0.11 & 1.29 & 1.43 & 1.51 & 1.59 & 1.74 & 1.00 & 890.00 \\
tau[11,2] & 0.08 & 0.06 & 0.00 & 0.03 & 0.06 & 0.12 & 0.23 & 1.00 & 4000.00 \\
tau[12,2] & 1.75 & 0.11 & 1.53 & 1.67 & 1.74 & 1.82 & 1.97 & 1.00 & 680.00 \\
tau[13,2] & 1.81 & 0.10 & 1.61 & 1.74 & 1.81 & 1.88 & 2.01 & 1.00 & 4000.00 \\
tau[14,2] & 2.92 & 0.22 & 2.52 & 2.76 & 2.92 & 3.07 & 3.38 & 1.01 & 230.00 \\
tau[15,2] & 1.42 & 0.14 & 1.17 & 1.33 & 1.42 & 1.52 & 1.70 & 1.00 & 1100.00 \\
tau[16,2] & 4.98 & 0.54 & 4.05 & 4.60 & 4.94 & 5.32 & 6.11 & 1.03 & 100.00 \\
tau[17,2] & 3.80 & 0.34 & 3.18 & 3.55 & 3.78 & 4.02 & 4.52 & 1.04 & 81.00 \\
tau[18,2] & 3.22 & 0.25 & 2.74 & 3.05 & 3.21 & 3.38 & 3.73 & 1.01 & 340.00 \\
tau[19,2] & 2.15 & 0.11 & 1.93 & 2.07 & 2.15 & 2.23 & 2.37 & 1.00 & 1600.00 \\
tau[20,2] & 2.99 & 0.21 & 2.61 & 2.84 & 2.97 & 3.12 & 3.42 & 1.00 & 560.00 \\
tau[21,2] & 1.77 & 0.12 & 1.54 & 1.69 & 1.77 & 1.85 & 2.01 & 1.00 & 2200.00 \\
tau[22,2] & 2.15 & 0.14 & 1.90 & 2.06 & 2.15 & 2.24 & 2.43 & 1.00 & 1000.00 \\
tau[23,2] & 0.14 & 0.08 & 0.01 & 0.07 & 0.14 & 0.19 & 0.30 & 1.00 & 4000.00 \\
tau[24,2] & 1.98 & 0.12 & 1.75 & 1.89 & 1.98 & 2.06 & 2.23 & 1.00 & 2100.00 \\
tau[25,2] & 0.05 & 0.04 & 0.00 & 0.02 & 0.03 & 0.07 & 0.14 & 1.00 & 1100.00 \\
theta[1] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[2] & 3.16 & 0.54 & 2.27 & 2.77 & 3.09 & 3.49 & 4.39 & 1.01 & 540.00 \\
theta[3] & 2.88 & 0.50 & 2.10 & 2.52 & 2.81 & 3.16 & 4.01 & 1.01 & 510.00 \\
theta[4] & 2.04 & 0.27 & 1.58 & 1.86 & 2.02 & 2.20 & 2.67 & 1.03 & 100.00 \\
theta[5] & 2.29 & 0.29 & 1.82 & 2.08 & 2.26 & 2.47 & 2.91 & 1.01 & 570.00 \\
theta[6] & 2.20 & 0.30 & 1.70 & 1.99 & 2.17 & 2.38 & 2.85 & 1.01 & 220.00 \\
theta[7] & 3.04 & 0.53 & 2.21 & 2.64 & 2.96 & 3.36 & 4.23 & 1.01 & 350.00 \\
theta[8] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[9] & 1.76 & 0.17 & 1.47 & 1.64 & 1.74 & 1.86 & 2.11 & 1.02 & 140.00 \\
theta[10] & 1.58 & 0.15 & 1.34 & 1.48 & 1.56 & 1.67 & 1.93 & 1.01 & 270.00 \\
theta[11] & 1.59 & 0.16 & 1.33 & 1.48 & 1.57 & 1.69 & 1.95 & 1.01 & 290.00 \\
theta[12] & 1.86 & 0.16 & 1.59 & 1.74 & 1.85 & 1.96 & 2.23 & 1.01 & 280.00 \\
theta[13] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[14] & 1.70 & 0.22 & 1.33 & 1.55 & 1.68 & 1.84 & 2.18 & 1.02 & 120.00 \\
theta[15] & 1.25 & 0.08 & 1.13 & 1.19 & 1.23 & 1.29 & 1.42 & 1.02 & 180.00 \\
theta[16] & 3.02 & 0.71 & 1.93 & 2.50 & 2.92 & 3.43 & 4.68 & 1.03 & 110.00 \\
theta[17] & 2.72 & 0.55 & 1.86 & 2.29 & 2.64 & 3.11 & 3.88 & 1.04 & 68.00 \\
theta[18] & 1.84 & 0.26 & 1.43 & 1.66 & 1.81 & 1.99 & 2.46 & 1.02 & 200.00 \\
theta[19] & 2.00 & 0.00 & 2.00 & 2.00 & 2.00 & 2.00 & 2.00 & 1.00 & 1.00 \\
theta[20] & 2.45 & 0.31 & 1.94 & 2.23 & 2.42 & 2.64 & 3.17 & 1.01 & 710.00 \\
theta[21] & 1.93 & 0.20 & 1.59 & 1.78 & 1.91 & 2.05 & 2.36 & 1.00 & 920.00 \\
theta[22] & 2.24 & 0.23 & 1.86 & 2.08 & 2.23 & 2.38 & 2.74 & 1.01 & 250.00 \\
theta[23] & 1.89 & 0.21 & 1.53 & 1.74 & 1.86 & 2.01 & 2.39 & 1.01 & 270.00 \\
theta[24] & 1.84 & 0.17 & 1.57 & 1.72 & 1.82 & 1.93 & 2.23 & 1.01 & 450.00 \\
theta[25] & 1.72 & 0.17 & 1.43 & 1.59 & 1.70 & 1.82 & 2.11 & 1.01 & 280.00 \\
\bottomrule
\end{tabular}
\caption{pools Model 3 posterior distribution summary}
\end{table}
sessionInfo()R version 4.0.5 (2021-03-31)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 22000)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.1252
[2] LC_CTYPE=English_United States.1252
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] readxl_1.3.1 car_3.0-10 carData_3.0-4
[4] mvtnorm_1.1-1 LaplacesDemon_16.1.4 runjags_2.2.0-2
[7] lme4_1.1-26 Matrix_1.3-2 sirt_3.9-4
[10] R2jags_0.6-1 rjags_4-12 eRm_1.0-2
[13] diffIRT_1.5 statmod_1.4.35 xtable_1.8-4
[16] kableExtra_1.3.4 lavaan_0.6-7 polycor_0.7-10
[19] bayesplot_1.8.0 ggmcmc_1.5.1.1 coda_0.19-4
[22] data.table_1.14.0 patchwork_1.1.1 forcats_0.5.1
[25] stringr_1.4.0 dplyr_1.0.5 purrr_0.3.4
[28] readr_1.4.0 tidyr_1.1.3 tibble_3.1.0
[31] ggplot2_3.3.5 tidyverse_1.3.0 workflowr_1.6.2
loaded via a namespace (and not attached):
[1] minqa_1.2.4 TAM_3.5-19 colorspace_2.0-0 rio_0.5.26
[5] ellipsis_0.3.1 ggridges_0.5.3 rprojroot_2.0.2 fs_1.5.0
[9] rstudioapi_0.13 farver_2.1.0 fansi_0.4.2 lubridate_1.7.10
[13] xml2_1.3.2 splines_4.0.5 mnormt_2.0.2 knitr_1.31
[17] jsonlite_1.7.2 nloptr_1.2.2.2 broom_0.7.5 dbplyr_2.1.0
[21] compiler_4.0.5 httr_1.4.2 backports_1.2.1 assertthat_0.2.1
[25] cli_2.3.1 later_1.1.0.1 htmltools_0.5.1.1 tools_4.0.5
[29] gtable_0.3.0 glue_1.4.2 reshape2_1.4.4 Rcpp_1.0.7
[33] cellranger_1.1.0 jquerylib_0.1.3 vctrs_0.3.6 svglite_2.0.0
[37] nlme_3.1-152 psych_2.0.12 xfun_0.21 ps_1.6.0
[41] openxlsx_4.2.3 rvest_1.0.0 lifecycle_1.0.0 MASS_7.3-53.1
[45] scales_1.1.1 ragg_1.1.1 hms_1.0.0 promises_1.2.0.1
[49] parallel_4.0.5 RColorBrewer_1.1-2 curl_4.3 yaml_2.2.1
[53] sass_0.3.1 reshape_0.8.8 stringi_1.5.3 highr_0.8
[57] zip_2.1.1 boot_1.3-27 rlang_0.4.10 pkgconfig_2.0.3
[61] systemfonts_1.0.1 evaluate_0.14 lattice_0.20-41 labeling_0.4.2
[65] tidyselect_1.1.0 GGally_2.1.1 plyr_1.8.6 magrittr_2.0.1
[69] R6_2.5.0 generics_0.1.0 DBI_1.1.1 foreign_0.8-81
[73] pillar_1.5.1 haven_2.3.1 withr_2.4.1 abind_1.4-5
[77] modelr_0.1.8 crayon_1.4.1 utf8_1.1.4 tmvnsim_1.0-2
[81] rmarkdown_2.7 grid_4.0.5 CDM_7.5-15 pbivnorm_0.6.0
[85] git2r_0.28.0 reprex_1.0.0 digest_0.6.27 webshot_0.5.2
[89] httpuv_1.5.5 textshaping_0.3.1 stats4_4.0.5 munsell_0.5.0
[93] viridisLite_0.3.0 bslib_0.2.4 R2WinBUGS_2.1-21