POOLS Development: Exploratory Factor Analysis

workflowr

• Summary
• Checks
• Past versions

Last updated: 2021-02-18

Checks: 7 0

Knit directory: pools-projects/

This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

---

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20201007)

The command set.seed(20201007) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 5934257

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 5934257. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:

Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/

Untracked files:
    Untracked:  manuscript/pools-development-paper-2021-02-18-blind.docx
    Untracked:  manuscript/pools-development-paper-2021-02-18-title-page.docx

Unstaged changes:
    Modified:   .Rprofile
    Deleted:    .gitattributes
    Modified:   .gitignore
    Modified:   manuscript/pools-development-paper-2021-02-18.docx
    Modified:   manuscript/~$ols-development-paper-2021-02-18.docx

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

---

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/development-study-EFA.Rmd) and HTML (docs/development-study-EFA.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	5934257	noah-padgett	2021-02-18	major revision to structure
html	5934257	noah-padgett	2021-02-18	major revision to structure

---

Prior Expectations

Prior to conducting the EFA, we expect that the four factors will emerge from a four-factor solution.

Data

source("code/load_packages.R")

mydata <- read.table("data/data-2020-11-16/pools_data_split1_2020_11_16.txt", sep="\t", header=T)
dat <- mydata[,7:63]
cov.dat <- cov(dat)

# setup output object
out.dat <- data.frame(matrix(0, nrow=57, ncol=10))
rownames(out.dat) <- colnames(dat)
colnames(out.dat) <- c("Diff", "SD", "ITCc", "ITCT", "f1", "f2", "f3", "f4", "h2", "u2")

Item Analysis

For the basic item analysis, we conducted these by the a priori item groups to get a sense of how the initially proposed items fit together.

All Items

fit <- psychometric::item.exam(dat)

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q4_1	0.866	0.638	0.622	2.460	0.552	0.538
Q4_2	0.819	0.681	0.667	2.305	0.557	0.546
Q4_3	0.834	0.645	0.631	2.537	0.538	0.525
Q4_4	0.816	0.705	0.692	2.640	0.574	0.564
Q4_5	0.880	0.676	0.661	2.320	0.594	0.581
Q4_6	0.981	0.659	0.642	2.872	0.645	0.629
Q4_7	0.938	0.546	0.526	3.582	0.512	0.493
Q4_8	0.927	0.655	0.639	2.287	0.606	0.591
Q4_9	1.007	0.614	0.595	2.463	0.617	0.598
Q4_10	0.789	0.663	0.650	2.582	0.523	0.512
Q4_11	0.955	0.729	0.715	2.500	0.694	0.681
Q4_12	1.051	0.653	0.635	2.195	0.685	0.666
Q4_13	0.876	0.584	0.566	1.595	0.511	0.495
Q4_14	0.895	0.697	0.683	2.659	0.622	0.610
Q4_15	0.917	0.722	0.708	2.375	0.661	0.648
Q4_16	0.941	0.661	0.645	2.457	0.621	0.606
Q4_17	0.964	0.631	0.614	2.198	0.608	0.591
Q4_18	0.823	0.737	0.726	2.360	0.606	0.597
Q4_19	0.970	0.733	0.719	2.543	0.709	0.696
Q5_1	0.951	0.652	0.635	2.637	0.619	0.603
Q5_2	1.035	0.643	0.624	2.954	0.664	0.645
Q5_3	1.046	0.649	0.631	2.662	0.678	0.659
Q5_4	1.106	0.566	0.543	3.500	0.625	0.600
Q5_5	1.034	0.495	0.471	3.530	0.511	0.486
Q5_6	0.906	0.686	0.671	2.927	0.620	0.607
Q5_7	0.942	0.636	0.619	2.704	0.598	0.582
Q5_8	1.055	0.667	0.649	2.905	0.703	0.684
Q5_9	0.995	0.728	0.714	2.610	0.724	0.709
Q5_10	0.837	0.610	0.594	2.622	0.510	0.496
Q5_11	0.951	0.674	0.658	2.707	0.640	0.625
Q5_12	0.952	0.660	0.644	2.881	0.627	0.612
Q6_1	0.844	0.526	0.508	1.701	0.443	0.428
Q6_2	0.912	0.581	0.563	2.079	0.529	0.512
Q6_3	0.924	0.561	0.542	1.930	0.518	0.500
Q6_4	0.927	0.510	0.490	2.076	0.473	0.453
Q6_5	1.033	0.495	0.472	2.351	0.511	0.486
Q6_6	0.820	0.641	0.626	1.832	0.525	0.513
Q6_7	0.875	0.680	0.666	2.162	0.594	0.582
Q6_8	0.903	0.630	0.613	2.113	0.568	0.553
Q6_9	1.222	0.532	0.505	2.768	0.649	0.616
Q6_10	0.913	0.593	0.575	2.887	0.541	0.524
Q6_11	0.970	0.714	0.699	2.814	0.691	0.677
Q7_1	0.901	0.758	0.746	2.463	0.682	0.671
Q7_2	0.857	0.693	0.679	2.692	0.592	0.581
Q7_3	1.012	0.575	0.555	3.558	0.581	0.561
Q7_4	0.980	0.628	0.610	2.841	0.614	0.597
Q7_5	0.948	0.719	0.705	2.875	0.681	0.668
Q7_6	0.920	0.679	0.664	2.933	0.624	0.610
Q7_7	1.014	0.598	0.579	3.652	0.606	0.586
Q7_8	0.877	0.634	0.618	2.814	0.555	0.542
Q7_9	0.993	0.710	0.695	2.567	0.704	0.689
Q7_10	0.945	0.715	0.701	2.280	0.675	0.661
Q7_11	0.840	0.671	0.657	2.744	0.562	0.550
Q7_12	1.023	0.556	0.535	3.390	0.568	0.546
Q7_13	0.989	0.300	0.273	3.579	0.296	0.269
Q7_14	0.986	0.454	0.430	3.610	0.447	0.424
Q7_15	0.905	0.663	0.648	2.509	0.600	0.586

out.dat[, c(1,2, 4)] <- fit[, c(4, 1, 3)]

Initial Effective Learning Items

Item Analysis

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q4_",1:19)])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q4_1	0.866	0.750	0.717	2.460	0.649	0.621
Q4_2	0.819	0.789	0.763	2.305	0.646	0.624
Q4_3	0.834	0.744	0.712	2.537	0.620	0.593
Q4_4	0.816	0.772	0.743	2.640	0.629	0.605
Q4_5	0.880	0.731	0.696	2.320	0.643	0.612
Q4_6	0.981	0.650	0.601	2.872	0.637	0.589
Q4_7	0.938	0.515	0.457	3.582	0.483	0.428
Q4_8	0.927	0.777	0.745	2.287	0.719	0.690
Q4_9	1.007	0.701	0.657	2.463	0.705	0.660
Q4_10	0.789	0.730	0.698	2.582	0.575	0.550
Q4_11	0.955	0.792	0.761	2.500	0.755	0.725
Q4_12	1.051	0.696	0.649	2.195	0.730	0.681
Q4_13	0.876	0.650	0.607	1.595	0.569	0.531
Q4_14	0.895	0.716	0.679	2.659	0.640	0.607
Q4_15	0.917	0.789	0.759	2.375	0.722	0.695
Q4_16	0.941	0.726	0.688	2.457	0.682	0.646
Q4_17	0.964	0.720	0.680	2.198	0.694	0.655
Q4_18	0.823	0.843	0.822	2.360	0.693	0.676
Q4_19	0.970	0.793	0.762	2.543	0.768	0.738

out.dat[1:19, 3] <- fit[, 3]

Preliminary Reliability

# preliminary reliability
psych::alpha(dat[, paste0("Q4_",1:19)])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q4_", 1:19)])

  raw_alpha std.alpha G6(smc) average_r S/N   ase mean   sd median_r
      0.95      0.95    0.96      0.51  20 0.004  2.5 0.66     0.51

 lower alpha upper     95% confidence boundaries
0.94 0.95 0.96 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
Q4_1       0.95      0.95    0.96      0.51  18   0.0042 0.0103  0.51
Q4_2       0.95      0.95    0.96      0.50  18   0.0043 0.0103  0.51
Q4_3       0.95      0.95    0.96      0.51  18   0.0042 0.0101  0.51
Q4_4       0.95      0.95    0.96      0.50  18   0.0042 0.0105  0.51
Q4_5       0.95      0.95    0.96      0.51  19   0.0042 0.0109  0.51
Q4_6       0.95      0.95    0.96      0.52  19   0.0041 0.0105  0.53
Q4_7       0.95      0.95    0.96      0.53  20   0.0039 0.0069  0.53
Q4_8       0.95      0.95    0.96      0.50  18   0.0043 0.0106  0.51
Q4_9       0.95      0.95    0.96      0.51  19   0.0041 0.0104  0.52
Q4_10      0.95      0.95    0.96      0.51  19   0.0042 0.0108  0.51
Q4_11      0.95      0.95    0.96      0.50  18   0.0043 0.0108  0.51
Q4_12      0.95      0.95    0.96      0.51  19   0.0041 0.0105  0.52
Q4_13      0.95      0.95    0.96      0.52  19   0.0041 0.0094  0.52
Q4_14      0.95      0.95    0.96      0.51  19   0.0042 0.0109  0.52
Q4_15      0.95      0.95    0.96      0.50  18   0.0043 0.0103  0.51
Q4_16      0.95      0.95    0.96      0.51  19   0.0042 0.0107  0.52
Q4_17      0.95      0.95    0.96      0.51  19   0.0042 0.0108  0.52
Q4_18      0.95      0.95    0.96      0.50  18   0.0043 0.0096  0.50
Q4_19      0.95      0.95    0.96      0.50  18   0.0043 0.0105  0.51

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q4_1  328  0.75  0.76  0.74   0.72  2.5 0.87
Q4_2  328  0.79  0.80  0.79   0.76  2.3 0.82
Q4_3  328  0.74  0.75  0.74   0.71  2.5 0.83
Q4_4  328  0.77  0.78  0.77   0.74  2.6 0.82
Q4_5  328  0.73  0.73  0.72   0.70  2.3 0.88
Q4_6  328  0.65  0.65  0.62   0.60  2.9 0.98
Q4_7  328  0.52  0.51  0.48   0.46  3.6 0.94
Q4_8  328  0.78  0.78  0.76   0.75  2.3 0.93
Q4_9  328  0.70  0.70  0.68   0.66  2.5 1.01
Q4_10 328  0.73  0.74  0.72   0.70  2.6 0.79
Q4_11 328  0.79  0.79  0.78   0.76  2.5 0.95
Q4_12 328  0.70  0.69  0.67   0.65  2.2 1.05
Q4_13 328  0.65  0.65  0.63   0.61  1.6 0.88
Q4_14 328  0.72  0.72  0.70   0.68  2.7 0.89
Q4_15 328  0.79  0.79  0.78   0.76  2.4 0.92
Q4_16 328  0.73  0.72  0.71   0.69  2.5 0.94
Q4_17 328  0.72  0.72  0.70   0.68  2.2 0.96
Q4_18 328  0.84  0.85  0.84   0.82  2.4 0.82
Q4_19 328  0.79  0.79  0.78   0.76  2.5 0.97

Non missing response frequency for each item
         1    2    3    4    5 miss
Q4_1  0.13 0.38 0.39 0.09 0.01    0
Q4_2  0.15 0.47 0.32 0.05 0.01    0
Q4_3  0.10 0.37 0.44 0.08 0.02    0
Q4_4  0.09 0.28 0.54 0.08 0.02    0
Q4_5  0.16 0.47 0.28 0.08 0.01    0
Q4_6  0.09 0.23 0.44 0.20 0.05    0
Q4_7  0.04 0.09 0.24 0.52 0.11    0
Q4_8  0.20 0.43 0.28 0.07 0.02    0
Q4_9  0.15 0.42 0.27 0.12 0.04    0
Q4_10 0.09 0.30 0.54 0.04 0.02    0
Q4_11 0.16 0.34 0.38 0.10 0.02    0
Q4_12 0.28 0.40 0.18 0.11 0.03    0
Q4_13 0.59 0.29 0.08 0.02 0.02    0
Q4_14 0.11 0.27 0.50 0.09 0.03    0
Q4_15 0.16 0.41 0.33 0.07 0.02    0
Q4_16 0.17 0.33 0.40 0.08 0.02    0
Q4_17 0.26 0.39 0.25 0.08 0.02    0
Q4_18 0.13 0.47 0.34 0.06 0.01    0
Q4_19 0.14 0.35 0.39 0.08 0.04    0

Initial Student Centered Items

Item Analayis

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q5_",1:12)])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q5_1	0.951	0.700	0.636	2.637	0.665	0.604
Q5_2	1.035	0.742	0.680	2.954	0.767	0.703
Q5_3	1.046	0.770	0.713	2.662	0.804	0.744
Q5_4	1.106	0.732	0.663	3.500	0.808	0.732
Q5_5	1.034	0.680	0.607	3.530	0.702	0.627
Q5_6	0.906	0.809	0.768	2.927	0.732	0.694
Q5_7	0.942	0.672	0.605	2.704	0.632	0.569
Q5_8	1.055	0.800	0.748	2.905	0.842	0.788
Q5_9	0.995	0.779	0.726	2.610	0.774	0.722
Q5_10	0.837	0.667	0.607	2.622	0.557	0.508
Q5_11	0.951	0.665	0.596	2.707	0.631	0.566
Q5_12	0.952	0.708	0.646	2.881	0.673	0.614

out.dat[20:31, 3] <- fit[, 3]

Preliminary Reliability

# preliminary reliability
psych::alpha(dat[, paste0("Q5_",1:12)])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q5_", 1:12)])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.92      0.92    0.93      0.49  11 0.0066  2.9 0.72     0.48

 lower alpha upper     95% confidence boundaries
0.91 0.92 0.93 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r  S/N alpha se  var.r med.r
Q5_1       0.91      0.91    0.92      0.49 10.6   0.0071 0.0087  0.48
Q5_2       0.91      0.91    0.92      0.48 10.3   0.0073 0.0085  0.48
Q5_3       0.91      0.91    0.92      0.48 10.1   0.0074 0.0081  0.47
Q5_4       0.91      0.91    0.92      0.49 10.4   0.0071 0.0069  0.49
Q5_5       0.91      0.92    0.92      0.49 10.8   0.0070 0.0056  0.49
Q5_6       0.91      0.91    0.92      0.47  9.9   0.0075 0.0078  0.47
Q5_7       0.91      0.91    0.92      0.49 10.7   0.0070 0.0083  0.49
Q5_8       0.91      0.91    0.92      0.48 10.0   0.0075 0.0083  0.47
Q5_9       0.91      0.91    0.92      0.48 10.0   0.0074 0.0084  0.47
Q5_10      0.91      0.91    0.92      0.49 10.7   0.0070 0.0086  0.49
Q5_11      0.91      0.92    0.92      0.50 10.8   0.0070 0.0085  0.49
Q5_12      0.91      0.91    0.92      0.49 10.5   0.0071 0.0094  0.48

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q5_1  328  0.70  0.70  0.67   0.64  2.6 0.95
Q5_2  328  0.74  0.74  0.71   0.68  3.0 1.04
Q5_3  328  0.77  0.77  0.75   0.71  2.7 1.05
Q5_4  328  0.73  0.72  0.71   0.66  3.5 1.11
Q5_5  328  0.68  0.67  0.66   0.61  3.5 1.03
Q5_6  328  0.81  0.81  0.80   0.77  2.9 0.91
Q5_7  328  0.67  0.68  0.64   0.60  2.7 0.94
Q5_8  328  0.80  0.80  0.78   0.75  2.9 1.06
Q5_9  328  0.78  0.78  0.76   0.73  2.6 1.00
Q5_10 328  0.67  0.68  0.64   0.61  2.6 0.84
Q5_11 328  0.66  0.67  0.63   0.60  2.7 0.95
Q5_12 328  0.71  0.71  0.67   0.65  2.9 0.95

Non missing response frequency for each item
         1    2    3    4    5 miss
Q5_1  0.12 0.32 0.40 0.14 0.03    0
Q5_2  0.10 0.20 0.38 0.27 0.05    0
Q5_3  0.15 0.29 0.35 0.17 0.04    0
Q5_4  0.08 0.11 0.21 0.46 0.15    0
Q5_5  0.05 0.12 0.21 0.48 0.14    0
Q5_6  0.09 0.15 0.52 0.21 0.02    0
Q5_7  0.13 0.22 0.51 0.11 0.03    0
Q5_8  0.12 0.19 0.39 0.24 0.05    0
Q5_9  0.14 0.32 0.37 0.14 0.03    0
Q5_10 0.13 0.21 0.59 0.06 0.02    0
Q5_11 0.11 0.30 0.41 0.17 0.02    0
Q5_12 0.10 0.17 0.50 0.19 0.04    0

Initial Interactive Items

Item Analysis

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q6_",1:11)])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q6_1	0.844	0.722	0.660	1.701	0.608	0.556
Q6_2	0.912	0.780	0.725	2.079	0.711	0.660
Q6_3	0.924	0.767	0.708	1.930	0.708	0.653
Q6_4	0.927	0.723	0.654	2.076	0.669	0.606
Q6_5	1.033	0.590	0.487	2.351	0.608	0.502
Q6_6	0.820	0.797	0.751	1.832	0.653	0.615
Q6_7	0.875	0.832	0.790	2.162	0.727	0.690
Q6_8	0.903	0.818	0.770	2.113	0.738	0.695
Q6_9	1.222	0.581	0.455	2.768	0.709	0.556
Q6_10	0.913	0.625	0.541	2.887	0.570	0.493
Q6_11	0.970	0.706	0.630	2.814	0.684	0.610

out.dat[32:42, 3] <- fit[, 3]

Preliminary Reliability

# preliminary reliability
psych::alpha(dat[, paste0("Q6_",1:11)])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q6_", 1:11)])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
       0.9      0.91    0.92      0.47 9.9 0.0082  2.2 0.67     0.44

 lower alpha upper     95% confidence boundaries
0.89 0.9 0.92 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r  S/N alpha se var.r med.r
Q6_1       0.89      0.90    0.91      0.47  9.0   0.0091 0.022  0.43
Q6_2       0.89      0.90    0.91      0.46  8.6   0.0093 0.020  0.43
Q6_3       0.89      0.90    0.91      0.46  8.7   0.0093 0.020  0.43
Q6_4       0.89      0.90    0.91      0.47  9.0   0.0090 0.020  0.43
Q6_5       0.90      0.91    0.92      0.50 10.0   0.0082 0.023  0.56
Q6_6       0.89      0.89    0.91      0.46  8.5   0.0094 0.023  0.42
Q6_7       0.89      0.89    0.91      0.45  8.3   0.0097 0.023  0.42
Q6_8       0.89      0.89    0.91      0.46  8.4   0.0096 0.023  0.42
Q6_9       0.91      0.91    0.92      0.51 10.2   0.0077 0.020  0.56
Q6_10      0.90      0.91    0.92      0.49  9.7   0.0086 0.024  0.53
Q6_11      0.89      0.90    0.91      0.48  9.2   0.0090 0.026  0.44

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q6_1  328  0.72  0.73  0.71   0.66  1.7 0.84
Q6_2  328  0.78  0.79  0.78   0.72  2.1 0.91
Q6_3  328  0.77  0.78  0.77   0.71  1.9 0.92
Q6_4  328  0.72  0.74  0.72   0.65  2.1 0.93
Q6_5  328  0.59  0.58  0.51   0.49  2.4 1.03
Q6_6  328  0.80  0.81  0.79   0.75  1.8 0.82
Q6_7  328  0.83  0.84  0.83   0.79  2.2 0.88
Q6_8  328  0.82  0.82  0.81   0.77  2.1 0.90
Q6_9  328  0.58  0.55  0.49   0.46  2.8 1.22
Q6_10 328  0.63  0.62  0.57   0.54  2.9 0.91
Q6_11 328  0.71  0.70  0.66   0.63  2.8 0.97

Non missing response frequency for each item
         1    2    3    4    5 miss
Q6_1  0.49 0.36 0.09 0.05 0.00    0
Q6_2  0.27 0.47 0.17 0.07 0.01    0
Q6_3  0.36 0.45 0.13 0.05 0.02    0
Q6_4  0.29 0.43 0.20 0.06 0.01    0
Q6_5  0.19 0.46 0.21 0.10 0.04    0
Q6_6  0.37 0.48 0.11 0.03 0.01    0
Q6_7  0.21 0.50 0.20 0.07 0.01    0
Q6_8  0.25 0.47 0.20 0.07 0.01    0
Q6_9  0.16 0.28 0.30 0.14 0.12    0
Q6_10 0.10 0.15 0.57 0.15 0.04    0
Q6_11 0.11 0.21 0.49 0.14 0.05    0

Initial Engagement Items

Item Analysis

fit <- psychometric::item.exam(dat[, paste0("Q7_",1:15)])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q7_1	0.901	0.748	0.703	2.463	0.673	0.633
Q7_2	0.857	0.738	0.694	2.692	0.631	0.594
Q7_3	1.012	0.712	0.656	3.558	0.720	0.663
Q7_4	0.980	0.732	0.681	2.841	0.716	0.666
Q7_5	0.948	0.808	0.770	2.875	0.765	0.729
Q7_6	0.920	0.745	0.699	2.933	0.684	0.642
Q7_7	1.014	0.736	0.683	3.652	0.745	0.692
Q7_8	0.877	0.731	0.685	2.814	0.640	0.600
Q7_9	0.993	0.716	0.662	2.567	0.710	0.656
Q7_10	0.945	0.686	0.631	2.280	0.648	0.595
Q7_11	0.840	0.745	0.704	2.744	0.625	0.590
Q7_12	1.023	0.674	0.611	3.390	0.688	0.624
Q7_13	0.989	0.454	0.370	3.579	0.449	0.365
Q7_14	0.986	0.605	0.535	3.610	0.595	0.527
Q7_15	0.905	0.665	0.609	2.509	0.601	0.550

out.dat[43:57, 3] <- fit[, 3]

Preliminary Reliability

# preliminary reliability
psych::alpha(dat[, paste0("Q7_",1:15)])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q7_", 1:15)])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.92      0.93    0.94      0.45  12 0.0062    3 0.66     0.47

 lower alpha upper     95% confidence boundaries
0.91 0.92 0.94 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
Q7_1       0.92      0.92    0.93      0.45  11   0.0067 0.017  0.47
Q7_2       0.92      0.92    0.94      0.45  11   0.0067 0.018  0.47
Q7_3       0.92      0.92    0.93      0.45  12   0.0066 0.017  0.48
Q7_4       0.92      0.92    0.94      0.45  11   0.0067 0.017  0.47
Q7_5       0.92      0.92    0.93      0.44  11   0.0069 0.017  0.46
Q7_6       0.92      0.92    0.94      0.45  11   0.0067 0.018  0.46
Q7_7       0.92      0.92    0.93      0.45  11   0.0067 0.017  0.48
Q7_8       0.92      0.92    0.94      0.45  11   0.0067 0.018  0.47
Q7_9       0.92      0.92    0.94      0.45  12   0.0066 0.017  0.47
Q7_10      0.92      0.92    0.93      0.45  12   0.0065 0.015  0.47
Q7_11      0.92      0.92    0.93      0.45  11   0.0067 0.018  0.47
Q7_12      0.92      0.92    0.94      0.46  12   0.0065 0.019  0.49
Q7_13      0.93      0.93    0.94      0.48  13   0.0059 0.011  0.50
Q7_14      0.92      0.92    0.94      0.47  12   0.0063 0.017  0.49
Q7_15      0.92      0.92    0.94      0.46  12   0.0065 0.016  0.48

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q7_1  328  0.75  0.75  0.74   0.70  2.5 0.90
Q7_2  328  0.74  0.74  0.73   0.69  2.7 0.86
Q7_3  328  0.71  0.71  0.69   0.66  3.6 1.01
Q7_4  328  0.73  0.73  0.71   0.68  2.8 0.98
Q7_5  328  0.81  0.81  0.80   0.77  2.9 0.95
Q7_6  328  0.74  0.75  0.72   0.70  2.9 0.92
Q7_7  328  0.74  0.73  0.72   0.68  3.7 1.01
Q7_8  328  0.73  0.73  0.71   0.69  2.8 0.88
Q7_9  328  0.72  0.72  0.70   0.66  2.6 0.99
Q7_10 328  0.69  0.69  0.68   0.63  2.3 0.95
Q7_11 328  0.75  0.75  0.74   0.70  2.7 0.84
Q7_12 328  0.67  0.67  0.64   0.61  3.4 1.02
Q7_13 328  0.45  0.45  0.39   0.37  3.6 0.99
Q7_14 328  0.60  0.60  0.56   0.54  3.6 0.99
Q7_15 328  0.66  0.67  0.65   0.61  2.5 0.91

Non missing response frequency for each item
         1    2    3    4    5 miss
Q7_1  0.15 0.35 0.40 0.09 0.01    0
Q7_2  0.11 0.21 0.57 0.09 0.02    0
Q7_3  0.05 0.10 0.22 0.50 0.13    0
Q7_4  0.10 0.21 0.47 0.17 0.05    0
Q7_5  0.10 0.18 0.51 0.17 0.04    0
Q7_6  0.08 0.17 0.53 0.18 0.04    0
Q7_7  0.05 0.09 0.17 0.53 0.16    0
Q7_8  0.10 0.17 0.55 0.15 0.02    0
Q7_9  0.16 0.29 0.41 0.12 0.03    0
Q7_10 0.20 0.45 0.25 0.08 0.02    0
Q7_11 0.10 0.19 0.59 0.11 0.02    0
Q7_12 0.07 0.09 0.32 0.43 0.10    0
Q7_13 0.02 0.11 0.32 0.36 0.19    0
Q7_14 0.05 0.08 0.24 0.48 0.15    0
Q7_15 0.14 0.33 0.43 0.08 0.02    0

EFA

Correlations

First, we investigated the raw correlations among the variables.

# Pearson correlation matrix
corr.ppm <- cor(dat)
kable(corr.ppm,digits=3,format = "html")%>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%", height="500px")

	Q4_1	Q4_2	Q4_3	Q4_4	Q4_5	Q4_6	Q4_7	Q4_8	Q4_9	Q4_10	Q4_11	Q4_12	Q4_13	Q4_14	Q4_15	Q4_16	Q4_17	Q4_18	Q4_19	Q5_1	Q5_2	Q5_3	Q5_4	Q5_5	Q5_6	Q5_7	Q5_8	Q5_9	Q5_10	Q5_11	Q5_12	Q6_1	Q6_2	Q6_3	Q6_4	Q6_5	Q6_6	Q6_7	Q6_8	Q6_9	Q6_10	Q6_11	Q7_1	Q7_2	Q7_3	Q7_4	Q7_5	Q7_6	Q7_7	Q7_8	Q7_9	Q7_10	Q7_11	Q7_12	Q7_13	Q7_14	Q7_15
Q4_1	1.000	0.629	0.685	0.672	0.508	0.473	0.316	0.585	0.431	0.568	0.586	0.408	0.408	0.543	0.533	0.540	0.469	0.655	0.495	0.422	0.337	0.362	0.349	0.283	0.394	0.298	0.319	0.432	0.350	0.424	0.330	0.293	0.275	0.235	0.257	0.250	0.290	0.369	0.312	0.245	0.309	0.357	0.458	0.340	0.247	0.331	0.398	0.357	0.287	0.298	0.527	0.495	0.423	0.307	0.127	0.218	0.445
Q4_2	0.629	1.000	0.646	0.636	0.657	0.486	0.341	0.621	0.514	0.552	0.563	0.488	0.518	0.485	0.592	0.501	0.523	0.730	0.561	0.464	0.381	0.414	0.334	0.292	0.413	0.307	0.369	0.446	0.378	0.472	0.368	0.265	0.315	0.271	0.243	0.340	0.390	0.392	0.300	0.266	0.365	0.422	0.483	0.387	0.285	0.342	0.474	0.384	0.352	0.394	0.471	0.505	0.407	0.281	0.129	0.197	0.454
Q4_3	0.685	0.646	1.000	0.680	0.490	0.413	0.326	0.607	0.508	0.597	0.572	0.351	0.370	0.459	0.540	0.512	0.476	0.622	0.577	0.431	0.347	0.356	0.331	0.293	0.429	0.308	0.350	0.448	0.335	0.480	0.292	0.302	0.270	0.247	0.244	0.296	0.302	0.367	0.309	0.245	0.284	0.369	0.449	0.356	0.289	0.303	0.406	0.390	0.377	0.337	0.488	0.479	0.472	0.345	0.148	0.211	0.411
Q4_4	0.672	0.636	0.680	1.000	0.519	0.489	0.430	0.610	0.498	0.645	0.573	0.439	0.381	0.489	0.524	0.526	0.507	0.663	0.530	0.419	0.368	0.348	0.383	0.365	0.473	0.406	0.387	0.429	0.409	0.384	0.437	0.234	0.306	0.299	0.226	0.281	0.408	0.394	0.354	0.290	0.364	0.460	0.469	0.476	0.370	0.487	0.499	0.473	0.403	0.436	0.521	0.516	0.517	0.334	0.134	0.308	0.477
Q4_5	0.508	0.657	0.490	0.519	1.000	0.522	0.318	0.532	0.429	0.501	0.540	0.504	0.526	0.462	0.552	0.454	0.505	0.617	0.545	0.450	0.392	0.440	0.353	0.270	0.386	0.373	0.411	0.534	0.389	0.499	0.407	0.327	0.368	0.366	0.277	0.270	0.456	0.425	0.389	0.288	0.368	0.460	0.510	0.387	0.279	0.368	0.418	0.367	0.368	0.370	0.491	0.550	0.347	0.282	0.085	0.173	0.474
Q4_6	0.473	0.486	0.413	0.489	0.522	1.000	0.570	0.420	0.336	0.468	0.451	0.389	0.317	0.407	0.451	0.461	0.395	0.497	0.446	0.373	0.479	0.441	0.395	0.326	0.458	0.379	0.440	0.494	0.347	0.415	0.426	0.316	0.435	0.364	0.300	0.280	0.350	0.363	0.324	0.276	0.387	0.486	0.496	0.415	0.380	0.418	0.400	0.394	0.370	0.328	0.448	0.497	0.376	0.300	0.225	0.400	0.466
Q4_7	0.316	0.341	0.326	0.430	0.318	0.570	1.000	0.310	0.270	0.412	0.415	0.300	0.150	0.351	0.286	0.352	0.284	0.318	0.368	0.337	0.399	0.311	0.411	0.317	0.342	0.368	0.414	0.355	0.344	0.335	0.396	0.205	0.271	0.231	0.255	0.161	0.294	0.295	0.287	0.238	0.337	0.429	0.342	0.414	0.452	0.400	0.409	0.357	0.425	0.340	0.334	0.312	0.322	0.266	0.199	0.336	0.284
Q4_8	0.585	0.621	0.607	0.610	0.532	0.420	0.310	1.000	0.594	0.574	0.574	0.498	0.486	0.513	0.586	0.470	0.559	0.642	0.619	0.417	0.352	0.400	0.271	0.217	0.360	0.307	0.375	0.433	0.325	0.404	0.354	0.286	0.320	0.352	0.302	0.291	0.409	0.489	0.407	0.310	0.352	0.406	0.415	0.369	0.253	0.296	0.371	0.363	0.269	0.359	0.434	0.487	0.397	0.246	0.082	0.156	0.398
Q4_9	0.431	0.514	0.508	0.498	0.429	0.336	0.270	0.594	1.000	0.467	0.541	0.466	0.456	0.451	0.537	0.421	0.488	0.547	0.706	0.387	0.346	0.370	0.236	0.242	0.366	0.283	0.321	0.330	0.263	0.401	0.399	0.250	0.300	0.245	0.280	0.249	0.332	0.411	0.332	0.331	0.280	0.308	0.379	0.382	0.301	0.326	0.413	0.450	0.347	0.375	0.409	0.457	0.463	0.320	0.129	0.198	0.341
Q4_10	0.568	0.552	0.597	0.645	0.501	0.468	0.412	0.574	0.467	1.000	0.570	0.423	0.342	0.443	0.530	0.493	0.471	0.618	0.553	0.441	0.298	0.299	0.331	0.332	0.381	0.388	0.367	0.469	0.380	0.399	0.373	0.257	0.288	0.333	0.265	0.248	0.383	0.434	0.336	0.311	0.286	0.441	0.419	0.497	0.377	0.393	0.486	0.391	0.395	0.409	0.385	0.432	0.484	0.309	0.158	0.316	0.440
Q4_11	0.586	0.563	0.572	0.573	0.540	0.451	0.415	0.574	0.541	0.570	1.000	0.558	0.473	0.544	0.592	0.558	0.530	0.650	0.677	0.470	0.401	0.406	0.316	0.266	0.428	0.440	0.414	0.528	0.486	0.458	0.395	0.323	0.344	0.324	0.323	0.355	0.428	0.448	0.442	0.383	0.374	0.451	0.526	0.447	0.334	0.392	0.542	0.453	0.347	0.414	0.435	0.481	0.469	0.385	0.204	0.292	0.508
Q4_12	0.408	0.488	0.351	0.439	0.504	0.389	0.300	0.498	0.466	0.423	0.558	1.000	0.694	0.523	0.504	0.420	0.499	0.551	0.541	0.395	0.379	0.430	0.237	0.172	0.314	0.423	0.361	0.421	0.379	0.360	0.350	0.428	0.437	0.423	0.358	0.342	0.499	0.527	0.514	0.402	0.335	0.476	0.450	0.440	0.303	0.357	0.451	0.428	0.310	0.368	0.397	0.397	0.275	0.259	0.103	0.180	0.371
Q4_13	0.408	0.518	0.370	0.381	0.526	0.317	0.150	0.486	0.456	0.342	0.473	0.694	1.000	0.478	0.491	0.367	0.454	0.580	0.501	0.399	0.337	0.404	0.194	0.147	0.278	0.384	0.273	0.397	0.353	0.367	0.334	0.440	0.408	0.388	0.336	0.347	0.476	0.445	0.425	0.329	0.256	0.357	0.413	0.371	0.170	0.224	0.281	0.357	0.202	0.284	0.388	0.455	0.257	0.266	0.074	0.096	0.315
Q4_14	0.543	0.485	0.459	0.489	0.462	0.407	0.351	0.513	0.451	0.443	0.544	0.523	0.478	1.000	0.671	0.586	0.444	0.566	0.521	0.465	0.429	0.461	0.309	0.259	0.460	0.399	0.374	0.502	0.358	0.457	0.419	0.403	0.359	0.344	0.349	0.335	0.422	0.481	0.438	0.442	0.428	0.529	0.478	0.437	0.336	0.332	0.462	0.463	0.371	0.398	0.490	0.421	0.380	0.360	0.217	0.271	0.427
Q4_15	0.533	0.592	0.540	0.524	0.552	0.451	0.286	0.586	0.537	0.530	0.592	0.504	0.491	0.671	1.000	0.701	0.607	0.655	0.593	0.472	0.405	0.455	0.348	0.283	0.486	0.444	0.426	0.529	0.440	0.466	0.454	0.355	0.348	0.338	0.333	0.310	0.430	0.481	0.444	0.381	0.390	0.450	0.503	0.455	0.265	0.332	0.473	0.451	0.331	0.429	0.448	0.492	0.487	0.326	0.137	0.200	0.447
Q4_16	0.540	0.501	0.512	0.526	0.454	0.461	0.352	0.470	0.421	0.493	0.558	0.420	0.367	0.586	0.701	1.000	0.598	0.573	0.532	0.412	0.405	0.466	0.350	0.325	0.488	0.415	0.398	0.495	0.403	0.444	0.426	0.404	0.421	0.364	0.356	0.203	0.377	0.441	0.382	0.276	0.359	0.388	0.467	0.373	0.235	0.291	0.383	0.386	0.260	0.329	0.432	0.440	0.385	0.256	0.102	0.163	0.422
Q4_17	0.469	0.523	0.476	0.507	0.505	0.395	0.284	0.559	0.488	0.471	0.530	0.499	0.454	0.444	0.607	0.598	1.000	0.615	0.535	0.382	0.328	0.373	0.234	0.164	0.367	0.364	0.310	0.348	0.400	0.400	0.336	0.321	0.309	0.352	0.305	0.274	0.421	0.455	0.413	0.296	0.380	0.360	0.376	0.341	0.281	0.360	0.432	0.367	0.333	0.394	0.432	0.452	0.403	0.272	0.097	0.149	0.399
Q4_18	0.655	0.730	0.622	0.663	0.617	0.497	0.318	0.642	0.547	0.618	0.650	0.551	0.580	0.566	0.655	0.573	0.615	1.000	0.659	0.480	0.425	0.419	0.319	0.318	0.515	0.394	0.434	0.530	0.500	0.451	0.426	0.296	0.308	0.323	0.277	0.326	0.389	0.484	0.394	0.332	0.367	0.471	0.496	0.448	0.305	0.386	0.446	0.412	0.352	0.415	0.479	0.550	0.470	0.272	0.096	0.271	0.513
Q4_19	0.495	0.561	0.577	0.530	0.545	0.446	0.368	0.619	0.706	0.553	0.677	0.541	0.501	0.521	0.593	0.532	0.535	0.659	1.000	0.469	0.451	0.471	0.325	0.276	0.477	0.404	0.424	0.521	0.401	0.471	0.445	0.322	0.349	0.326	0.331	0.268	0.423	0.462	0.401	0.388	0.408	0.452	0.495	0.452	0.376	0.387	0.503	0.483	0.429	0.479	0.486	0.507	0.479	0.369	0.130	0.248	0.458
Q5_1	0.422	0.464	0.431	0.419	0.450	0.373	0.337	0.417	0.387	0.441	0.470	0.395	0.399	0.465	0.472	0.412	0.382	0.480	0.469	1.000	0.511	0.574	0.391	0.330	0.494	0.388	0.462	0.551	0.465	0.508	0.466	0.303	0.277	0.242	0.208	0.298	0.349	0.379	0.304	0.362	0.301	0.417	0.536	0.426	0.309	0.329	0.468	0.399	0.363	0.384	0.490	0.423	0.462	0.382	0.156	0.256	0.435
Q5_2	0.337	0.381	0.347	0.368	0.392	0.479	0.399	0.352	0.346	0.298	0.401	0.379	0.337	0.429	0.405	0.405	0.328	0.425	0.451	0.511	1.000	0.650	0.482	0.431	0.610	0.409	0.548	0.469	0.449	0.375	0.513	0.307	0.347	0.316	0.357	0.258	0.326	0.349	0.323	0.258	0.350	0.494	0.472	0.457	0.384	0.397	0.402	0.431	0.442	0.327	0.436	0.416	0.335	0.254	0.154	0.327	0.404
Q5_3	0.362	0.414	0.356	0.348	0.440	0.441	0.311	0.400	0.370	0.299	0.406	0.430	0.404	0.461	0.455	0.466	0.373	0.419	0.471	0.574	0.650	1.000	0.517	0.398	0.610	0.382	0.572	0.575	0.430	0.484	0.491	0.367	0.320	0.298	0.304	0.255	0.362	0.371	0.355	0.314	0.335	0.423	0.521	0.416	0.280	0.300	0.386	0.377	0.324	0.335	0.462	0.421	0.340	0.293	0.122	0.242	0.435
Q5_4	0.349	0.334	0.331	0.383	0.353	0.395	0.411	0.271	0.236	0.331	0.316	0.237	0.194	0.309	0.348	0.350	0.234	0.319	0.325	0.391	0.482	0.517	1.000	0.781	0.586	0.371	0.539	0.433	0.396	0.355	0.440	0.200	0.246	0.253	0.198	0.210	0.268	0.210	0.191	0.174	0.298	0.386	0.414	0.421	0.439	0.308	0.363	0.346	0.469	0.314	0.345	0.322	0.356	0.308	0.145	0.370	0.310
Q5_5	0.283	0.292	0.293	0.365	0.270	0.326	0.317	0.217	0.242	0.332	0.266	0.172	0.147	0.259	0.283	0.325	0.164	0.318	0.276	0.330	0.431	0.398	0.781	1.000	0.587	0.353	0.534	0.395	0.307	0.348	0.387	0.116	0.176	0.193	0.165	0.186	0.185	0.158	0.119	0.110	0.225	0.272	0.356	0.413	0.359	0.304	0.302	0.292	0.389	0.315	0.284	0.260	0.365	0.333	0.150	0.348	0.266
Q5_6	0.394	0.413	0.429	0.473	0.386	0.458	0.342	0.360	0.366	0.381	0.428	0.314	0.278	0.460	0.486	0.488	0.367	0.515	0.477	0.494	0.610	0.610	0.586	0.587	1.000	0.530	0.668	0.572	0.460	0.426	0.522	0.247	0.325	0.337	0.294	0.296	0.334	0.409	0.350	0.250	0.397	0.461	0.488	0.444	0.402	0.407	0.470	0.446	0.422	0.395	0.454	0.453	0.426	0.348	0.140	0.372	0.404
Q5_7	0.298	0.307	0.308	0.406	0.373	0.379	0.368	0.307	0.283	0.388	0.440	0.423	0.384	0.399	0.444	0.415	0.364	0.394	0.404	0.388	0.409	0.382	0.371	0.353	0.530	1.000	0.538	0.571	0.525	0.412	0.445	0.346	0.437	0.436	0.344	0.317	0.442	0.511	0.460	0.405	0.356	0.492	0.464	0.497	0.340	0.360	0.431	0.415	0.311	0.429	0.369	0.372	0.403	0.298	0.135	0.211	0.331
Q5_8	0.319	0.369	0.350	0.387	0.411	0.440	0.414	0.375	0.321	0.367	0.414	0.361	0.273	0.374	0.426	0.398	0.310	0.434	0.424	0.462	0.548	0.572	0.539	0.534	0.668	0.538	1.000	0.637	0.482	0.469	0.497	0.267	0.335	0.366	0.289	0.348	0.335	0.358	0.351	0.251	0.382	0.497	0.506	0.458	0.416	0.426	0.438	0.444	0.386	0.424	0.434	0.422	0.421	0.360	0.152	0.323	0.380
Q5_9	0.432	0.446	0.448	0.429	0.534	0.494	0.355	0.433	0.330	0.469	0.528	0.421	0.397	0.502	0.529	0.495	0.348	0.530	0.521	0.551	0.469	0.575	0.433	0.395	0.572	0.571	0.637	1.000	0.553	0.544	0.519	0.411	0.432	0.442	0.340	0.330	0.448	0.483	0.447	0.363	0.449	0.564	0.587	0.461	0.347	0.435	0.450	0.399	0.307	0.421	0.521	0.500	0.433	0.342	0.103	0.265	0.506
Q5_10	0.350	0.378	0.335	0.409	0.389	0.347	0.344	0.325	0.263	0.380	0.486	0.379	0.353	0.358	0.440	0.403	0.400	0.500	0.401	0.465	0.449	0.430	0.396	0.307	0.460	0.525	0.482	0.553	1.000	0.425	0.435	0.264	0.280	0.333	0.301	0.221	0.420	0.384	0.388	0.261	0.364	0.429	0.436	0.426	0.289	0.363	0.422	0.396	0.335	0.416	0.398	0.417	0.414	0.298	0.040	0.280	0.344
Q5_11	0.424	0.472	0.480	0.384	0.499	0.415	0.335	0.404	0.401	0.399	0.458	0.360	0.367	0.457	0.466	0.444	0.400	0.451	0.471	0.508	0.375	0.484	0.355	0.348	0.426	0.412	0.469	0.544	0.425	1.000	0.495	0.329	0.376	0.335	0.303	0.369	0.376	0.406	0.370	0.339	0.423	0.415	0.576	0.433	0.383	0.446	0.454	0.394	0.354	0.371	0.526	0.472	0.450	0.454	0.317	0.279	0.422
Q5_12	0.330	0.368	0.292	0.437	0.407	0.426	0.396	0.354	0.399	0.373	0.395	0.350	0.334	0.419	0.454	0.426	0.336	0.426	0.445	0.466	0.513	0.491	0.440	0.387	0.522	0.445	0.497	0.519	0.435	0.495	1.000	0.275	0.423	0.348	0.284	0.285	0.378	0.405	0.346	0.265	0.371	0.483	0.481	0.398	0.412	0.485	0.482	0.396	0.410	0.453	0.486	0.455	0.432	0.396	0.200	0.354	0.447
Q6_1	0.293	0.265	0.302	0.234	0.327	0.316	0.205	0.286	0.250	0.257	0.323	0.428	0.440	0.403	0.355	0.404	0.321	0.296	0.322	0.303	0.307	0.367	0.200	0.116	0.247	0.346	0.267	0.411	0.264	0.329	0.275	1.000	0.695	0.652	0.573	0.286	0.577	0.559	0.566	0.280	0.286	0.369	0.472	0.300	0.117	0.220	0.278	0.289	0.143	0.185	0.378	0.389	0.237	0.256	0.124	0.080	0.364
Q6_2	0.275	0.315	0.270	0.306	0.368	0.435	0.271	0.320	0.300	0.288	0.344	0.437	0.408	0.359	0.348	0.421	0.309	0.308	0.349	0.277	0.347	0.320	0.246	0.176	0.325	0.437	0.335	0.432	0.280	0.376	0.423	0.695	1.000	0.725	0.723	0.347	0.595	0.593	0.631	0.253	0.312	0.418	0.461	0.345	0.237	0.322	0.344	0.353	0.152	0.217	0.399	0.435	0.286	0.242	0.095	0.150	0.344
Q6_3	0.235	0.271	0.247	0.299	0.366	0.364	0.231	0.352	0.245	0.333	0.324	0.423	0.388	0.344	0.338	0.364	0.352	0.323	0.326	0.242	0.316	0.298	0.253	0.193	0.337	0.436	0.366	0.442	0.333	0.335	0.348	0.652	0.725	1.000	0.652	0.372	0.638	0.668	0.574	0.227	0.269	0.415	0.447	0.313	0.271	0.295	0.294	0.333	0.179	0.214	0.337	0.404	0.249	0.217	0.095	0.164	0.346
Q6_4	0.257	0.243	0.244	0.226	0.277	0.300	0.255	0.302	0.280	0.265	0.323	0.358	0.336	0.349	0.333	0.356	0.305	0.277	0.331	0.208	0.357	0.304	0.198	0.165	0.294	0.344	0.289	0.340	0.301	0.303	0.284	0.573	0.723	0.652	1.000	0.250	0.560	0.592	0.640	0.191	0.299	0.366	0.357	0.315	0.189	0.320	0.265	0.329	0.142	0.217	0.328	0.394	0.304	0.162	0.022	0.096	0.278
Q6_5	0.250	0.340	0.296	0.281	0.270	0.280	0.161	0.291	0.249	0.248	0.355	0.342	0.347	0.335	0.310	0.203	0.274	0.326	0.268	0.298	0.258	0.255	0.210	0.186	0.296	0.317	0.348	0.330	0.221	0.369	0.285	0.286	0.347	0.372	0.250	1.000	0.406	0.435	0.397	0.329	0.421	0.349	0.377	0.354	0.210	0.243	0.295	0.295	0.234	0.275	0.372	0.410	0.337	0.322	0.211	0.153	0.345
Q6_6	0.290	0.390	0.302	0.408	0.456	0.350	0.294	0.409	0.332	0.383	0.428	0.499	0.476	0.422	0.430	0.377	0.421	0.389	0.423	0.349	0.326	0.362	0.268	0.185	0.334	0.442	0.335	0.448	0.420	0.376	0.378	0.577	0.595	0.638	0.560	0.406	1.000	0.682	0.690	0.346	0.395	0.534	0.519	0.440	0.249	0.389	0.406	0.387	0.209	0.382	0.440	0.534	0.413	0.235	0.060	0.104	0.445
Q6_7	0.369	0.392	0.367	0.394	0.425	0.363	0.295	0.489	0.411	0.434	0.448	0.527	0.445	0.481	0.481	0.441	0.455	0.484	0.462	0.379	0.349	0.371	0.210	0.158	0.409	0.511	0.358	0.483	0.384	0.406	0.405	0.559	0.593	0.668	0.592	0.435	0.682	1.000	0.727	0.401	0.444	0.558	0.514	0.450	0.302	0.383	0.437	0.409	0.274	0.394	0.447	0.503	0.414	0.271	0.075	0.151	0.444
Q6_8	0.312	0.300	0.309	0.354	0.389	0.324	0.287	0.407	0.332	0.336	0.442	0.514	0.425	0.438	0.444	0.382	0.413	0.394	0.401	0.304	0.323	0.355	0.191	0.119	0.350	0.460	0.351	0.447	0.388	0.370	0.346	0.566	0.631	0.574	0.640	0.397	0.690	0.727	1.000	0.403	0.416	0.499	0.477	0.401	0.235	0.425	0.424	0.421	0.196	0.347	0.436	0.486	0.405	0.250	0.057	0.108	0.457
Q6_9	0.245	0.266	0.245	0.290	0.288	0.276	0.238	0.310	0.331	0.311	0.383	0.402	0.329	0.442	0.381	0.276	0.296	0.332	0.388	0.362	0.258	0.314	0.174	0.110	0.250	0.405	0.251	0.363	0.261	0.339	0.265	0.280	0.253	0.227	0.191	0.329	0.346	0.401	0.403	1.000	0.472	0.469	0.387	0.355	0.340	0.273	0.432	0.451	0.335	0.365	0.335	0.342	0.306	0.359	0.352	0.239	0.336
Q6_10	0.309	0.365	0.284	0.364	0.368	0.387	0.337	0.352	0.280	0.286	0.374	0.335	0.256	0.428	0.390	0.359	0.380	0.367	0.408	0.301	0.350	0.335	0.298	0.225	0.397	0.356	0.382	0.449	0.364	0.423	0.371	0.286	0.312	0.269	0.299	0.421	0.395	0.444	0.416	0.472	1.000	0.577	0.431	0.378	0.300	0.325	0.422	0.402	0.360	0.390	0.455	0.419	0.397	0.388	0.198	0.263	0.428
Q6_11	0.357	0.422	0.369	0.460	0.460	0.486	0.429	0.406	0.308	0.441	0.451	0.476	0.357	0.529	0.450	0.388	0.360	0.471	0.452	0.417	0.494	0.423	0.386	0.272	0.461	0.492	0.497	0.564	0.429	0.415	0.483	0.369	0.418	0.415	0.366	0.349	0.534	0.558	0.499	0.469	0.577	1.000	0.568	0.505	0.486	0.471	0.523	0.493	0.469	0.441	0.484	0.477	0.396	0.366	0.218	0.378	0.467
Q7_1	0.458	0.483	0.449	0.469	0.510	0.496	0.342	0.415	0.379	0.419	0.526	0.450	0.413	0.478	0.503	0.467	0.376	0.496	0.495	0.536	0.472	0.521	0.414	0.356	0.488	0.464	0.506	0.587	0.436	0.576	0.481	0.472	0.461	0.447	0.357	0.377	0.519	0.514	0.477	0.387	0.431	0.568	1.000	0.637	0.447	0.530	0.558	0.521	0.408	0.454	0.631	0.640	0.533	0.447	0.195	0.269	0.632
Q7_2	0.340	0.387	0.356	0.476	0.387	0.415	0.414	0.369	0.382	0.497	0.447	0.440	0.371	0.437	0.455	0.373	0.341	0.448	0.452	0.426	0.457	0.416	0.421	0.413	0.444	0.497	0.458	0.461	0.426	0.433	0.398	0.300	0.345	0.313	0.315	0.354	0.440	0.450	0.401	0.355	0.378	0.505	0.637	1.000	0.502	0.572	0.566	0.517	0.464	0.514	0.483	0.492	0.604	0.378	0.218	0.368	0.503
Q7_3	0.247	0.285	0.289	0.370	0.279	0.380	0.452	0.253	0.301	0.377	0.334	0.303	0.170	0.336	0.265	0.235	0.281	0.305	0.376	0.309	0.384	0.280	0.439	0.359	0.402	0.340	0.416	0.347	0.289	0.383	0.412	0.117	0.237	0.271	0.189	0.210	0.249	0.302	0.235	0.340	0.300	0.486	0.447	0.502	1.000	0.565	0.545	0.540	0.732	0.465	0.308	0.290	0.410	0.457	0.324	0.485	0.333
Q7_4	0.331	0.342	0.303	0.487	0.368	0.418	0.400	0.296	0.326	0.393	0.392	0.357	0.224	0.332	0.332	0.291	0.360	0.386	0.387	0.329	0.397	0.300	0.308	0.304	0.407	0.360	0.426	0.435	0.363	0.446	0.485	0.220	0.322	0.295	0.320	0.243	0.389	0.383	0.425	0.273	0.325	0.471	0.530	0.572	0.565	1.000	0.670	0.525	0.446	0.507	0.508	0.464	0.512	0.373	0.155	0.360	0.505
Q7_5	0.398	0.474	0.406	0.499	0.418	0.400	0.409	0.371	0.413	0.486	0.542	0.451	0.281	0.462	0.473	0.383	0.432	0.446	0.503	0.468	0.402	0.386	0.363	0.302	0.470	0.431	0.438	0.450	0.422	0.454	0.482	0.278	0.344	0.294	0.265	0.295	0.406	0.437	0.424	0.432	0.422	0.523	0.558	0.566	0.545	0.670	1.000	0.597	0.569	0.604	0.556	0.555	0.578	0.467	0.299	0.412	0.506
Q7_6	0.357	0.384	0.390	0.473	0.367	0.394	0.357	0.363	0.450	0.391	0.453	0.428	0.357	0.463	0.451	0.386	0.367	0.412	0.483	0.399	0.431	0.377	0.346	0.292	0.446	0.415	0.444	0.399	0.396	0.394	0.396	0.289	0.353	0.333	0.329	0.295	0.387	0.409	0.421	0.451	0.402	0.493	0.521	0.517	0.540	0.525	0.597	1.000	0.562	0.546	0.467	0.476	0.508	0.473	0.234	0.487	0.368
Q7_7	0.287	0.352	0.377	0.403	0.368	0.370	0.425	0.269	0.347	0.395	0.347	0.310	0.202	0.371	0.331	0.260	0.333	0.352	0.429	0.363	0.442	0.324	0.469	0.389	0.422	0.311	0.386	0.307	0.335	0.354	0.410	0.143	0.152	0.179	0.142	0.234	0.209	0.274	0.196	0.335	0.360	0.469	0.408	0.464	0.732	0.446	0.569	0.562	1.000	0.597	0.385	0.332	0.459	0.503	0.378	0.530	0.287
Q7_8	0.298	0.394	0.337	0.436	0.370	0.328	0.340	0.359	0.375	0.409	0.414	0.368	0.284	0.398	0.429	0.329	0.394	0.415	0.479	0.384	0.327	0.335	0.314	0.315	0.395	0.429	0.424	0.421	0.416	0.371	0.453	0.185	0.217	0.214	0.217	0.275	0.382	0.394	0.347	0.365	0.390	0.441	0.454	0.514	0.465	0.507	0.604	0.546	0.597	1.000	0.515	0.465	0.620	0.391	0.255	0.393	0.389
Q7_9	0.527	0.471	0.488	0.521	0.491	0.448	0.334	0.434	0.409	0.385	0.435	0.397	0.388	0.490	0.448	0.432	0.432	0.479	0.486	0.490	0.436	0.462	0.345	0.284	0.454	0.369	0.434	0.521	0.398	0.526	0.486	0.378	0.399	0.337	0.328	0.372	0.440	0.447	0.436	0.335	0.455	0.484	0.631	0.483	0.308	0.508	0.556	0.467	0.385	0.515	1.000	0.693	0.567	0.375	0.188	0.277	0.593
Q7_10	0.495	0.505	0.479	0.516	0.550	0.497	0.312	0.487	0.457	0.432	0.481	0.397	0.455	0.421	0.492	0.440	0.452	0.550	0.507	0.423	0.416	0.421	0.322	0.260	0.453	0.372	0.422	0.500	0.417	0.472	0.455	0.389	0.435	0.404	0.394	0.410	0.534	0.503	0.486	0.342	0.419	0.477	0.640	0.492	0.290	0.464	0.555	0.476	0.332	0.465	0.693	1.000	0.538	0.323	0.127	0.190	0.680
Q7_11	0.423	0.407	0.472	0.517	0.347	0.376	0.322	0.397	0.463	0.484	0.469	0.275	0.257	0.380	0.487	0.385	0.403	0.470	0.479	0.462	0.335	0.340	0.356	0.365	0.426	0.403	0.421	0.433	0.414	0.450	0.432	0.237	0.286	0.249	0.304	0.337	0.413	0.414	0.405	0.306	0.397	0.396	0.533	0.604	0.410	0.512	0.578	0.508	0.459	0.620	0.567	0.538	1.000	0.519	0.260	0.344	0.446
Q7_12	0.307	0.281	0.345	0.334	0.282	0.300	0.266	0.246	0.320	0.309	0.385	0.259	0.266	0.360	0.326	0.256	0.272	0.272	0.369	0.382	0.254	0.293	0.308	0.333	0.348	0.298	0.360	0.342	0.298	0.454	0.396	0.256	0.242	0.217	0.162	0.322	0.235	0.271	0.250	0.359	0.388	0.366	0.447	0.378	0.457	0.373	0.467	0.473	0.503	0.391	0.375	0.323	0.519	1.000	0.483	0.449	0.366
Q7_13	0.127	0.129	0.148	0.134	0.085	0.225	0.199	0.082	0.129	0.158	0.204	0.103	0.074	0.217	0.137	0.102	0.097	0.096	0.130	0.156	0.154	0.122	0.145	0.150	0.140	0.135	0.152	0.103	0.040	0.317	0.200	0.124	0.095	0.095	0.022	0.211	0.060	0.075	0.057	0.352	0.198	0.218	0.195	0.218	0.324	0.155	0.299	0.234	0.378	0.255	0.188	0.127	0.260	0.483	1.000	0.424	0.138
Q7_14	0.218	0.197	0.211	0.308	0.173	0.400	0.336	0.156	0.198	0.316	0.292	0.180	0.096	0.271	0.200	0.163	0.149	0.271	0.248	0.256	0.327	0.242	0.370	0.348	0.372	0.211	0.323	0.265	0.280	0.279	0.354	0.080	0.150	0.164	0.096	0.153	0.104	0.151	0.108	0.239	0.263	0.378	0.269	0.368	0.485	0.360	0.412	0.487	0.530	0.393	0.277	0.190	0.344	0.449	0.424	1.000	0.285
Q7_15	0.445	0.454	0.411	0.477	0.474	0.466	0.284	0.398	0.341	0.440	0.508	0.371	0.315	0.427	0.447	0.422	0.399	0.513	0.458	0.435	0.404	0.435	0.310	0.266	0.404	0.331	0.380	0.506	0.344	0.422	0.447	0.364	0.344	0.346	0.278	0.345	0.445	0.444	0.457	0.336	0.428	0.467	0.632	0.503	0.333	0.505	0.506	0.368	0.287	0.389	0.593	0.680	0.446	0.366	0.138	0.285	1.000

# Polychoric Correlation
corr.pc <- polychoric(dat)

Warning in cor.smooth(mat): Matrix was not positive definite, smoothing was done

kable(corr.pc$rho,digits=3,format = "html")%>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%", height="500px")

	Q4_1	Q4_2	Q4_3	Q4_4	Q4_5	Q4_6	Q4_7	Q4_8	Q4_9	Q4_10	Q4_11	Q4_12	Q4_13	Q4_14	Q4_15	Q4_16	Q4_17	Q4_18	Q4_19	Q5_1	Q5_2	Q5_3	Q5_4	Q5_5	Q5_6	Q5_7	Q5_8	Q5_9	Q5_10	Q5_11	Q5_12	Q6_1	Q6_2	Q6_3	Q6_4	Q6_5	Q6_6	Q6_7	Q6_8	Q6_9	Q6_10	Q6_11	Q7_1	Q7_2	Q7_3	Q7_4	Q7_5	Q7_6	Q7_7	Q7_8	Q7_9	Q7_10	Q7_11	Q7_12	Q7_13	Q7_14	Q7_15
Q4_1	1.000	0.701	0.761	0.752	0.574	0.522	0.349	0.655	0.491	0.643	0.648	0.471	0.500	0.607	0.602	0.606	0.533	0.734	0.558	0.474	0.377	0.407	0.381	0.319	0.438	0.340	0.347	0.487	0.404	0.476	0.364	0.370	0.325	0.304	0.307	0.300	0.356	0.434	0.370	0.288	0.345	0.404	0.516	0.390	0.266	0.369	0.444	0.406	0.334	0.332	0.586	0.570	0.484	0.351	0.134	0.229	0.502
Q4_2	0.701	1.000	0.721	0.717	0.731	0.551	0.380	0.693	0.576	0.629	0.632	0.557	0.615	0.534	0.663	0.565	0.591	0.804	0.624	0.530	0.434	0.472	0.384	0.338	0.479	0.351	0.423	0.512	0.455	0.532	0.421	0.351	0.372	0.337	0.285	0.400	0.475	0.468	0.359	0.318	0.410	0.483	0.557	0.453	0.315	0.388	0.546	0.442	0.411	0.449	0.537	0.591	0.482	0.314	0.137	0.217	0.522
Q4_3	0.761	0.721	1.000	0.766	0.550	0.463	0.347	0.681	0.579	0.676	0.632	0.409	0.451	0.502	0.603	0.571	0.542	0.694	0.640	0.485	0.387	0.400	0.357	0.328	0.488	0.348	0.388	0.505	0.385	0.538	0.323	0.393	0.313	0.317	0.284	0.360	0.363	0.432	0.357	0.290	0.319	0.415	0.504	0.398	0.308	0.338	0.454	0.443	0.411	0.379	0.546	0.549	0.535	0.374	0.154	0.230	0.463
Q4_4	0.752	0.717	0.766	1.000	0.590	0.544	0.469	0.690	0.572	0.735	0.642	0.521	0.467	0.537	0.589	0.592	0.591	0.749	0.594	0.474	0.401	0.399	0.414	0.399	0.523	0.446	0.422	0.485	0.462	0.433	0.481	0.305	0.365	0.384	0.274	0.346	0.514	0.465	0.416	0.345	0.399	0.506	0.536	0.532	0.386	0.543	0.552	0.527	0.431	0.474	0.579	0.597	0.592	0.351	0.142	0.313	0.539
Q4_5	0.574	0.731	0.550	0.590	1.000	0.581	0.357	0.590	0.474	0.576	0.602	0.576	0.635	0.521	0.618	0.516	0.570	0.685	0.610	0.507	0.444	0.492	0.412	0.318	0.440	0.421	0.466	0.600	0.461	0.558	0.465	0.400	0.426	0.440	0.329	0.322	0.536	0.501	0.451	0.338	0.419	0.518	0.578	0.446	0.318	0.420	0.474	0.424	0.419	0.424	0.559	0.621	0.409	0.315	0.078	0.172	0.543
Q4_6	0.522	0.551	0.463	0.544	0.581	1.000	0.640	0.477	0.377	0.529	0.498	0.442	0.396	0.451	0.502	0.516	0.448	0.563	0.500	0.413	0.523	0.486	0.431	0.359	0.501	0.419	0.477	0.545	0.383	0.457	0.466	0.376	0.490	0.425	0.338	0.314	0.413	0.417	0.369	0.313	0.432	0.529	0.552	0.466	0.413	0.456	0.434	0.432	0.435	0.360	0.497	0.563	0.426	0.329	0.251	0.431	0.523
Q4_7	0.349	0.380	0.347	0.469	0.357	0.640	1.000	0.334	0.289	0.442	0.460	0.349	0.176	0.397	0.319	0.399	0.325	0.351	0.405	0.373	0.423	0.341	0.431	0.326	0.385	0.434	0.448	0.405	0.385	0.377	0.431	0.253	0.321	0.284	0.300	0.186	0.360	0.338	0.343	0.279	0.376	0.473	0.389	0.464	0.482	0.439	0.444	0.383	0.461	0.358	0.369	0.363	0.363	0.278	0.217	0.337	0.332
Q4_8	0.655	0.693	0.681	0.690	0.590	0.477	0.334	1.000	0.652	0.654	0.636	0.565	0.583	0.572	0.650	0.529	0.627	0.719	0.693	0.467	0.398	0.452	0.301	0.247	0.408	0.351	0.423	0.486	0.382	0.450	0.399	0.355	0.366	0.425	0.347	0.343	0.481	0.556	0.461	0.361	0.399	0.463	0.476	0.429	0.281	0.333	0.420	0.419	0.316	0.411	0.490	0.552	0.461	0.271	0.085	0.166	0.446
Q4_9	0.491	0.576	0.579	0.572	0.474	0.377	0.289	0.652	1.000	0.540	0.594	0.519	0.548	0.502	0.600	0.475	0.543	0.613	0.766	0.438	0.390	0.413	0.267	0.284	0.414	0.329	0.359	0.382	0.316	0.451	0.450	0.328	0.336	0.324	0.319	0.305	0.394	0.474	0.384	0.375	0.308	0.350	0.439	0.451	0.332	0.370	0.470	0.506	0.392	0.422	0.467	0.519	0.534	0.360	0.135	0.213	0.384
Q4_10	0.643	0.629	0.676	0.735	0.576	0.529	0.442	0.654	0.540	1.000	0.642	0.519	0.456	0.497	0.611	0.568	0.552	0.721	0.640	0.507	0.324	0.361	0.375	0.376	0.436	0.442	0.418	0.538	0.446	0.459	0.426	0.341	0.360	0.436	0.332	0.322	0.486	0.540	0.418	0.378	0.334	0.502	0.485	0.572	0.419	0.440	0.545	0.449	0.441	0.458	0.442	0.521	0.559	0.333	0.176	0.338	0.506
Q4_11	0.648	0.632	0.632	0.642	0.602	0.498	0.460	0.636	0.594	0.642	1.000	0.634	0.588	0.600	0.653	0.619	0.595	0.724	0.738	0.522	0.441	0.454	0.353	0.302	0.473	0.491	0.457	0.585	0.550	0.512	0.437	0.400	0.397	0.396	0.370	0.414	0.500	0.520	0.510	0.437	0.413	0.504	0.589	0.511	0.367	0.435	0.599	0.512	0.399	0.459	0.485	0.539	0.544	0.432	0.226	0.312	0.566
Q4_12	0.471	0.557	0.409	0.521	0.576	0.442	0.349	0.565	0.519	0.519	0.634	1.000	0.814	0.608	0.568	0.490	0.562	0.632	0.603	0.454	0.434	0.481	0.290	0.213	0.370	0.491	0.415	0.489	0.463	0.411	0.404	0.520	0.505	0.517	0.416	0.421	0.599	0.610	0.600	0.467	0.392	0.551	0.520	0.525	0.365	0.408	0.521	0.485	0.375	0.421	0.458	0.454	0.342	0.304	0.110	0.193	0.428
Q4_13	0.500	0.615	0.451	0.467	0.635	0.396	0.176	0.583	0.548	0.456	0.588	0.814	1.000	0.611	0.577	0.458	0.521	0.698	0.619	0.514	0.446	0.503	0.236	0.179	0.361	0.476	0.356	0.496	0.463	0.452	0.427	0.561	0.506	0.490	0.427	0.463	0.575	0.574	0.521	0.445	0.315	0.452	0.529	0.485	0.226	0.288	0.385	0.471	0.258	0.359	0.488	0.558	0.352	0.345	0.062	0.083	0.398
Q4_14	0.607	0.534	0.502	0.537	0.521	0.451	0.397	0.572	0.502	0.497	0.600	0.608	0.611	1.000	0.742	0.655	0.502	0.633	0.580	0.519	0.469	0.519	0.343	0.284	0.509	0.445	0.417	0.560	0.406	0.516	0.451	0.505	0.430	0.431	0.411	0.401	0.501	0.567	0.518	0.508	0.486	0.576	0.535	0.484	0.364	0.365	0.507	0.519	0.424	0.431	0.546	0.491	0.433	0.411	0.240	0.278	0.487
Q4_15	0.602	0.663	0.603	0.589	0.618	0.502	0.319	0.650	0.600	0.611	0.653	0.568	0.577	0.742	1.000	0.774	0.671	0.735	0.659	0.526	0.451	0.514	0.401	0.320	0.551	0.500	0.478	0.593	0.505	0.517	0.504	0.421	0.408	0.416	0.384	0.364	0.508	0.557	0.507	0.432	0.435	0.503	0.566	0.521	0.294	0.373	0.532	0.519	0.384	0.484	0.503	0.553	0.557	0.370	0.145	0.207	0.501
Q4_16	0.606	0.565	0.571	0.592	0.516	0.516	0.399	0.529	0.475	0.568	0.619	0.490	0.458	0.655	0.774	1.000	0.669	0.646	0.594	0.461	0.445	0.524	0.388	0.356	0.554	0.468	0.443	0.557	0.463	0.497	0.473	0.499	0.492	0.448	0.417	0.246	0.462	0.513	0.447	0.325	0.408	0.437	0.524	0.426	0.253	0.328	0.431	0.437	0.288	0.364	0.486	0.506	0.438	0.291	0.106	0.160	0.483
Q4_17	0.533	0.591	0.542	0.591	0.570	0.448	0.325	0.627	0.543	0.552	0.595	0.562	0.521	0.502	0.671	0.669	1.000	0.691	0.601	0.440	0.381	0.421	0.267	0.190	0.421	0.418	0.355	0.404	0.469	0.451	0.382	0.394	0.350	0.427	0.354	0.313	0.498	0.525	0.469	0.344	0.436	0.408	0.431	0.397	0.318	0.407	0.490	0.420	0.382	0.450	0.491	0.512	0.470	0.301	0.090	0.160	0.455
Q4_18	0.734	0.804	0.694	0.749	0.685	0.563	0.351	0.719	0.613	0.721	0.724	0.632	0.698	0.633	0.735	0.646	0.691	1.000	0.731	0.547	0.483	0.479	0.365	0.369	0.585	0.452	0.495	0.605	0.587	0.505	0.480	0.380	0.361	0.406	0.325	0.377	0.472	0.566	0.454	0.390	0.420	0.535	0.569	0.520	0.336	0.440	0.506	0.469	0.406	0.465	0.541	0.626	0.562	0.312	0.096	0.295	0.584
Q4_19	0.558	0.624	0.640	0.594	0.610	0.500	0.405	0.693	0.766	0.640	0.738	0.603	0.619	0.580	0.659	0.594	0.601	0.731	1.000	0.528	0.501	0.522	0.357	0.307	0.530	0.461	0.468	0.586	0.462	0.522	0.494	0.417	0.404	0.416	0.391	0.328	0.505	0.541	0.466	0.449	0.456	0.505	0.561	0.507	0.422	0.431	0.553	0.537	0.490	0.542	0.547	0.569	0.553	0.419	0.134	0.266	0.515
Q5_1	0.474	0.530	0.485	0.474	0.507	0.413	0.373	0.467	0.438	0.507	0.522	0.454	0.514	0.519	0.526	0.461	0.440	0.547	0.528	1.000	0.555	0.631	0.438	0.366	0.550	0.432	0.514	0.608	0.530	0.562	0.517	0.381	0.315	0.291	0.235	0.360	0.424	0.432	0.352	0.418	0.330	0.465	0.593	0.474	0.334	0.361	0.515	0.441	0.407	0.419	0.542	0.474	0.530	0.423	0.167	0.270	0.487
Q5_2	0.377	0.434	0.387	0.401	0.444	0.523	0.423	0.398	0.390	0.324	0.441	0.434	0.446	0.469	0.451	0.445	0.381	0.483	0.501	0.555	1.000	0.707	0.503	0.447	0.659	0.443	0.578	0.515	0.485	0.411	0.544	0.379	0.391	0.383	0.404	0.311	0.396	0.403	0.377	0.300	0.377	0.533	0.511	0.484	0.384	0.419	0.432	0.459	0.484	0.341	0.475	0.474	0.359	0.258	0.164	0.327	0.444
Q5_3	0.407	0.472	0.400	0.399	0.492	0.486	0.341	0.452	0.413	0.361	0.454	0.481	0.503	0.519	0.514	0.524	0.421	0.479	0.522	0.631	0.707	1.000	0.569	0.441	0.671	0.427	0.625	0.631	0.487	0.536	0.538	0.453	0.369	0.357	0.345	0.298	0.427	0.424	0.410	0.365	0.373	0.469	0.576	0.471	0.300	0.332	0.429	0.423	0.369	0.374	0.512	0.475	0.388	0.316	0.129	0.246	0.486
Q5_4	0.381	0.384	0.357	0.414	0.412	0.431	0.431	0.301	0.267	0.375	0.353	0.290	0.236	0.343	0.401	0.388	0.267	0.365	0.357	0.438	0.503	0.569	1.000	0.837	0.632	0.390	0.585	0.488	0.433	0.417	0.486	0.221	0.267	0.290	0.205	0.243	0.302	0.227	0.210	0.223	0.320	0.415	0.451	0.444	0.478	0.324	0.389	0.380	0.532	0.364	0.371	0.367	0.373	0.341	0.168	0.379	0.344
Q5_5	0.319	0.338	0.328	0.399	0.318	0.359	0.326	0.247	0.284	0.376	0.302	0.213	0.179	0.284	0.320	0.356	0.190	0.369	0.307	0.366	0.447	0.441	0.837	1.000	0.628	0.367	0.577	0.446	0.343	0.408	0.433	0.141	0.208	0.228	0.180	0.226	0.205	0.180	0.140	0.153	0.237	0.289	0.394	0.434	0.389	0.315	0.316	0.323	0.429	0.349	0.313	0.311	0.373	0.355	0.174	0.363	0.300
Q5_6	0.438	0.479	0.488	0.523	0.440	0.501	0.385	0.408	0.414	0.436	0.473	0.370	0.361	0.509	0.551	0.554	0.421	0.585	0.530	0.550	0.659	0.671	0.632	0.628	1.000	0.561	0.717	0.632	0.488	0.487	0.570	0.305	0.373	0.400	0.331	0.352	0.386	0.464	0.408	0.289	0.442	0.495	0.538	0.463	0.423	0.435	0.510	0.488	0.470	0.426	0.506	0.519	0.481	0.374	0.150	0.376	0.452
Q5_7	0.340	0.351	0.348	0.446	0.421	0.419	0.434	0.351	0.329	0.442	0.491	0.491	0.476	0.445	0.500	0.468	0.418	0.452	0.461	0.432	0.443	0.427	0.390	0.367	0.561	1.000	0.572	0.627	0.576	0.460	0.475	0.429	0.499	0.520	0.396	0.374	0.514	0.590	0.533	0.467	0.399	0.541	0.520	0.546	0.384	0.394	0.468	0.453	0.341	0.457	0.419	0.420	0.452	0.325	0.151	0.215	0.369
Q5_8	0.347	0.423	0.388	0.422	0.466	0.477	0.448	0.423	0.359	0.418	0.457	0.415	0.356	0.417	0.478	0.443	0.355	0.495	0.468	0.514	0.578	0.625	0.585	0.577	0.717	0.572	1.000	0.693	0.532	0.520	0.534	0.325	0.378	0.429	0.321	0.411	0.392	0.399	0.399	0.291	0.421	0.534	0.553	0.496	0.440	0.460	0.465	0.488	0.426	0.464	0.473	0.472	0.460	0.385	0.169	0.344	0.422
Q5_9	0.487	0.512	0.505	0.485	0.600	0.545	0.405	0.486	0.382	0.538	0.585	0.489	0.496	0.560	0.593	0.557	0.404	0.605	0.586	0.608	0.515	0.631	0.488	0.446	0.632	0.627	0.693	1.000	0.627	0.599	0.568	0.498	0.494	0.511	0.390	0.389	0.519	0.550	0.510	0.421	0.502	0.620	0.645	0.512	0.379	0.478	0.498	0.444	0.344	0.463	0.577	0.557	0.496	0.376	0.103	0.278	0.565
Q5_10	0.404	0.455	0.385	0.462	0.461	0.383	0.385	0.382	0.316	0.446	0.550	0.463	0.463	0.406	0.505	0.463	0.469	0.587	0.462	0.530	0.485	0.487	0.433	0.343	0.488	0.576	0.532	0.627	1.000	0.498	0.470	0.345	0.337	0.423	0.351	0.283	0.525	0.462	0.458	0.328	0.398	0.464	0.500	0.476	0.295	0.405	0.473	0.446	0.386	0.459	0.454	0.498	0.478	0.322	0.039	0.284	0.397
Q5_11	0.476	0.532	0.538	0.433	0.558	0.457	0.377	0.450	0.451	0.459	0.512	0.411	0.452	0.516	0.517	0.497	0.451	0.505	0.522	0.562	0.411	0.536	0.417	0.408	0.487	0.460	0.520	0.599	0.498	1.000	0.549	0.412	0.428	0.384	0.332	0.425	0.440	0.461	0.422	0.380	0.478	0.461	0.637	0.479	0.432	0.491	0.501	0.442	0.423	0.419	0.581	0.528	0.507	0.510	0.353	0.309	0.473
Q5_12	0.364	0.421	0.323	0.481	0.465	0.466	0.431	0.399	0.450	0.426	0.437	0.404	0.427	0.451	0.504	0.473	0.382	0.480	0.494	0.517	0.544	0.538	0.486	0.433	0.570	0.475	0.534	0.568	0.470	0.549	1.000	0.343	0.483	0.411	0.324	0.331	0.453	0.460	0.402	0.314	0.400	0.521	0.536	0.429	0.430	0.520	0.515	0.423	0.441	0.485	0.542	0.521	0.475	0.414	0.217	0.349	0.494
Q6_1	0.370	0.351	0.393	0.305	0.400	0.376	0.253	0.355	0.328	0.341	0.400	0.520	0.561	0.505	0.421	0.499	0.394	0.380	0.417	0.381	0.379	0.453	0.221	0.141	0.305	0.429	0.325	0.498	0.345	0.412	0.343	1.000	0.788	0.753	0.663	0.380	0.675	0.671	0.666	0.352	0.351	0.444	0.572	0.384	0.142	0.277	0.344	0.366	0.166	0.231	0.478	0.470	0.308	0.319	0.134	0.071	0.464
Q6_2	0.325	0.372	0.313	0.365	0.426	0.490	0.321	0.366	0.336	0.360	0.397	0.505	0.506	0.430	0.408	0.492	0.350	0.361	0.404	0.315	0.391	0.369	0.267	0.208	0.373	0.499	0.378	0.494	0.337	0.428	0.483	0.788	1.000	0.803	0.787	0.429	0.671	0.669	0.707	0.298	0.354	0.476	0.523	0.405	0.261	0.361	0.392	0.399	0.159	0.252	0.454	0.486	0.333	0.256	0.081	0.145	0.388
Q6_3	0.304	0.337	0.317	0.384	0.440	0.425	0.284	0.425	0.324	0.436	0.396	0.517	0.490	0.431	0.416	0.448	0.427	0.406	0.416	0.291	0.383	0.357	0.290	0.228	0.400	0.520	0.429	0.511	0.423	0.384	0.411	0.753	0.803	1.000	0.743	0.459	0.737	0.767	0.664	0.295	0.316	0.492	0.535	0.391	0.319	0.349	0.361	0.408	0.212	0.255	0.412	0.481	0.318	0.230	0.073	0.163	0.415
Q6_4	0.307	0.285	0.284	0.274	0.329	0.338	0.300	0.347	0.319	0.332	0.370	0.416	0.427	0.411	0.384	0.417	0.354	0.325	0.391	0.235	0.404	0.345	0.205	0.180	0.331	0.396	0.321	0.390	0.351	0.332	0.324	0.663	0.787	0.743	1.000	0.310	0.638	0.664	0.719	0.226	0.338	0.422	0.403	0.361	0.208	0.360	0.301	0.368	0.140	0.239	0.373	0.448	0.349	0.165	0.003	0.075	0.311
Q6_5	0.300	0.400	0.360	0.346	0.322	0.314	0.186	0.343	0.305	0.322	0.414	0.421	0.463	0.401	0.364	0.246	0.313	0.377	0.328	0.360	0.311	0.298	0.243	0.226	0.352	0.374	0.411	0.389	0.283	0.425	0.331	0.380	0.429	0.459	0.310	1.000	0.486	0.498	0.466	0.386	0.477	0.404	0.455	0.428	0.237	0.291	0.341	0.351	0.262	0.312	0.436	0.472	0.396	0.357	0.213	0.169	0.408
Q6_6	0.356	0.475	0.363	0.514	0.536	0.413	0.360	0.481	0.394	0.486	0.500	0.599	0.575	0.501	0.508	0.462	0.498	0.472	0.505	0.424	0.396	0.427	0.302	0.205	0.386	0.514	0.392	0.519	0.525	0.440	0.453	0.675	0.671	0.737	0.638	0.486	1.000	0.786	0.778	0.429	0.452	0.641	0.609	0.526	0.280	0.465	0.486	0.464	0.226	0.447	0.518	0.613	0.502	0.260	0.041	0.078	0.536
Q6_7	0.434	0.468	0.432	0.465	0.501	0.417	0.338	0.556	0.474	0.540	0.520	0.610	0.574	0.567	0.557	0.513	0.525	0.566	0.541	0.432	0.403	0.424	0.227	0.180	0.464	0.590	0.399	0.550	0.462	0.461	0.460	0.671	0.669	0.767	0.664	0.498	0.786	1.000	0.814	0.468	0.501	0.640	0.589	0.520	0.347	0.439	0.502	0.461	0.311	0.441	0.506	0.572	0.485	0.298	0.062	0.141	0.515
Q6_8	0.370	0.359	0.357	0.416	0.451	0.369	0.343	0.461	0.384	0.418	0.510	0.600	0.521	0.518	0.507	0.447	0.469	0.454	0.466	0.352	0.377	0.410	0.210	0.140	0.408	0.533	0.399	0.510	0.458	0.422	0.402	0.666	0.707	0.664	0.719	0.466	0.778	0.814	1.000	0.469	0.465	0.568	0.544	0.469	0.278	0.488	0.487	0.482	0.215	0.387	0.498	0.538	0.477	0.274	0.048	0.110	0.516
Q6_9	0.288	0.318	0.290	0.345	0.338	0.313	0.279	0.361	0.375	0.378	0.437	0.467	0.445	0.508	0.432	0.325	0.344	0.390	0.449	0.418	0.300	0.365	0.223	0.153	0.289	0.467	0.291	0.421	0.328	0.380	0.314	0.352	0.298	0.295	0.226	0.386	0.429	0.468	0.469	1.000	0.539	0.534	0.454	0.422	0.394	0.323	0.496	0.507	0.402	0.416	0.394	0.402	0.371	0.430	0.389	0.275	0.400
Q6_10	0.345	0.410	0.319	0.399	0.419	0.432	0.376	0.399	0.308	0.334	0.413	0.392	0.315	0.486	0.435	0.408	0.436	0.420	0.456	0.330	0.377	0.373	0.320	0.237	0.442	0.399	0.421	0.502	0.398	0.478	0.400	0.351	0.354	0.316	0.338	0.477	0.452	0.501	0.465	0.539	1.000	0.630	0.482	0.393	0.323	0.350	0.456	0.433	0.429	0.427	0.505	0.481	0.442	0.437	0.231	0.284	0.485
Q6_11	0.404	0.483	0.415	0.506	0.518	0.529	0.473	0.463	0.350	0.502	0.504	0.551	0.452	0.576	0.503	0.437	0.408	0.535	0.505	0.465	0.533	0.469	0.415	0.289	0.495	0.541	0.534	0.620	0.464	0.461	0.521	0.444	0.476	0.492	0.422	0.404	0.641	0.640	0.568	0.534	0.630	1.000	0.627	0.543	0.510	0.501	0.571	0.532	0.508	0.469	0.533	0.539	0.444	0.392	0.240	0.399	0.525
Q7_1	0.516	0.557	0.504	0.536	0.578	0.552	0.389	0.476	0.439	0.485	0.589	0.520	0.529	0.535	0.566	0.524	0.431	0.569	0.561	0.593	0.511	0.576	0.451	0.394	0.538	0.520	0.553	0.645	0.500	0.637	0.536	0.572	0.523	0.535	0.403	0.455	0.609	0.589	0.544	0.454	0.482	0.627	1.000	0.706	0.489	0.582	0.612	0.575	0.445	0.502	0.689	0.722	0.602	0.488	0.214	0.273	0.702
Q7_2	0.390	0.453	0.398	0.532	0.446	0.466	0.464	0.429	0.451	0.572	0.511	0.525	0.485	0.484	0.521	0.426	0.397	0.520	0.507	0.474	0.484	0.471	0.444	0.434	0.463	0.546	0.496	0.512	0.476	0.479	0.429	0.384	0.405	0.391	0.361	0.428	0.526	0.520	0.469	0.422	0.393	0.543	0.706	1.000	0.561	0.617	0.599	0.546	0.508	0.544	0.530	0.568	0.649	0.408	0.247	0.378	0.570
Q7_3	0.266	0.315	0.308	0.386	0.318	0.413	0.482	0.281	0.332	0.419	0.367	0.365	0.226	0.364	0.294	0.253	0.318	0.336	0.422	0.334	0.384	0.300	0.478	0.389	0.423	0.384	0.440	0.379	0.295	0.432	0.430	0.142	0.261	0.319	0.208	0.237	0.280	0.347	0.278	0.394	0.323	0.510	0.489	0.561	1.000	0.609	0.569	0.589	0.803	0.498	0.325	0.328	0.430	0.498	0.351	0.497	0.370
Q7_4	0.369	0.388	0.338	0.543	0.420	0.456	0.439	0.333	0.370	0.440	0.435	0.408	0.288	0.365	0.373	0.328	0.407	0.440	0.431	0.361	0.419	0.332	0.324	0.315	0.435	0.394	0.460	0.478	0.405	0.491	0.520	0.277	0.361	0.349	0.360	0.291	0.465	0.439	0.488	0.323	0.350	0.501	0.582	0.617	0.609	1.000	0.707	0.560	0.483	0.551	0.554	0.527	0.564	0.402	0.171	0.382	0.558
Q7_5	0.444	0.546	0.454	0.552	0.474	0.434	0.444	0.420	0.470	0.545	0.599	0.521	0.385	0.507	0.532	0.431	0.490	0.506	0.553	0.515	0.432	0.429	0.389	0.316	0.510	0.468	0.465	0.498	0.473	0.501	0.515	0.344	0.392	0.361	0.301	0.341	0.486	0.502	0.487	0.496	0.456	0.571	0.612	0.599	0.569	0.707	1.000	0.641	0.635	0.657	0.604	0.620	0.628	0.504	0.342	0.437	0.562
Q7_6	0.406	0.442	0.443	0.527	0.424	0.432	0.383	0.419	0.506	0.449	0.512	0.485	0.471	0.519	0.519	0.437	0.420	0.469	0.537	0.441	0.459	0.423	0.380	0.323	0.488	0.453	0.488	0.444	0.446	0.442	0.423	0.366	0.399	0.408	0.368	0.351	0.464	0.461	0.482	0.507	0.433	0.532	0.575	0.546	0.589	0.560	0.641	1.000	0.620	0.587	0.510	0.546	0.558	0.518	0.267	0.527	0.413
Q7_7	0.334	0.411	0.411	0.431	0.419	0.435	0.461	0.316	0.392	0.441	0.399	0.375	0.258	0.424	0.384	0.288	0.382	0.406	0.490	0.407	0.484	0.369	0.532	0.429	0.470	0.341	0.426	0.344	0.386	0.423	0.441	0.166	0.159	0.212	0.140	0.262	0.226	0.311	0.215	0.402	0.429	0.508	0.445	0.508	0.803	0.483	0.635	0.620	1.000	0.639	0.428	0.381	0.493	0.575	0.446	0.588	0.333
Q7_8	0.332	0.449	0.379	0.474	0.424	0.360	0.358	0.411	0.422	0.458	0.459	0.421	0.359	0.431	0.484	0.364	0.450	0.465	0.542	0.419	0.341	0.374	0.364	0.349	0.426	0.457	0.464	0.463	0.459	0.419	0.485	0.231	0.252	0.255	0.239	0.312	0.447	0.441	0.387	0.416	0.427	0.469	0.502	0.544	0.498	0.551	0.657	0.587	0.639	1.000	0.572	0.532	0.680	0.439	0.293	0.419	0.435
Q7_9	0.586	0.537	0.546	0.579	0.559	0.497	0.369	0.490	0.467	0.442	0.485	0.458	0.488	0.546	0.503	0.486	0.491	0.541	0.547	0.542	0.475	0.512	0.371	0.313	0.506	0.419	0.473	0.577	0.454	0.581	0.542	0.478	0.454	0.412	0.373	0.436	0.518	0.506	0.498	0.394	0.505	0.533	0.689	0.530	0.325	0.554	0.604	0.510	0.428	0.572	1.000	0.762	0.632	0.405	0.204	0.296	0.654
Q7_10	0.570	0.591	0.549	0.597	0.621	0.563	0.363	0.552	0.519	0.521	0.539	0.454	0.558	0.491	0.553	0.506	0.512	0.626	0.569	0.474	0.474	0.475	0.367	0.311	0.519	0.420	0.472	0.557	0.498	0.528	0.521	0.470	0.486	0.481	0.448	0.472	0.613	0.572	0.538	0.402	0.481	0.539	0.722	0.568	0.328	0.527	0.620	0.546	0.381	0.532	0.762	1.000	0.624	0.358	0.132	0.213	0.761
Q7_11	0.484	0.482	0.535	0.592	0.409	0.426	0.363	0.461	0.534	0.559	0.544	0.342	0.352	0.433	0.557	0.438	0.470	0.562	0.553	0.530	0.359	0.388	0.373	0.373	0.481	0.452	0.460	0.496	0.478	0.507	0.475	0.308	0.333	0.318	0.349	0.396	0.502	0.485	0.477	0.371	0.442	0.444	0.602	0.649	0.430	0.564	0.628	0.558	0.493	0.680	0.632	0.624	1.000	0.570	0.294	0.387	0.524
Q7_12	0.351	0.314	0.374	0.351	0.315	0.329	0.278	0.271	0.360	0.333	0.432	0.304	0.345	0.411	0.370	0.291	0.301	0.312	0.419	0.423	0.258	0.316	0.341	0.355	0.374	0.325	0.385	0.376	0.322	0.510	0.414	0.319	0.256	0.230	0.165	0.357	0.260	0.298	0.274	0.430	0.437	0.392	0.488	0.408	0.498	0.402	0.504	0.518	0.575	0.439	0.405	0.358	0.570	1.000	0.559	0.492	0.397
Q7_13	0.134	0.137	0.154	0.142	0.078	0.251	0.217	0.085	0.135	0.176	0.226	0.110	0.062	0.240	0.145	0.106	0.090	0.096	0.134	0.167	0.164	0.129	0.168	0.174	0.150	0.151	0.169	0.103	0.039	0.353	0.217	0.134	0.081	0.073	0.003	0.213	0.041	0.062	0.048	0.389	0.231	0.240	0.214	0.247	0.351	0.171	0.342	0.267	0.446	0.293	0.204	0.132	0.294	0.559	1.000	0.479	0.152
Q7_14	0.229	0.217	0.230	0.313	0.172	0.431	0.337	0.166	0.213	0.338	0.312	0.193	0.083	0.278	0.207	0.160	0.160	0.295	0.266	0.270	0.327	0.246	0.379	0.363	0.376	0.215	0.344	0.278	0.284	0.309	0.349	0.071	0.145	0.163	0.075	0.169	0.078	0.141	0.110	0.275	0.284	0.399	0.273	0.378	0.497	0.382	0.437	0.527	0.588	0.419	0.296	0.213	0.387	0.492	0.479	1.000	0.297
Q7_15	0.502	0.522	0.463	0.539	0.543	0.523	0.332	0.446	0.384	0.506	0.566	0.428	0.398	0.487	0.501	0.483	0.455	0.584	0.515	0.487	0.444	0.486	0.344	0.300	0.452	0.369	0.422	0.565	0.397	0.473	0.494	0.464	0.388	0.415	0.311	0.408	0.536	0.515	0.516	0.400	0.485	0.525	0.702	0.570	0.370	0.558	0.562	0.413	0.333	0.435	0.654	0.761	0.524	0.397	0.152	0.297	1.000

# Difference between correlation matrices
kable(corr.pc$rho-corr.ppm,digits=3,format = "html")%>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%", height="500px")

	Q4_1	Q4_2	Q4_3	Q4_4	Q4_5	Q4_6	Q4_7	Q4_8	Q4_9	Q4_10	Q4_11	Q4_12	Q4_13	Q4_14	Q4_15	Q4_16	Q4_17	Q4_18	Q4_19	Q5_1	Q5_2	Q5_3	Q5_4	Q5_5	Q5_6	Q5_7	Q5_8	Q5_9	Q5_10	Q5_11	Q5_12	Q6_1	Q6_2	Q6_3	Q6_4	Q6_5	Q6_6	Q6_7	Q6_8	Q6_9	Q6_10	Q6_11	Q7_1	Q7_2	Q7_3	Q7_4	Q7_5	Q7_6	Q7_7	Q7_8	Q7_9	Q7_10	Q7_11	Q7_12	Q7_13	Q7_14	Q7_15
Q4_1	0.000	0.072	0.076	0.080	0.066	0.049	0.032	0.070	0.060	0.075	0.062	0.063	0.092	0.064	0.069	0.066	0.065	0.079	0.063	0.052	0.040	0.045	0.031	0.036	0.044	0.042	0.028	0.055	0.054	0.052	0.034	0.077	0.050	0.069	0.050	0.050	0.066	0.065	0.057	0.042	0.036	0.047	0.058	0.050	0.019	0.038	0.046	0.049	0.047	0.034	0.058	0.075	0.061	0.044	0.007	0.011	0.057
Q4_2	0.072	0.000	0.076	0.081	0.073	0.065	0.039	0.072	0.062	0.077	0.069	0.069	0.097	0.050	0.071	0.064	0.067	0.074	0.063	0.066	0.053	0.059	0.049	0.046	0.065	0.043	0.054	0.066	0.076	0.060	0.053	0.086	0.057	0.066	0.042	0.060	0.084	0.076	0.058	0.052	0.046	0.061	0.074	0.066	0.030	0.046	0.072	0.058	0.059	0.055	0.066	0.086	0.075	0.034	0.008	0.020	0.069
Q4_3	0.076	0.076	0.000	0.086	0.060	0.049	0.020	0.074	0.071	0.079	0.060	0.058	0.082	0.043	0.063	0.059	0.066	0.072	0.063	0.054	0.040	0.044	0.026	0.035	0.059	0.040	0.038	0.056	0.050	0.058	0.030	0.090	0.043	0.069	0.041	0.065	0.061	0.065	0.047	0.045	0.035	0.046	0.055	0.042	0.018	0.036	0.048	0.053	0.034	0.042	0.058	0.069	0.064	0.029	0.006	0.019	0.052
Q4_4	0.080	0.081	0.086	0.000	0.072	0.055	0.039	0.081	0.074	0.090	0.068	0.083	0.085	0.048	0.064	0.066	0.084	0.086	0.064	0.056	0.033	0.051	0.031	0.034	0.049	0.040	0.035	0.056	0.052	0.049	0.044	0.071	0.059	0.085	0.047	0.065	0.106	0.071	0.062	0.055	0.035	0.045	0.067	0.057	0.016	0.056	0.053	0.054	0.028	0.038	0.058	0.081	0.075	0.017	0.008	0.006	0.062
Q4_5	0.066	0.073	0.060	0.072	0.000	0.059	0.039	0.058	0.045	0.075	0.062	0.072	0.109	0.060	0.066	0.062	0.065	0.068	0.065	0.057	0.052	0.052	0.059	0.048	0.054	0.048	0.054	0.066	0.072	0.058	0.058	0.073	0.057	0.074	0.052	0.052	0.080	0.076	0.062	0.050	0.051	0.058	0.068	0.060	0.038	0.053	0.055	0.057	0.051	0.053	0.068	0.071	0.061	0.033	-0.007	-0.001	0.069
Q4_6	0.049	0.065	0.049	0.055	0.059	0.000	0.070	0.056	0.042	0.061	0.047	0.053	0.079	0.045	0.050	0.054	0.052	0.066	0.054	0.040	0.044	0.046	0.037	0.033	0.044	0.040	0.036	0.052	0.036	0.042	0.040	0.060	0.055	0.060	0.038	0.034	0.063	0.054	0.045	0.037	0.045	0.043	0.056	0.051	0.032	0.038	0.034	0.038	0.065	0.033	0.049	0.065	0.050	0.029	0.026	0.031	0.057
Q4_7	0.032	0.039	0.020	0.039	0.039	0.070	0.000	0.024	0.019	0.030	0.045	0.049	0.026	0.047	0.033	0.046	0.041	0.033	0.037	0.036	0.024	0.030	0.020	0.009	0.043	0.065	0.034	0.049	0.042	0.041	0.035	0.048	0.050	0.053	0.045	0.024	0.065	0.043	0.057	0.040	0.039	0.045	0.047	0.050	0.030	0.039	0.035	0.025	0.035	0.018	0.035	0.051	0.041	0.012	0.018	0.002	0.048
Q4_8	0.070	0.072	0.074	0.081	0.058	0.056	0.024	0.000	0.057	0.081	0.062	0.067	0.097	0.060	0.064	0.059	0.068	0.077	0.073	0.050	0.047	0.052	0.030	0.030	0.048	0.043	0.048	0.053	0.057	0.046	0.045	0.069	0.046	0.073	0.045	0.052	0.071	0.067	0.054	0.051	0.046	0.057	0.061	0.059	0.028	0.037	0.049	0.055	0.047	0.052	0.056	0.064	0.064	0.025	0.003	0.010	0.049
Q4_9	0.060	0.062	0.071	0.074	0.045	0.042	0.019	0.057	0.000	0.073	0.053	0.053	0.092	0.051	0.064	0.054	0.055	0.066	0.060	0.051	0.044	0.042	0.031	0.042	0.048	0.046	0.038	0.051	0.053	0.051	0.051	0.078	0.037	0.079	0.039	0.056	0.062	0.063	0.052	0.044	0.028	0.042	0.060	0.069	0.031	0.044	0.057	0.056	0.046	0.048	0.058	0.061	0.071	0.040	0.006	0.015	0.044
Q4_10	0.075	0.077	0.079	0.090	0.075	0.061	0.030	0.081	0.073	0.000	0.072	0.096	0.114	0.055	0.081	0.076	0.081	0.103	0.087	0.066	0.025	0.062	0.044	0.043	0.055	0.053	0.051	0.069	0.066	0.060	0.053	0.083	0.071	0.103	0.067	0.074	0.103	0.106	0.082	0.067	0.047	0.060	0.066	0.075	0.042	0.048	0.059	0.058	0.046	0.050	0.057	0.089	0.075	0.024	0.018	0.021	0.066
Q4_11	0.062	0.069	0.060	0.068	0.062	0.047	0.045	0.062	0.053	0.072	0.000	0.077	0.114	0.055	0.061	0.060	0.065	0.074	0.060	0.052	0.041	0.048	0.037	0.036	0.045	0.051	0.043	0.057	0.064	0.054	0.041	0.077	0.053	0.072	0.047	0.058	0.072	0.071	0.068	0.054	0.039	0.054	0.063	0.064	0.033	0.043	0.057	0.059	0.051	0.045	0.049	0.058	0.074	0.046	0.022	0.020	0.058
Q4_12	0.063	0.069	0.058	0.083	0.072	0.053	0.049	0.067	0.053	0.096	0.077	0.000	0.121	0.085	0.064	0.071	0.063	0.081	0.062	0.059	0.054	0.051	0.053	0.041	0.056	0.069	0.054	0.068	0.083	0.051	0.054	0.092	0.068	0.094	0.058	0.079	0.099	0.083	0.086	0.066	0.057	0.074	0.070	0.084	0.063	0.051	0.070	0.057	0.064	0.053	0.060	0.057	0.067	0.046	0.007	0.013	0.058
Q4_13	0.092	0.097	0.082	0.085	0.109	0.079	0.026	0.097	0.092	0.114	0.114	0.121	0.000	0.133	0.086	0.092	0.067	0.118	0.118	0.115	0.109	0.099	0.042	0.032	0.082	0.092	0.083	0.099	0.110	0.085	0.093	0.121	0.098	0.102	0.092	0.116	0.099	0.130	0.096	0.116	0.059	0.095	0.116	0.114	0.056	0.064	0.104	0.114	0.056	0.076	0.100	0.103	0.094	0.079	-0.012	-0.013	0.083
Q4_14	0.064	0.050	0.043	0.048	0.060	0.045	0.047	0.060	0.051	0.055	0.055	0.085	0.133	0.000	0.071	0.069	0.058	0.067	0.059	0.055	0.040	0.058	0.034	0.025	0.049	0.046	0.043	0.058	0.049	0.059	0.032	0.102	0.071	0.086	0.063	0.066	0.079	0.086	0.081	0.066	0.058	0.047	0.058	0.047	0.028	0.033	0.046	0.057	0.053	0.033	0.055	0.070	0.053	0.051	0.022	0.006	0.060
Q4_15	0.069	0.071	0.063	0.064	0.066	0.050	0.033	0.064	0.064	0.081	0.061	0.064	0.086	0.071	0.000	0.073	0.064	0.079	0.066	0.053	0.046	0.059	0.053	0.037	0.065	0.056	0.052	0.063	0.065	0.051	0.050	0.066	0.060	0.079	0.051	0.054	0.078	0.077	0.063	0.051	0.045	0.053	0.063	0.066	0.029	0.041	0.059	0.068	0.052	0.055	0.056	0.061	0.071	0.044	0.008	0.007	0.054
Q4_16	0.066	0.064	0.059	0.066	0.062	0.054	0.046	0.059	0.054	0.076	0.060	0.071	0.092	0.069	0.073	0.000	0.072	0.073	0.063	0.049	0.040	0.059	0.038	0.031	0.066	0.053	0.045	0.062	0.060	0.053	0.047	0.095	0.071	0.084	0.061	0.043	0.085	0.072	0.066	0.050	0.048	0.049	0.057	0.054	0.017	0.037	0.048	0.052	0.028	0.035	0.054	0.066	0.053	0.036	0.004	-0.004	0.060
Q4_17	0.065	0.067	0.066	0.084	0.065	0.052	0.041	0.068	0.055	0.081	0.065	0.063	0.067	0.058	0.064	0.072	0.000	0.076	0.066	0.057	0.053	0.048	0.034	0.026	0.054	0.054	0.045	0.055	0.070	0.051	0.046	0.073	0.041	0.075	0.050	0.039	0.077	0.070	0.056	0.048	0.057	0.048	0.055	0.056	0.037	0.047	0.058	0.054	0.049	0.055	0.060	0.060	0.067	0.029	-0.007	0.011	0.056
Q4_18	0.079	0.074	0.072	0.086	0.068	0.066	0.033	0.077	0.066	0.103	0.074	0.081	0.118	0.067	0.079	0.073	0.076	0.000	0.072	0.067	0.058	0.060	0.046	0.051	0.069	0.058	0.061	0.075	0.088	0.054	0.054	0.084	0.052	0.084	0.049	0.051	0.084	0.082	0.061	0.058	0.053	0.064	0.073	0.071	0.031	0.054	0.060	0.057	0.054	0.050	0.062	0.076	0.092	0.040	0.000	0.024	0.072
Q4_19	0.063	0.063	0.063	0.064	0.065	0.054	0.037	0.073	0.060	0.087	0.060	0.062	0.118	0.059	0.066	0.063	0.066	0.072	0.000	0.058	0.049	0.051	0.032	0.031	0.053	0.057	0.044	0.065	0.061	0.051	0.049	0.095	0.055	0.091	0.060	0.060	0.083	0.079	0.064	0.062	0.049	0.053	0.066	0.054	0.046	0.044	0.050	0.054	0.061	0.063	0.061	0.061	0.074	0.050	0.004	0.018	0.057
Q5_1	0.052	0.066	0.054	0.056	0.057	0.040	0.036	0.050	0.051	0.066	0.052	0.059	0.115	0.055	0.053	0.049	0.057	0.067	0.058	0.000	0.044	0.057	0.047	0.036	0.056	0.044	0.051	0.057	0.066	0.054	0.052	0.078	0.038	0.049	0.027	0.062	0.075	0.052	0.048	0.056	0.028	0.048	0.057	0.049	0.024	0.033	0.047	0.042	0.043	0.034	0.051	0.051	0.069	0.041	0.011	0.014	0.052
Q5_2	0.040	0.053	0.040	0.033	0.052	0.044	0.024	0.047	0.044	0.025	0.041	0.054	0.109	0.040	0.046	0.040	0.053	0.058	0.049	0.044	0.000	0.057	0.021	0.016	0.049	0.034	0.030	0.046	0.036	0.037	0.031	0.073	0.044	0.067	0.046	0.053	0.070	0.054	0.054	0.042	0.026	0.039	0.039	0.027	0.001	0.022	0.029	0.029	0.042	0.014	0.039	0.057	0.024	0.004	0.010	0.000	0.041
Q5_3	0.045	0.059	0.044	0.051	0.052	0.046	0.030	0.052	0.042	0.062	0.048	0.051	0.099	0.058	0.059	0.059	0.048	0.060	0.051	0.057	0.057	0.000	0.052	0.043	0.061	0.044	0.053	0.056	0.057	0.051	0.047	0.086	0.049	0.058	0.041	0.043	0.065	0.053	0.055	0.051	0.038	0.046	0.056	0.055	0.020	0.033	0.042	0.046	0.044	0.040	0.050	0.054	0.048	0.023	0.007	0.004	0.051
Q5_4	0.031	0.049	0.026	0.031	0.059	0.037	0.020	0.030	0.031	0.044	0.037	0.053	0.042	0.034	0.053	0.038	0.034	0.046	0.032	0.047	0.021	0.052	0.000	0.056	0.046	0.019	0.047	0.055	0.037	0.062	0.046	0.021	0.021	0.037	0.007	0.032	0.034	0.017	0.019	0.049	0.022	0.028	0.037	0.023	0.040	0.017	0.026	0.034	0.063	0.051	0.026	0.045	0.017	0.032	0.023	0.009	0.034
Q5_5	0.036	0.046	0.035	0.034	0.048	0.033	0.009	0.030	0.042	0.043	0.036	0.041	0.032	0.025	0.037	0.031	0.026	0.051	0.031	0.036	0.016	0.043	0.056	0.000	0.041	0.014	0.043	0.051	0.037	0.060	0.045	0.025	0.032	0.036	0.015	0.040	0.020	0.021	0.021	0.043	0.012	0.017	0.039	0.022	0.030	0.011	0.015	0.031	0.039	0.034	0.029	0.050	0.008	0.022	0.024	0.015	0.034
Q5_6	0.044	0.065	0.059	0.049	0.054	0.044	0.043	0.048	0.048	0.055	0.045	0.056	0.082	0.049	0.065	0.066	0.054	0.069	0.053	0.056	0.049	0.061	0.046	0.041	0.000	0.031	0.049	0.060	0.029	0.061	0.048	0.057	0.048	0.063	0.037	0.057	0.053	0.056	0.057	0.039	0.045	0.034	0.050	0.019	0.022	0.028	0.039	0.043	0.048	0.032	0.051	0.066	0.055	0.026	0.011	0.004	0.048
Q5_7	0.042	0.043	0.040	0.040	0.048	0.040	0.065	0.043	0.046	0.053	0.051	0.069	0.092	0.046	0.056	0.053	0.054	0.058	0.057	0.044	0.034	0.044	0.019	0.014	0.031	0.000	0.035	0.056	0.051	0.049	0.030	0.083	0.062	0.084	0.051	0.057	0.072	0.080	0.073	0.062	0.043	0.050	0.055	0.049	0.043	0.034	0.037	0.038	0.030	0.028	0.050	0.048	0.049	0.027	0.016	0.004	0.038
Q5_8	0.028	0.054	0.038	0.035	0.054	0.036	0.034	0.048	0.038	0.051	0.043	0.054	0.083	0.043	0.052	0.045	0.045	0.061	0.044	0.051	0.030	0.053	0.047	0.043	0.049	0.035	0.000	0.056	0.050	0.051	0.036	0.058	0.043	0.062	0.032	0.063	0.057	0.041	0.048	0.040	0.039	0.038	0.047	0.037	0.024	0.034	0.028	0.044	0.039	0.041	0.040	0.050	0.039	0.025	0.017	0.021	0.042
Q5_9	0.055	0.066	0.056	0.056	0.066	0.052	0.049	0.053	0.051	0.069	0.057	0.068	0.099	0.058	0.063	0.062	0.055	0.075	0.065	0.057	0.046	0.056	0.055	0.051	0.060	0.056	0.056	0.000	0.074	0.054	0.049	0.088	0.062	0.069	0.050	0.059	0.071	0.067	0.063	0.058	0.053	0.056	0.058	0.051	0.032	0.043	0.047	0.045	0.036	0.042	0.056	0.056	0.064	0.034	0.000	0.014	0.059
Q5_10	0.054	0.076	0.050	0.052	0.072	0.036	0.042	0.057	0.053	0.066	0.064	0.083	0.110	0.049	0.065	0.060	0.070	0.088	0.061	0.066	0.036	0.057	0.037	0.037	0.029	0.051	0.050	0.074	0.000	0.072	0.035	0.081	0.057	0.090	0.050	0.061	0.105	0.078	0.070	0.067	0.034	0.034	0.064	0.050	0.005	0.042	0.051	0.050	0.051	0.042	0.055	0.081	0.063	0.024	-0.001	0.004	0.054
Q5_11	0.052	0.060	0.058	0.049	0.058	0.042	0.041	0.046	0.051	0.060	0.054	0.051	0.085	0.059	0.051	0.053	0.051	0.054	0.051	0.054	0.037	0.051	0.062	0.060	0.061	0.049	0.051	0.054	0.072	0.000	0.054	0.083	0.052	0.049	0.029	0.055	0.064	0.055	0.052	0.042	0.056	0.047	0.061	0.046	0.049	0.046	0.046	0.049	0.069	0.048	0.055	0.056	0.057	0.056	0.036	0.030	0.050
Q5_12	0.034	0.053	0.030	0.044	0.058	0.040	0.035	0.045	0.051	0.053	0.041	0.054	0.093	0.032	0.050	0.047	0.046	0.054	0.049	0.052	0.031	0.047	0.046	0.045	0.048	0.030	0.036	0.049	0.035	0.054	0.000	0.067	0.060	0.063	0.040	0.046	0.075	0.055	0.056	0.049	0.028	0.039	0.055	0.031	0.018	0.036	0.033	0.027	0.031	0.032	0.056	0.065	0.043	0.017	0.017	-0.005	0.048
Q6_1	0.077	0.086	0.090	0.071	0.073	0.060	0.048	0.069	0.078	0.083	0.077	0.092	0.121	0.102	0.066	0.095	0.073	0.084	0.095	0.078	0.073	0.086	0.021	0.025	0.057	0.083	0.058	0.088	0.081	0.083	0.067	0.000	0.093	0.102	0.090	0.095	0.098	0.113	0.100	0.072	0.066	0.075	0.100	0.084	0.025	0.057	0.066	0.077	0.024	0.046	0.100	0.081	0.071	0.063	0.010	-0.009	0.100
Q6_2	0.050	0.057	0.043	0.059	0.057	0.055	0.050	0.046	0.037	0.071	0.053	0.068	0.098	0.071	0.060	0.071	0.041	0.052	0.055	0.038	0.044	0.049	0.021	0.032	0.048	0.062	0.043	0.062	0.057	0.052	0.060	0.093	0.000	0.078	0.064	0.082	0.077	0.076	0.076	0.046	0.042	0.058	0.062	0.061	0.024	0.038	0.048	0.046	0.007	0.034	0.054	0.051	0.046	0.013	-0.013	-0.005	0.044
Q6_3	0.069	0.066	0.069	0.085	0.074	0.060	0.053	0.073	0.079	0.103	0.072	0.094	0.102	0.086	0.079	0.084	0.075	0.084	0.091	0.049	0.067	0.058	0.037	0.036	0.063	0.084	0.062	0.069	0.090	0.049	0.063	0.102	0.078	0.000	0.091	0.087	0.098	0.099	0.090	0.069	0.047	0.077	0.088	0.079	0.048	0.054	0.067	0.075	0.033	0.041	0.076	0.077	0.070	0.013	-0.022	-0.001	0.069
Q6_4	0.050	0.042	0.041	0.047	0.052	0.038	0.045	0.045	0.039	0.067	0.047	0.058	0.092	0.063	0.051	0.061	0.050	0.049	0.060	0.027	0.046	0.041	0.007	0.015	0.037	0.051	0.032	0.050	0.050	0.029	0.040	0.090	0.064	0.091	0.000	0.060	0.078	0.073	0.079	0.035	0.039	0.055	0.047	0.046	0.019	0.040	0.036	0.039	-0.002	0.022	0.045	0.054	0.045	0.003	-0.019	-0.021	0.033
Q6_5	0.050	0.060	0.065	0.065	0.052	0.034	0.024	0.052	0.056	0.074	0.058	0.079	0.116	0.066	0.054	0.043	0.039	0.051	0.060	0.062	0.053	0.043	0.032	0.040	0.057	0.057	0.063	0.059	0.061	0.055	0.046	0.095	0.082	0.087	0.060	0.000	0.081	0.063	0.070	0.057	0.055	0.055	0.078	0.074	0.027	0.049	0.046	0.055	0.028	0.038	0.064	0.063	0.059	0.035	0.002	0.016	0.063
Q6_6	0.066	0.084	0.061	0.106	0.080	0.063	0.065	0.071	0.062	0.103	0.072	0.099	0.099	0.079	0.078	0.085	0.077	0.084	0.083	0.075	0.070	0.065	0.034	0.020	0.053	0.072	0.057	0.071	0.105	0.064	0.075	0.098	0.077	0.098	0.078	0.081	0.000	0.105	0.088	0.083	0.056	0.108	0.090	0.086	0.030	0.075	0.080	0.077	0.017	0.065	0.077	0.079	0.089	0.025	-0.019	-0.027	0.091
Q6_7	0.065	0.076	0.065	0.071	0.076	0.054	0.043	0.067	0.063	0.106	0.071	0.083	0.130	0.086	0.077	0.072	0.070	0.082	0.079	0.052	0.054	0.053	0.017	0.021	0.056	0.080	0.041	0.067	0.078	0.055	0.055	0.113	0.076	0.099	0.073	0.063	0.105	0.000	0.086	0.067	0.057	0.082	0.075	0.070	0.046	0.055	0.065	0.052	0.037	0.047	0.059	0.069	0.070	0.027	-0.013	-0.011	0.071
Q6_8	0.057	0.058	0.047	0.062	0.062	0.045	0.057	0.054	0.052	0.082	0.068	0.086	0.096	0.081	0.063	0.066	0.056	0.061	0.064	0.048	0.054	0.055	0.019	0.021	0.057	0.073	0.048	0.063	0.070	0.052	0.056	0.100	0.076	0.090	0.079	0.070	0.088	0.086	0.000	0.066	0.049	0.069	0.067	0.068	0.043	0.064	0.063	0.060	0.018	0.040	0.062	0.052	0.072	0.024	-0.008	0.002	0.059
Q6_9	0.042	0.052	0.045	0.055	0.050	0.037	0.040	0.051	0.044	0.067	0.054	0.066	0.116	0.066	0.051	0.050	0.048	0.058	0.062	0.056	0.042	0.051	0.049	0.043	0.039	0.062	0.040	0.058	0.067	0.042	0.049	0.072	0.046	0.069	0.035	0.057	0.083	0.067	0.066	0.000	0.067	0.065	0.067	0.066	0.055	0.050	0.064	0.056	0.068	0.052	0.059	0.059	0.066	0.071	0.038	0.036	0.063
Q6_10	0.036	0.046	0.035	0.035	0.051	0.045	0.039	0.046	0.028	0.047	0.039	0.057	0.059	0.058	0.045	0.048	0.057	0.053	0.049	0.028	0.026	0.038	0.022	0.012	0.045	0.043	0.039	0.053	0.034	0.056	0.028	0.066	0.042	0.047	0.039	0.055	0.056	0.057	0.049	0.067	0.000	0.053	0.051	0.015	0.023	0.025	0.034	0.030	0.069	0.037	0.049	0.062	0.045	0.049	0.033	0.021	0.057
Q6_11	0.047	0.061	0.046	0.045	0.058	0.043	0.045	0.057	0.042	0.060	0.054	0.074	0.095	0.047	0.053	0.049	0.048	0.064	0.053	0.048	0.039	0.046	0.028	0.017	0.034	0.050	0.038	0.056	0.034	0.047	0.039	0.075	0.058	0.077	0.055	0.055	0.108	0.082	0.069	0.065	0.053	0.000	0.059	0.038	0.024	0.030	0.047	0.039	0.039	0.028	0.048	0.062	0.048	0.026	0.023	0.021	0.058
Q7_1	0.058	0.074	0.055	0.067	0.068	0.056	0.047	0.061	0.060	0.066	0.063	0.070	0.116	0.058	0.063	0.057	0.055	0.073	0.066	0.057	0.039	0.056	0.037	0.039	0.050	0.055	0.047	0.058	0.064	0.061	0.055	0.100	0.062	0.088	0.047	0.078	0.090	0.075	0.067	0.067	0.051	0.059	0.000	0.069	0.042	0.052	0.054	0.054	0.038	0.048	0.057	0.081	0.069	0.041	0.019	0.003	0.070
Q7_2	0.050	0.066	0.042	0.057	0.060	0.051	0.050	0.059	0.069	0.075	0.064	0.084	0.114	0.047	0.066	0.054	0.056	0.071	0.054	0.049	0.027	0.055	0.023	0.022	0.019	0.049	0.037	0.051	0.050	0.046	0.031	0.084	0.061	0.079	0.046	0.074	0.086	0.070	0.068	0.066	0.015	0.038	0.069	0.000	0.058	0.045	0.033	0.029	0.044	0.030	0.047	0.075	0.045	0.030	0.029	0.010	0.068
Q7_3	0.019	0.030	0.018	0.016	0.038	0.032	0.030	0.028	0.031	0.042	0.033	0.063	0.056	0.028	0.029	0.017	0.037	0.031	0.046	0.024	0.001	0.020	0.040	0.030	0.022	0.043	0.024	0.032	0.005	0.049	0.018	0.025	0.024	0.048	0.019	0.027	0.030	0.046	0.043	0.055	0.023	0.024	0.042	0.058	0.000	0.044	0.025	0.049	0.071	0.033	0.017	0.039	0.020	0.041	0.027	0.012	0.036
Q7_4	0.038	0.046	0.036	0.056	0.053	0.038	0.039	0.037	0.044	0.048	0.043	0.051	0.064	0.033	0.041	0.037	0.047	0.054	0.044	0.033	0.022	0.033	0.017	0.011	0.028	0.034	0.034	0.043	0.042	0.046	0.036	0.057	0.038	0.054	0.040	0.049	0.075	0.055	0.064	0.050	0.025	0.030	0.052	0.045	0.044	0.000	0.037	0.036	0.037	0.044	0.046	0.063	0.052	0.029	0.016	0.022	0.053
Q7_5	0.046	0.072	0.048	0.053	0.055	0.034	0.035	0.049	0.057	0.059	0.057	0.070	0.104	0.046	0.059	0.048	0.058	0.060	0.050	0.047	0.029	0.042	0.026	0.015	0.039	0.037	0.028	0.047	0.051	0.046	0.033	0.066	0.048	0.067	0.036	0.046	0.080	0.065	0.063	0.064	0.034	0.047	0.054	0.033	0.025	0.037	0.000	0.044	0.067	0.053	0.048	0.065	0.050	0.037	0.043	0.025	0.056
Q7_6	0.049	0.058	0.053	0.054	0.057	0.038	0.025	0.055	0.056	0.058	0.059	0.057	0.114	0.057	0.068	0.052	0.054	0.057	0.054	0.042	0.029	0.046	0.034	0.031	0.043	0.038	0.044	0.045	0.050	0.049	0.027	0.077	0.046	0.075	0.039	0.055	0.077	0.052	0.060	0.056	0.030	0.039	0.054	0.029	0.049	0.036	0.044	0.000	0.058	0.042	0.043	0.071	0.050	0.045	0.033	0.040	0.045
Q7_7	0.047	0.059	0.034	0.028	0.051	0.065	0.035	0.047	0.046	0.046	0.051	0.064	0.056	0.053	0.052	0.028	0.049	0.054	0.061	0.043	0.042	0.044	0.063	0.039	0.048	0.030	0.039	0.036	0.051	0.069	0.031	0.024	0.007	0.033	-0.002	0.028	0.017	0.037	0.018	0.068	0.069	0.039	0.038	0.044	0.071	0.037	0.067	0.058	0.000	0.042	0.043	0.049	0.034	0.072	0.068	0.057	0.046
Q7_8	0.034	0.055	0.042	0.038	0.053	0.033	0.018	0.052	0.048	0.050	0.045	0.053	0.076	0.033	0.055	0.035	0.055	0.050	0.063	0.034	0.014	0.040	0.051	0.034	0.032	0.028	0.041	0.042	0.042	0.048	0.032	0.046	0.034	0.041	0.022	0.038	0.065	0.047	0.040	0.052	0.037	0.028	0.048	0.030	0.033	0.044	0.053	0.042	0.042	0.000	0.057	0.067	0.059	0.048	0.038	0.026	0.046
Q7_9	0.058	0.066	0.058	0.058	0.068	0.049	0.035	0.056	0.058	0.057	0.049	0.060	0.100	0.055	0.056	0.054	0.060	0.062	0.061	0.051	0.039	0.050	0.026	0.029	0.051	0.050	0.040	0.056	0.055	0.055	0.056	0.100	0.054	0.076	0.045	0.064	0.077	0.059	0.062	0.059	0.049	0.048	0.057	0.047	0.017	0.046	0.048	0.043	0.043	0.057	0.000	0.069	0.065	0.031	0.017	0.019	0.061
Q7_10	0.075	0.086	0.069	0.081	0.071	0.065	0.051	0.064	0.061	0.089	0.058	0.057	0.103	0.070	0.061	0.066	0.060	0.076	0.061	0.051	0.057	0.054	0.045	0.050	0.066	0.048	0.050	0.056	0.081	0.056	0.065	0.081	0.051	0.077	0.054	0.063	0.079	0.069	0.052	0.059	0.062	0.062	0.081	0.075	0.039	0.063	0.065	0.071	0.049	0.067	0.069	0.000	0.086	0.035	0.006	0.023	0.081
Q7_11	0.061	0.075	0.064	0.075	0.061	0.050	0.041	0.064	0.071	0.075	0.074	0.067	0.094	0.053	0.071	0.053	0.067	0.092	0.074	0.069	0.024	0.048	0.017	0.008	0.055	0.049	0.039	0.064	0.063	0.057	0.043	0.071	0.046	0.070	0.045	0.059	0.089	0.070	0.072	0.066	0.045	0.048	0.069	0.045	0.020	0.052	0.050	0.050	0.034	0.059	0.065	0.086	0.000	0.051	0.034	0.042	0.079
Q7_12	0.044	0.034	0.029	0.017	0.033	0.029	0.012	0.025	0.040	0.024	0.046	0.046	0.079	0.051	0.044	0.036	0.029	0.040	0.050	0.041	0.004	0.023	0.032	0.022	0.026	0.027	0.025	0.034	0.024	0.056	0.017	0.063	0.013	0.013	0.003	0.035	0.025	0.027	0.024	0.071	0.049	0.026	0.041	0.030	0.041	0.029	0.037	0.045	0.072	0.048	0.031	0.035	0.051	0.000	0.076	0.044	0.031
Q7_13	0.007	0.008	0.006	0.008	-0.007	0.026	0.018	0.003	0.006	0.018	0.022	0.007	-0.012	0.022	0.008	0.004	-0.007	0.000	0.004	0.011	0.010	0.007	0.023	0.024	0.011	0.016	0.017	0.000	-0.001	0.036	0.017	0.010	-0.013	-0.022	-0.019	0.002	-0.019	-0.013	-0.008	0.038	0.033	0.023	0.019	0.029	0.027	0.016	0.043	0.033	0.068	0.038	0.017	0.006	0.034	0.076	0.000	0.055	0.014
Q7_14	0.011	0.020	0.019	0.006	-0.001	0.031	0.002	0.010	0.015	0.021	0.020	0.013	-0.013	0.006	0.007	-0.004	0.011	0.024	0.018	0.014	0.000	0.004	0.009	0.015	0.004	0.004	0.021	0.014	0.004	0.030	-0.005	-0.009	-0.005	-0.001	-0.021	0.016	-0.027	-0.011	0.002	0.036	0.021	0.021	0.003	0.010	0.012	0.022	0.025	0.040	0.057	0.026	0.019	0.023	0.042	0.044	0.055	0.000	0.012
Q7_15	0.057	0.069	0.052	0.062	0.069	0.057	0.048	0.049	0.044	0.066	0.058	0.058	0.083	0.060	0.054	0.060	0.056	0.072	0.057	0.052	0.041	0.051	0.034	0.034	0.048	0.038	0.042	0.059	0.054	0.050	0.048	0.100	0.044	0.069	0.033	0.063	0.091	0.071	0.059	0.063	0.057	0.058	0.070	0.068	0.036	0.053	0.056	0.045	0.046	0.046	0.061	0.081	0.079	0.031	0.014	0.012	0.000

# What % of PC correlations are higher than PPM?
a <- sum(round(corr.pc$rho - corr.ppm, 3) > 0)/2
b <- sum(round(corr.pc$rho - corr.ppm, 3) < 0)/2
prop.diff <- a/(a+b)
prop.diff

[1] 0.9868173

# Is this difference significantly different than .5?
X <- table(c(rep(0,a),rep(1,b)))
prop.test(x=X, alternative = 'greater')

    1-sample proportions test with continuity correction

data:  X, null probability 0.5
X-squared = 1508.2, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is greater than 0.5
95 percent confidence interval:
 0.9808562 1.0000000
sample estimates:
        p 
0.9868173 

Eigenvalues and Scree Plot

evalues<-eigen(corr.pc$rho)$values
evalues

 [1] 2.627313e+01 3.761010e+00 2.952063e+00 2.210781e+00 1.460550e+00
 [6] 1.397493e+00 1.274058e+00 1.101728e+00 1.011097e+00 9.481728e-01
[11] 8.631385e-01 7.519192e-01 7.257157e-01 7.148329e-01 6.489492e-01
[16] 6.317037e-01 6.070564e-01 5.773193e-01 5.627900e-01 5.426212e-01
[21] 5.001011e-01 4.759799e-01 4.542633e-01 4.423228e-01 4.201005e-01
[26] 4.067098e-01 3.823340e-01 3.695824e-01 3.251477e-01 3.064071e-01
[31] 2.924240e-01 2.856197e-01 2.675262e-01 2.658989e-01 2.568959e-01
[36] 2.417409e-01 2.170894e-01 2.100147e-01 1.954760e-01 1.827397e-01
[41] 1.693641e-01 1.613067e-01 1.502327e-01 1.461206e-01 1.426707e-01
[46] 1.223941e-01 1.080088e-01 9.494902e-02 8.224543e-02 7.330500e-02
[51] 6.150090e-02 5.520100e-02 4.169916e-02 3.892286e-02 2.619869e-02
[56] 1.138168e-02 9.990371e-11

plotnScree(nScree(evalues, model="factors"), main="Scree Plot & Parallel Analysis")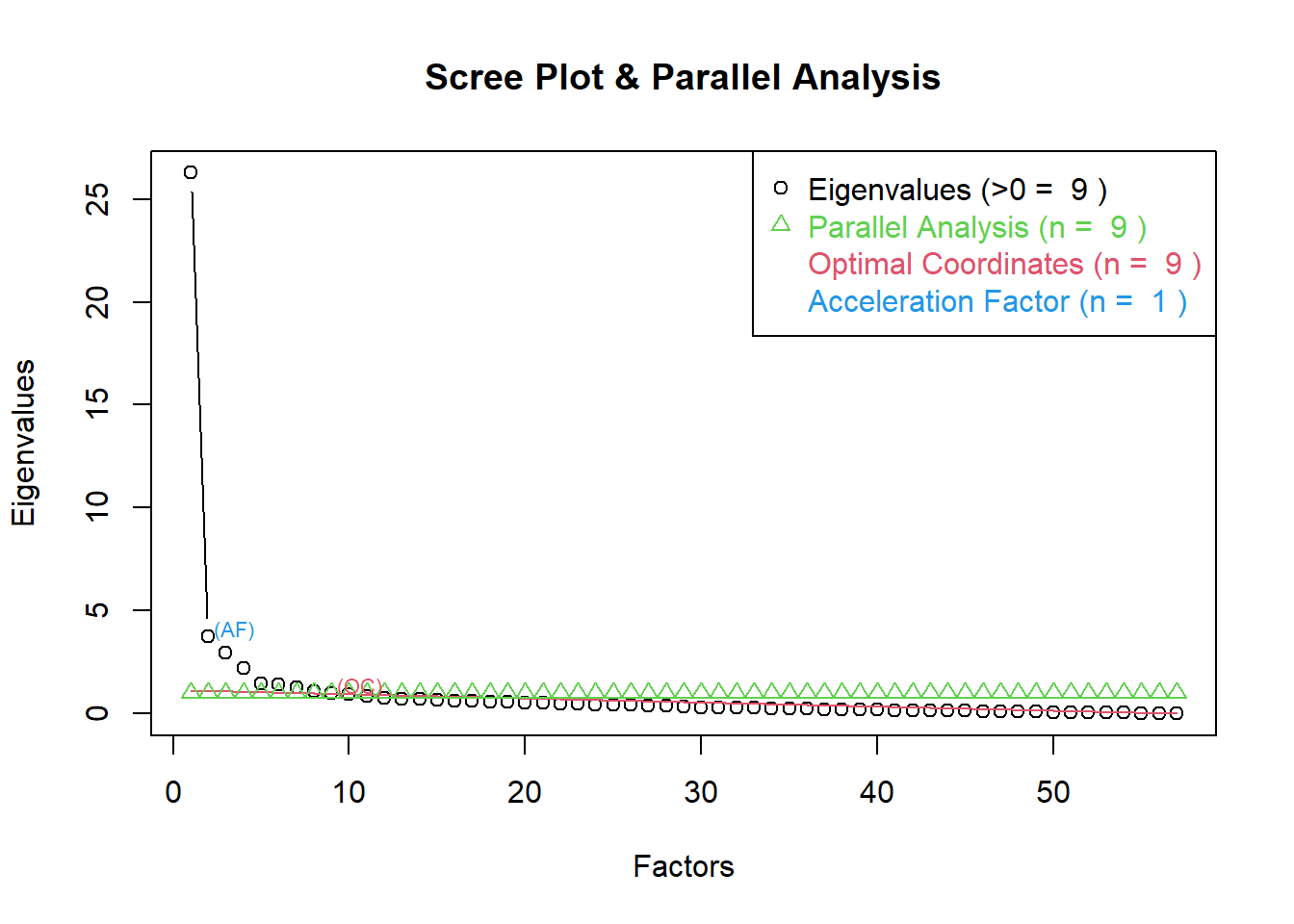

psych::fa.parallel(dat,main="Parallel Analysis",
                   fm = "pa",cor = "cov")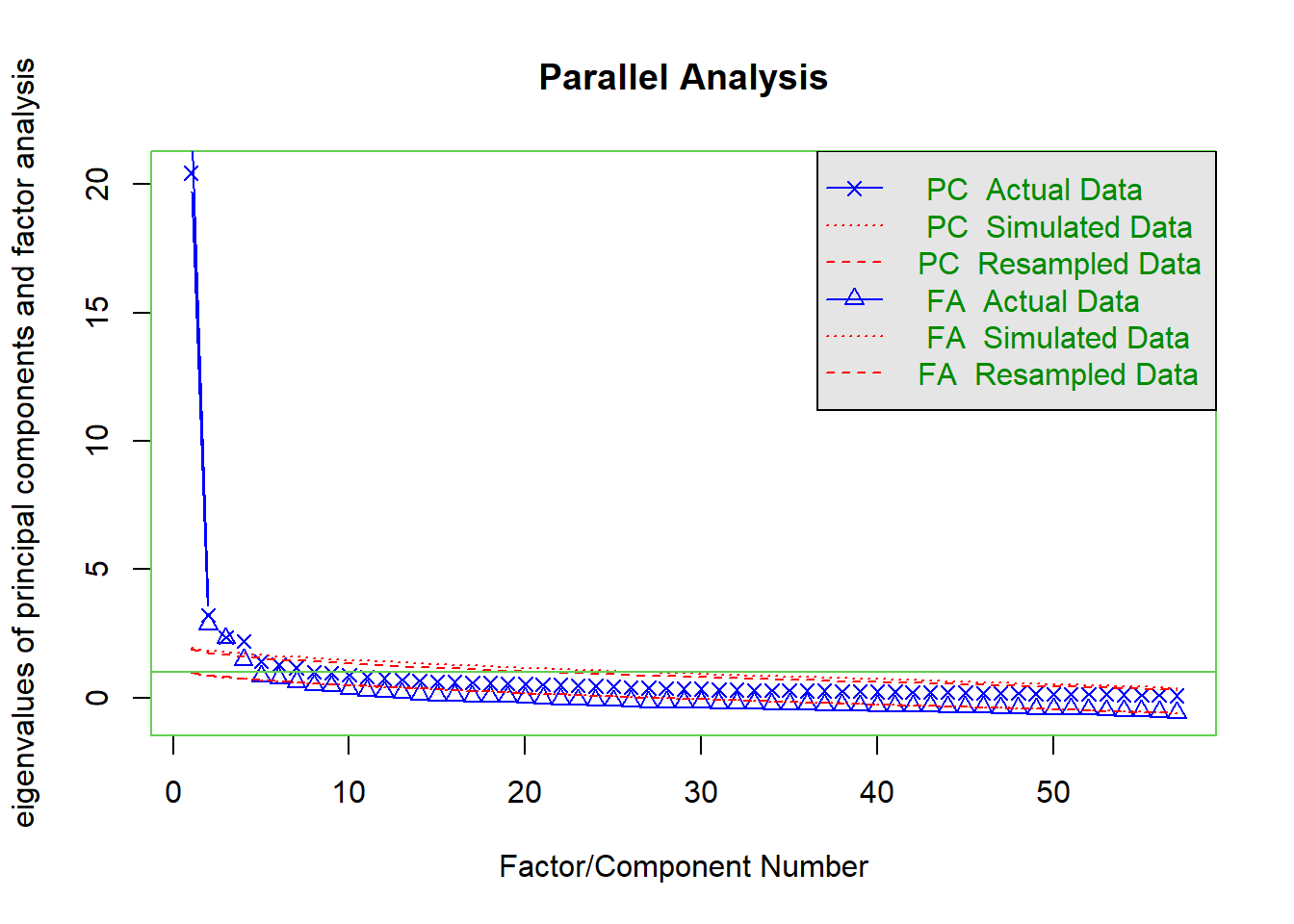

Parallel analysis suggests that the number of factors =  6  and the number of components =  4 

psych::fa.parallel(corr.pc$rho,main="Parallel Analysis",
                   n.obs = nrow(mydata), fm = "pa", cor = "cov")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.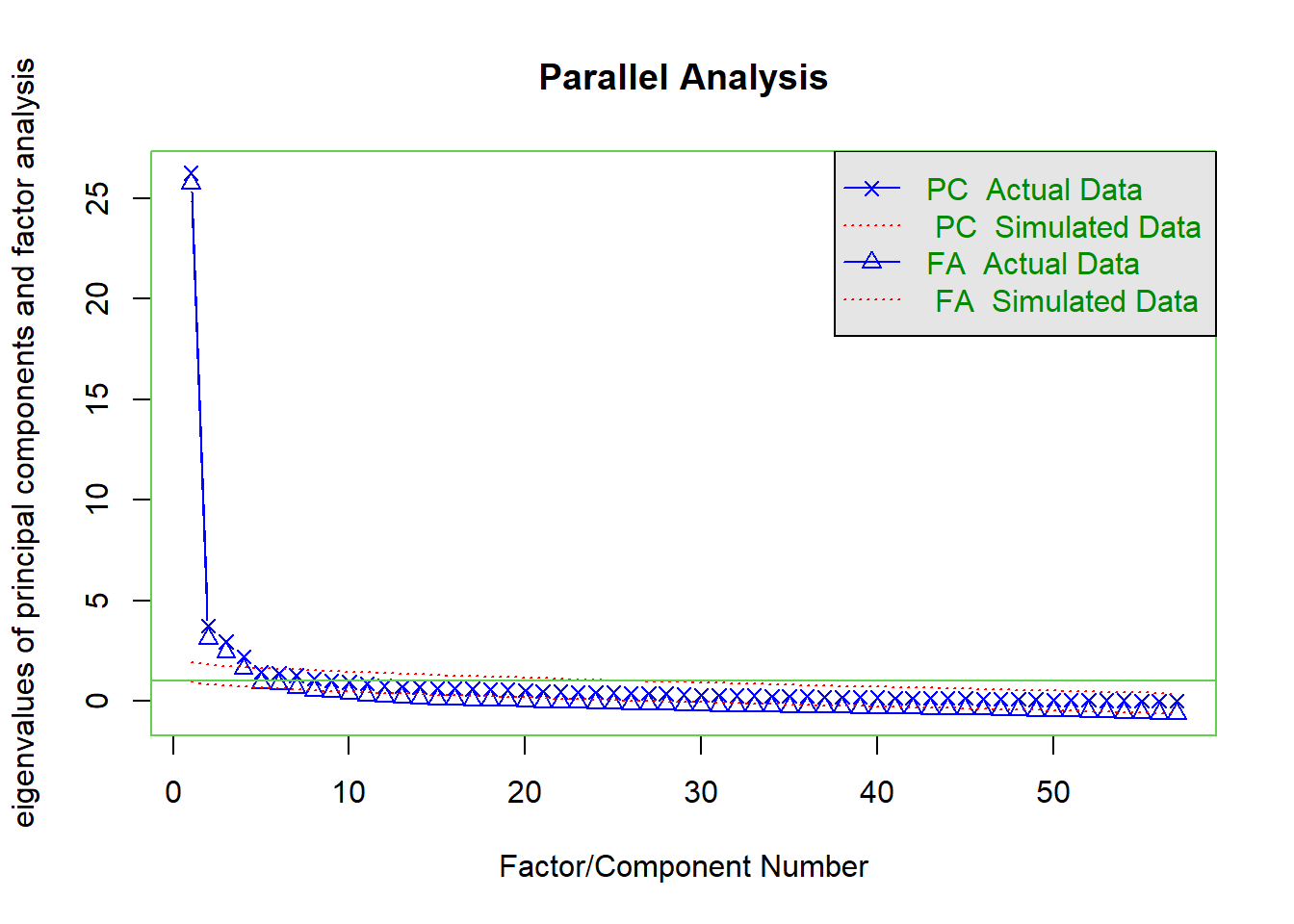

Parallel analysis suggests that the number of factors =  7  and the number of components =  4 

Note that the warning for the “estimated weights for the factor scores…” is not particularly impacting because we do not intend to obtain factor scores.

Factor Extraction

Two factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 2, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 2, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA1   PA2   h2   u2 com
Q4_1   0.41  0.33 0.47 0.53 1.9
Q4_2   0.43  0.36 0.55 0.45 1.9
Q4_3   0.36  0.39 0.48 0.52 2.0
Q4_4   0.33  0.48 0.57 0.43 1.8
Q4_5   0.52  0.27 0.54 0.46 1.5
Q4_6   0.25  0.48 0.47 0.53 1.5
Q4_7   0.05  0.55 0.34 0.66 1.0
Q4_8   0.58  0.18 0.52 0.48 1.2
Q4_9   0.38  0.32 0.43 0.57 1.9
Q4_10  0.36  0.42 0.53 0.47 2.0
Q4_11  0.46  0.37 0.60 0.40 1.9
Q4_12  0.70  0.07 0.56 0.44 1.0
Q4_13  0.80 -0.06 0.58 0.42 1.0
Q4_14  0.51  0.28 0.55 0.45 1.6
Q4_15  0.54  0.29 0.60 0.40 1.5
Q4_16  0.57  0.19 0.52 0.48 1.2
Q4_17  0.54  0.19 0.48 0.52 1.2
Q4_18  0.51  0.35 0.65 0.35 1.8
Q4_19  0.45  0.39 0.61 0.39 2.0
Q5_1   0.23  0.50 0.47 0.53 1.4
Q5_2   0.21  0.48 0.43 0.57 1.4
Q5_3   0.30  0.42 0.45 0.55 1.8
Q5_4  -0.16  0.77 0.43 0.57 1.1
Q5_5  -0.22  0.75 0.37 0.63 1.2
Q5_6   0.12  0.64 0.53 0.47 1.1
Q5_7   0.43  0.28 0.43 0.57 1.7
Q5_8   0.12  0.61 0.49 0.51 1.1
Q5_9   0.44  0.38 0.58 0.42 2.0
Q5_10  0.34  0.36 0.42 0.58 2.0
Q5_11  0.25  0.51 0.50 0.50 1.4
Q5_12  0.20  0.53 0.47 0.53 1.3
Q6_1   0.97 -0.32 0.59 0.41 1.2
Q6_2   0.93 -0.27 0.58 0.42 1.2
Q6_3   0.93 -0.26 0.59 0.41 1.2
Q6_4   0.91 -0.32 0.50 0.50 1.3
Q6_5   0.45  0.13 0.30 0.70 1.2
Q6_6   0.94 -0.17 0.68 0.32 1.1
Q6_7   0.95 -0.16 0.72 0.28 1.1
Q6_8   0.95 -0.21 0.65 0.35 1.1
Q6_9   0.26  0.35 0.31 0.69 1.9
Q6_10  0.28  0.37 0.37 0.63 1.9
Q6_11  0.38  0.41 0.54 0.46 2.0
Q7_1   0.43  0.43 0.64 0.36 2.0
Q7_2   0.21  0.57 0.54 0.46 1.3
Q7_3  -0.27  0.88 0.50 0.50 1.2
Q7_4   0.10  0.60 0.45 0.55 1.1
Q7_5   0.10  0.70 0.60 0.40 1.0
Q7_6   0.13  0.63 0.52 0.48 1.1
Q7_7  -0.40  1.06 0.67 0.33 1.3
Q7_8  -0.01  0.71 0.49 0.51 1.0
Q7_9   0.38  0.42 0.55 0.45 2.0
Q7_10  0.52  0.30 0.60 0.40 1.6
Q7_11  0.13  0.63 0.54 0.46 1.1
Q7_12 -0.15  0.74 0.41 0.59 1.1
Q7_13 -0.36  0.65 0.21 0.79 1.6
Q7_14 -0.46  0.91 0.43 0.57 1.5
Q7_15  0.40  0.36 0.50 0.50 2.0

                        PA1   PA2
SS loadings           14.67 14.42
Proportion Var         0.26  0.25
Cumulative Var         0.26  0.51
Proportion Explained   0.50  0.50
Cumulative Proportion  0.50  1.00

 With factor correlations of 
     PA1  PA2
PA1 1.00 0.72
PA2 0.72 1.00

Mean item complexity =  1.5
Test of the hypothesis that 2 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1483  and the objective function was  48.88 

The root mean square of the residuals (RMSR) is  0.07 
The df corrected root mean square of the residuals is  0.07 

Fit based upon off diagonal values = 0.98

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA2   
Q4_1   0.409  0.329
Q4_2   0.434  0.363
Q4_3   0.356  0.387
Q4_4   0.332  0.480
Q4_5   0.518       
Q4_6          0.480
Q4_7          0.549
Q4_8   0.577       
Q4_9   0.383  0.319
Q4_10  0.361  0.420
Q4_11  0.459  0.372
Q4_12  0.696       
Q4_13  0.802       
Q4_14  0.512       
Q4_15  0.541       
Q4_16  0.567       
Q4_17  0.543       
Q4_18  0.514  0.350
Q4_19  0.452  0.388
Q5_1          0.501
Q5_2          0.484
Q5_3   0.302  0.421
Q5_4          0.766
Q5_5          0.751
Q5_6          0.638
Q5_7   0.428       
Q5_8          0.609
Q5_9   0.438  0.385
Q5_10  0.343  0.359
Q5_11         0.508
Q5_12         0.528
Q6_1   0.969 -0.320
Q6_2   0.930       
Q6_3   0.930       
Q6_4   0.906 -0.323
Q6_5   0.447       
Q6_6   0.944       
Q6_7   0.955       
Q6_8   0.948       
Q6_9          0.345
Q6_10         0.370
Q6_11  0.382  0.410
Q7_1   0.430  0.431
Q7_2          0.570
Q7_3          0.879
Q7_4          0.596
Q7_5          0.701
Q7_6          0.627
Q7_7  -0.402  1.058
Q7_8          0.707
Q7_9   0.381  0.421
Q7_10  0.524  0.305
Q7_11         0.633
Q7_12         0.738
Q7_13 -0.358  0.646
Q7_14 -0.460  0.909
Q7_15  0.398  0.361

                  PA1    PA2
SS loadings    13.541 13.290
Proportion Var  0.238  0.233
Cumulative Var  0.238  0.471

fit <- psych::fa(r = cov.dat, nfactors = 2, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 2, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA2   h2   u2   H2   U2
Q4_1   0.48  0.11 0.31 0.44 0.41 0.59
Q4_2   0.49  0.10 0.32 0.35 0.48 0.52
Q4_3   0.42  0.15 0.29 0.41 0.42 0.58
Q4_4   0.37  0.25 0.33 0.34 0.49 0.51
Q4_5   0.55  0.08 0.37 0.40 0.48 0.52
Q4_6   0.33  0.36 0.41 0.55 0.42 0.58
Q4_7   0.08  0.48 0.29 0.59 0.33 0.67
Q4_8   0.67 -0.04 0.42 0.44 0.48 0.52
Q4_9   0.53  0.12 0.39 0.63 0.38 0.62
Q4_10  0.35  0.20 0.27 0.35 0.43 0.57
Q4_11  0.58  0.16 0.49 0.42 0.54 0.46
Q4_12  0.79 -0.08 0.54 0.57 0.49 0.51
Q4_13  0.72 -0.20 0.36 0.41 0.46 0.54
Q4_14  0.53  0.13 0.39 0.41 0.49 0.51
Q4_15  0.63  0.07 0.47 0.38 0.55 0.45
Q4_16  0.60  0.06 0.41 0.48 0.46 0.54
Q4_17  0.65 -0.01 0.41 0.52 0.44 0.56
Q4_18  0.56  0.08 0.39 0.29 0.58 0.42
Q4_19  0.58  0.18 0.51 0.43 0.55 0.45
Q5_1   0.32  0.35 0.38 0.52 0.42 0.58
Q5_2   0.22  0.50 0.46 0.62 0.43 0.57
Q5_3   0.36  0.37 0.46 0.64 0.42 0.58
Q5_4  -0.11  0.81 0.53 0.69 0.44 0.56
Q5_5  -0.19  0.77 0.41 0.66 0.39 0.61
Q5_6   0.15  0.54 0.42 0.40 0.52 0.48
Q5_7   0.39  0.25 0.35 0.54 0.39 0.61
Q5_8   0.17  0.60 0.53 0.58 0.48 0.52
Q5_9   0.48  0.30 0.52 0.47 0.53 0.47
Q5_10  0.29  0.26 0.26 0.44 0.37 0.63
Q5_11  0.35  0.34 0.40 0.50 0.44 0.56
Q5_12  0.22  0.46 0.41 0.50 0.45 0.55
Q6_1   0.70 -0.26 0.30 0.41 0.42 0.58
Q6_2   0.73 -0.20 0.37 0.46 0.44 0.56
Q6_3   0.71 -0.19 0.35 0.50 0.41 0.59
Q6_4   0.70 -0.23 0.32 0.54 0.37 0.63
Q6_5   0.44  0.08 0.25 0.81 0.24 0.76
Q6_6   0.71 -0.17 0.36 0.31 0.53 0.47
Q6_7   0.78 -0.17 0.45 0.31 0.59 0.41
Q6_8   0.79 -0.22 0.44 0.38 0.53 0.47
Q6_9   0.41  0.26 0.39 1.11 0.26 0.74
Q6_10  0.32  0.26 0.28 0.55 0.34 0.66
Q6_11  0.38  0.36 0.47 0.47 0.50 0.50
Q7_1   0.43  0.31 0.47 0.35 0.57 0.43
Q7_2   0.20  0.44 0.37 0.37 0.50 0.50
Q7_3  -0.20  0.85 0.52 0.50 0.51 0.49
Q7_4   0.15  0.52 0.40 0.56 0.42 0.58
Q7_5   0.19  0.55 0.49 0.40 0.55 0.45
Q7_6   0.19  0.49 0.41 0.44 0.48 0.52
Q7_7  -0.23  0.92 0.59 0.44 0.58 0.42
Q7_8   0.10  0.51 0.34 0.43 0.44 0.56
Q7_9   0.46  0.29 0.49 0.50 0.50 0.50
Q7_10  0.59  0.13 0.47 0.42 0.52 0.48
Q7_11  0.18  0.43 0.33 0.38 0.47 0.53
Q7_12 -0.02  0.63 0.38 0.66 0.37 0.63
Q7_13 -0.20  0.52 0.16 0.82 0.17 0.83
Q7_14 -0.32  0.82 0.40 0.57 0.41 0.59
Q7_15  0.43  0.21 0.36 0.46 0.44 0.56

                        PA1  PA2
SS loadings           13.13 9.53
Proportion Var         0.26 0.19
Cumulative Var         0.26 0.45
Proportion Explained   0.58 0.42
Cumulative Proportion  0.58 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA2   h2   u2
Q4_1     1  0.55  0.13 0.41 0.59
Q4_2     2  0.60  0.12 0.48 0.52
Q4_3     3  0.50  0.18 0.42 0.58
Q4_4     4  0.45  0.31 0.49 0.51
Q4_5     5  0.63  0.09 0.48 0.52
Q4_6     6  0.34  0.37 0.42 0.58
Q4_7     7  0.08  0.51 0.33 0.67
Q4_8     8  0.72 -0.04 0.48 0.52
Q4_9     9  0.53  0.11 0.38 0.62
Q4_10   10  0.45  0.26 0.43 0.57
Q4_11   11  0.61  0.16 0.54 0.46
Q4_12   12  0.75 -0.08 0.49 0.51
Q4_13   13  0.82 -0.23 0.46 0.54
Q4_14   14  0.59  0.15 0.49 0.51
Q4_15   15  0.69  0.08 0.55 0.45
Q4_16   16  0.64  0.06 0.46 0.54
Q4_17   17  0.67 -0.01 0.44 0.56
Q4_18   18  0.69  0.10 0.58 0.42
Q4_19   19  0.60  0.19 0.55 0.45
Q5_1    20  0.33  0.37 0.42 0.58
Q5_2    21  0.22  0.48 0.43 0.57
Q5_3    22  0.35  0.35 0.42 0.58
Q5_4    23 -0.10  0.73 0.44 0.56
Q5_5    24 -0.19  0.74 0.39 0.61
Q5_6    25  0.16  0.59 0.52 0.48
Q5_7    26  0.41  0.26 0.39 0.61
Q5_8    27  0.16  0.57 0.48 0.52
Q5_9    28  0.48  0.30 0.53 0.47
Q5_10   29  0.35  0.31 0.37 0.63
Q5_11   30  0.36  0.36 0.44 0.56
Q5_12   31  0.23  0.49 0.45 0.55
Q6_1    32  0.83 -0.31 0.42 0.58
Q6_2    33  0.80 -0.22 0.44 0.56
Q6_3    34  0.77 -0.21 0.41 0.59
Q6_4    35  0.76 -0.25 0.37 0.63
Q6_5    36  0.43  0.08 0.24 0.76
Q6_6    37  0.86 -0.20 0.53 0.47
Q6_7    38  0.89 -0.20 0.59 0.41
Q6_8    39  0.88 -0.24 0.53 0.47
Q6_9    40  0.33  0.22 0.26 0.74
Q6_10   41  0.35  0.28 0.34 0.66
Q6_11   42  0.39  0.37 0.50 0.50
Q7_1    43  0.47  0.34 0.57 0.43
Q7_2    44  0.24  0.52 0.50 0.50
Q7_3    45 -0.19  0.84 0.51 0.49
Q7_4    46  0.15  0.53 0.42 0.58
Q7_5    47  0.20  0.58 0.55 0.45
Q7_6    48  0.20  0.54 0.48 0.52
Q7_7    49 -0.23  0.90 0.58 0.42
Q7_8    50  0.12  0.58 0.44 0.56
Q7_9    51  0.47  0.29 0.50 0.50
Q7_10   52  0.62  0.13 0.52 0.48
Q7_11   53  0.22  0.51 0.47 0.53
Q7_12   54 -0.02  0.62 0.37 0.63
Q7_13   55 -0.21  0.53 0.17 0.83
Q7_14   56 -0.32  0.83 0.41 0.59
Q7_15   57  0.48  0.23 0.44 0.56

                  PA1   PA2
SS loadings     14.74 10.70
Proportion Var   0.26  0.19
Cumulative Var   0.26  0.45
Cum. factor Var  0.58  1.00

 With factor correlations of 
     PA1  PA2
PA1 1.00 0.71
PA2 0.71 1.00

Mean item complexity =  1.3
Test of the hypothesis that 2 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1483  and the objective function was  15.97 

The root mean square of the residuals (RMSR) is  0.06 
The df corrected root mean square of the residuals is  0.06 

Fit based upon off diagonal values = 0.97
Measures of factor score adequacy             
                                                   PA1  PA2
Correlation of (regression) scores with factors   0.98 0.97
Multiple R square of scores with factors          0.97 0.95
Minimum correlation of possible factor scores     0.94 0.90

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA2   
Q4_1   0.476       
Q4_2   0.492       
Q4_3   0.420       
Q4_4   0.368       
Q4_5   0.554       
Q4_6   0.332  0.358
Q4_7          0.478
Q4_8   0.671       
Q4_9   0.534       
Q4_10  0.355       
Q4_11  0.583       
Q4_12  0.789       
Q4_13  0.720       
Q4_14  0.526       
Q4_15  0.629       
Q4_16  0.597       
Q4_17  0.647       
Q4_18  0.564       
Q4_19  0.578       
Q5_1   0.316  0.354
Q5_2          0.498
Q5_3   0.362  0.370
Q5_4          0.806
Q5_5          0.766
Q5_6          0.539
Q5_7   0.390       
Q5_8          0.602
Q5_9   0.482       
Q5_10              
Q5_11  0.346  0.341
Q5_12         0.463
Q6_1   0.698       
Q6_2   0.734       
Q6_3   0.712       
Q6_4   0.701       
Q6_5   0.441       
Q6_6   0.705       
Q6_7   0.782       
Q6_8   0.795       
Q6_9   0.405       
Q6_10  0.319       
Q6_11  0.383  0.361
Q7_1   0.427  0.310
Q7_2          0.444
Q7_3          0.849
Q7_4          0.521
Q7_5          0.554
Q7_6          0.493
Q7_7          0.918
Q7_8          0.507
Q7_9   0.463       
Q7_10  0.589       
Q7_11         0.430
Q7_12         0.633
Q7_13         0.522
Q7_14 -0.315  0.817
Q7_15  0.431       

                  PA1   PA2
SS loadings    12.383 8.785
Proportion Var  0.217 0.154
Cumulative Var  0.217 0.371

Three factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 3, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 3, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA1   PA2   PA3   h2   u2 com
Q4_1   1.00 -0.07 -0.20 0.66 0.34 1.1
Q4_2   0.99 -0.03 -0.17 0.72 0.28 1.1
Q4_3   0.98 -0.01 -0.24 0.66 0.34 1.1
Q4_4   0.85  0.14 -0.19 0.69 0.31 1.2
Q4_5   0.68  0.02  0.09 0.58 0.42 1.0
Q4_6   0.29  0.38  0.08 0.47 0.53 2.0
Q4_7   0.04  0.54  0.03 0.35 0.65 1.0
Q4_8   0.97 -0.20 -0.02 0.68 0.32 1.1
Q4_9   0.74  0.03 -0.07 0.50 0.50 1.0
Q4_10  0.74  0.13 -0.09 0.60 0.40 1.1
Q4_11  0.72  0.10  0.01 0.65 0.35 1.0
Q4_12  0.43 -0.05  0.41 0.56 0.44 2.0
Q4_13  0.60 -0.25  0.41 0.59 0.41 2.2
Q4_14  0.48  0.12  0.21 0.55 0.45 1.5
Q4_15  0.77  0.00  0.06 0.67 0.33 1.0
Q4_16  0.66 -0.05  0.15 0.56 0.44 1.1
Q4_17  0.75 -0.09  0.08 0.55 0.45 1.1
Q4_18  1.04 -0.06 -0.12 0.83 0.17 1.0
Q4_19  0.73  0.11  0.00 0.67 0.33 1.0
Q5_1   0.38  0.36  0.00 0.48 0.52 2.0
Q5_2   0.07  0.48  0.17 0.44 0.56 1.3
Q5_3   0.21  0.36  0.17 0.45 0.55 2.1
Q5_4   0.00  0.75 -0.15 0.44 0.56 1.1
Q5_5   0.02  0.72 -0.22 0.37 0.63 1.2
Q5_6   0.16  0.58  0.03 0.54 0.46 1.2
Q5_7  -0.05  0.35  0.45 0.48 0.52 1.9
Q5_8  -0.01  0.63  0.13 0.52 0.48 1.1
Q5_9   0.21  0.34  0.30 0.59 0.41 2.6
Q5_10  0.21  0.30  0.21 0.43 0.57 2.6
Q5_11  0.22  0.44  0.11 0.50 0.50 1.6
Q5_12  0.04  0.54  0.17 0.49 0.51 1.2
Q6_1  -0.06 -0.21  0.98 0.67 0.33 1.1
Q6_2  -0.21 -0.10  1.05 0.72 0.28 1.1
Q6_3  -0.19 -0.10  1.03 0.72 0.28 1.1
Q6_4  -0.18 -0.17  1.00 0.61 0.39 1.1
Q6_5   0.03  0.16  0.42 0.32 0.68 1.3
Q6_6   0.01 -0.09  0.91 0.74 0.26 1.0
Q6_7   0.08 -0.10  0.88 0.76 0.24 1.0
Q6_8  -0.08 -0.09  0.98 0.74 0.26 1.0
Q6_9   0.02  0.37  0.24 0.33 0.67 1.7
Q6_10  0.02  0.39  0.26 0.39 0.61 1.7
Q6_11 -0.04  0.47  0.40 0.59 0.41 2.0
Q7_1   0.11  0.43  0.35 0.66 0.34 2.1
Q7_2   0.04  0.58  0.18 0.56 0.44 1.2
Q7_3  -0.24  0.98 -0.11 0.57 0.43 1.2
Q7_4  -0.07  0.65  0.14 0.48 0.52 1.1
Q7_5   0.11  0.67  0.04 0.61 0.39 1.1
Q7_6   0.04  0.63  0.11 0.54 0.46 1.1
Q7_7  -0.05  1.05 -0.35 0.68 0.32 1.2
Q7_8   0.10  0.67 -0.06 0.50 0.50 1.1
Q7_9   0.29  0.33  0.20 0.55 0.45 2.6
Q7_10  0.38  0.19  0.28 0.60 0.40 2.4
Q7_11  0.25  0.54 -0.02 0.54 0.46 1.4
Q7_12 -0.06  0.76 -0.10 0.43 0.57 1.0
Q7_13 -0.23  0.72 -0.20 0.24 0.76 1.4
Q7_14 -0.21  0.97 -0.31 0.46 0.54 1.3
Q7_15  0.28  0.28  0.22 0.50 0.50 2.9

                        PA1   PA2  PA3
SS loadings           11.98 11.37 8.44
Proportion Var         0.21  0.20 0.15
Cumulative Var         0.21  0.41 0.56
Proportion Explained   0.38  0.36 0.27
Cumulative Proportion  0.38  0.73 1.00

 With factor correlations of 
     PA1  PA2  PA3
PA1 1.00 0.74 0.73
PA2 0.74 1.00 0.68
PA3 0.73 0.68 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1428  and the objective function was  44.36 

The root mean square of the residuals (RMSR) is  0.05 
The df corrected root mean square of the residuals is  0.06 

Fit based upon off diagonal values = 0.99

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA2    PA3   
Q4_1   0.997              
Q4_2   0.990              
Q4_3   0.982              
Q4_4   0.854              
Q4_5   0.680              
Q4_6          0.380       
Q4_7          0.543       
Q4_8   0.970              
Q4_9   0.737              
Q4_10  0.739              
Q4_11  0.721              
Q4_12  0.431         0.411
Q4_13  0.595         0.415
Q4_14  0.476              
Q4_15  0.770              
Q4_16  0.664              
Q4_17  0.747              
Q4_18  1.039              
Q4_19  0.727              
Q5_1   0.379  0.361       
Q5_2          0.479       
Q5_3          0.365       
Q5_4          0.754       
Q5_5          0.724       
Q5_6          0.583       
Q5_7          0.349  0.446
Q5_8          0.635       
Q5_9          0.342  0.302
Q5_10         0.304       
Q5_11         0.440       
Q5_12         0.539       
Q6_1                 0.985
Q6_2                 1.050
Q6_3                 1.033
Q6_4                 1.000
Q6_5                 0.415
Q6_6                 0.914
Q6_7                 0.880
Q6_8                 0.979
Q6_9          0.369       
Q6_10         0.395       
Q6_11         0.473  0.395
Q7_1          0.431  0.350
Q7_2          0.581       
Q7_3          0.981       
Q7_4          0.648       
Q7_5          0.673       
Q7_6          0.632       
Q7_7          1.051 -0.349
Q7_8          0.670       
Q7_9          0.335       
Q7_10  0.381              
Q7_11         0.540       
Q7_12         0.762       
Q7_13         0.721       
Q7_14         0.969 -0.312
Q7_15                     

                  PA1    PA2   PA3
SS loadings    11.797 11.310 8.941
Proportion Var  0.207  0.198 0.157
Cumulative Var  0.207  0.405 0.562

fit <- psych::fa(r = cov.dat, nfactors = 3, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 3, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA2   PA1   PA3   h2   u2   H2   U2
Q4_1  -0.05  0.80 -0.17 0.42 0.33 0.57 0.43
Q4_2  -0.05  0.78 -0.15 0.43 0.25 0.63 0.37
Q4_3   0.00  0.76 -0.20 0.40 0.30 0.57 0.43
Q4_4   0.14  0.63 -0.16 0.39 0.27 0.59 0.41
Q4_5  -0.01  0.60  0.06 0.40 0.37 0.52 0.48
Q4_6   0.35  0.27  0.08 0.41 0.56 0.42 0.58
Q4_7   0.50  0.06 -0.01 0.29 0.59 0.33 0.67
Q4_8  -0.20  0.87 -0.03 0.52 0.34 0.61 0.39
Q4_9  -0.02  0.76 -0.09 0.47 0.54 0.46 0.54
Q4_10  0.11  0.55 -0.11 0.31 0.31 0.50 0.50
Q4_11  0.05  0.71 -0.01 0.55 0.37 0.60 0.40
Q4_12 -0.11  0.51  0.36 0.54 0.57 0.49 0.51
Q4_13 -0.25  0.54  0.29 0.36 0.41 0.47 0.53
Q4_14  0.09  0.47  0.13 0.40 0.40 0.50 0.50
Q4_15 -0.04  0.72  0.03 0.52 0.32 0.62 0.38
Q4_16 -0.03  0.62  0.09 0.44 0.45 0.49 0.51
Q4_17 -0.13  0.73  0.06 0.46 0.47 0.49 0.51
Q4_18 -0.07  0.83 -0.11 0.50 0.18 0.73 0.27
Q4_19  0.06  0.75 -0.04 0.58 0.36 0.62 0.38
Q5_1   0.32  0.35 -0.01 0.39 0.51 0.43 0.57
Q5_2   0.54  0.06  0.13 0.46 0.61 0.43 0.57
Q5_3   0.38  0.22  0.15 0.46 0.64 0.42 0.58
Q5_4   0.85 -0.06 -0.13 0.53 0.69 0.44 0.56
Q5_5   0.79 -0.06 -0.20 0.41 0.66 0.38 0.62
Q5_6   0.56  0.10  0.02 0.42 0.40 0.52 0.48
Q5_7   0.32 -0.01  0.37 0.38 0.50 0.43 0.57
Q5_8   0.67 -0.02  0.13 0.55 0.56 0.50 0.50
Q5_9   0.33  0.21  0.28 0.53 0.46 0.53 0.47
Q5_10  0.27  0.16  0.13 0.26 0.44 0.37 0.63
Q5_11  0.34  0.24  0.11 0.40 0.50 0.44 0.56
Q5_12  0.51  0.05  0.14 0.41 0.49 0.46 0.54
Q6_1  -0.17 -0.04  0.75 0.39 0.32 0.55 0.45
Q6_2  -0.08 -0.16  0.89 0.55 0.28 0.66 0.34
Q6_3  -0.07 -0.18  0.88 0.53 0.33 0.62 0.38
Q6_4  -0.12 -0.13  0.84 0.46 0.40 0.54 0.46
Q6_5   0.13  0.06  0.37 0.27 0.80 0.25 0.75
Q6_6  -0.09  0.03  0.69 0.43 0.24 0.64 0.36
Q6_7  -0.10  0.10  0.71 0.51 0.25 0.67 0.33
Q6_8  -0.12  0.00  0.82 0.54 0.27 0.67 0.33
Q6_9   0.30  0.14  0.25 0.39 1.10 0.26 0.74
Q6_10  0.30  0.07  0.23 0.29 0.54 0.35 0.65
Q6_11  0.44  0.00  0.34 0.51 0.43 0.54 0.46
Q7_1   0.35  0.13  0.29 0.48 0.33 0.59 0.41
Q7_2   0.49  0.05  0.12 0.37 0.36 0.51 0.49
Q7_3   0.92 -0.20 -0.10 0.54 0.49 0.53 0.47
Q7_4   0.58 -0.03  0.13 0.42 0.54 0.44 0.56
Q7_5   0.57  0.14  0.03 0.50 0.40 0.55 0.45
Q7_6   0.53  0.06  0.09 0.41 0.43 0.49 0.51
Q7_7   0.94 -0.03 -0.27 0.59 0.44 0.57 0.43
Q7_8   0.52  0.12 -0.04 0.34 0.43 0.44 0.56
Q7_9   0.29  0.31  0.18 0.49 0.50 0.50 0.50
Q7_10  0.12  0.37  0.26 0.47 0.43 0.52 0.48
Q7_11  0.42  0.20 -0.02 0.33 0.38 0.47 0.53
Q7_12  0.67 -0.02 -0.05 0.39 0.66 0.37 0.63
Q7_13  0.56 -0.16 -0.11 0.17 0.81 0.17 0.83
Q7_14  0.87 -0.19 -0.21 0.40 0.57 0.42 0.58
Q7_15  0.21  0.28  0.18 0.36 0.46 0.44 0.56

                       PA2  PA1  PA3
SS loadings           9.48 9.40 5.85
Proportion Var        0.19 0.19 0.12
Cumulative Var        0.19 0.37 0.49
Proportion Explained  0.38 0.38 0.24
Cumulative Proportion 0.38 0.76 1.00

 Standardized loadings (pattern matrix)
      item   PA2   PA1   PA3   h2   u2
Q4_1     1 -0.05  0.92 -0.20 0.57 0.43
Q4_2     2 -0.06  0.96 -0.18 0.63 0.37
Q4_3     3  0.00  0.91 -0.24 0.57 0.43
Q4_4     4  0.17  0.78 -0.20 0.59 0.41
Q4_5     5 -0.01  0.68  0.07 0.52 0.48
Q4_6     6  0.36  0.27  0.08 0.42 0.58
Q4_7     7  0.53  0.06 -0.01 0.33 0.67
Q4_8     8 -0.21  0.94 -0.03 0.61 0.39
Q4_9     9 -0.02  0.76 -0.09 0.46 0.54
Q4_10   10  0.14  0.69 -0.13 0.50 0.50
Q4_11   11  0.05  0.75 -0.01 0.60 0.40
Q4_12   12 -0.11  0.49  0.35 0.49 0.51
Q4_13   13 -0.29  0.61  0.33 0.47 0.53
Q4_14   14  0.10  0.52  0.14 0.50 0.50
Q4_15   15 -0.04  0.79  0.04 0.62 0.38
Q4_16   16 -0.03  0.66  0.09 0.49 0.51
Q4_17   17 -0.13  0.75  0.06 0.49 0.51
Q4_18   18 -0.08  1.01 -0.13 0.73 0.27
Q4_19   19  0.06  0.77 -0.05 0.62 0.38
Q5_1    20  0.34  0.37 -0.01 0.43 0.57
Q5_2    21  0.52  0.06  0.12 0.43 0.57
Q5_3    22  0.37  0.21  0.14 0.42 0.58
Q5_4    23  0.76 -0.05 -0.11 0.44 0.56
Q5_5    24  0.77 -0.06 -0.19 0.38 0.62
Q5_6    25  0.62  0.11  0.02 0.52 0.48
Q5_7    26  0.34 -0.01  0.39 0.43 0.57
Q5_8    27  0.63 -0.02  0.12 0.50 0.50
Q5_9    28  0.33  0.21  0.28 0.53 0.47
Q5_10   29  0.32  0.19  0.16 0.37 0.63
Q5_11   30  0.36  0.26  0.12 0.44 0.56
Q5_12   31  0.53  0.05  0.14 0.46 0.54
Q6_1    32 -0.20 -0.05  0.89 0.55 0.45
Q6_2    33 -0.09 -0.18  0.98 0.66 0.34
Q6_3    34 -0.08 -0.19  0.95 0.62 0.38
Q6_4    35 -0.13 -0.14  0.90 0.54 0.46
Q6_5    36  0.13  0.06  0.36 0.25 0.75
Q6_6    37 -0.11  0.04  0.84 0.64 0.36
Q6_7    38 -0.11  0.11  0.81 0.67 0.33
Q6_8    39 -0.14 -0.01  0.90 0.67 0.33
Q6_9    40  0.25  0.12  0.21 0.26 0.74
Q6_10   41  0.33  0.07  0.26 0.35 0.65
Q6_11   42  0.45  0.00  0.35 0.54 0.46
Q7_1    43  0.39  0.14  0.32 0.59 0.41
Q7_2    44  0.57  0.05  0.14 0.51 0.49
Q7_3    45  0.91 -0.20 -0.10 0.53 0.47
Q7_4    46  0.59 -0.03  0.13 0.44 0.56
Q7_5    47  0.61  0.14  0.03 0.55 0.45
Q7_6    48  0.57  0.07  0.10 0.49 0.51
Q7_7    49  0.93 -0.03 -0.27 0.57 0.43
Q7_8    50  0.59  0.14 -0.04 0.44 0.56
Q7_9    51  0.29  0.32  0.18 0.50 0.50
Q7_10   52  0.12  0.40  0.28 0.52 0.48
Q7_11   53  0.50  0.24 -0.02 0.47 0.53
Q7_12   54  0.65 -0.02 -0.05 0.37 0.63
Q7_13   55  0.57 -0.16 -0.12 0.17 0.83
Q7_14   56  0.88 -0.20 -0.22 0.42 0.58
Q7_15   57  0.23  0.30  0.20 0.44 0.56

                  PA2   PA1  PA3
SS loadings     10.65 10.55 6.57
Proportion Var   0.19  0.19 0.12
Cumulative Var   0.19  0.37 0.49
Cum. factor Var  0.38  0.76 1.00

 With factor correlations of 
     PA2  PA1  PA3
PA2 1.00 0.74 0.65
PA1 0.74 1.00 0.72
PA3 0.65 0.72 1.00

Mean item complexity =  1.4
Test of the hypothesis that 3 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1428  and the objective function was  12.51 

The root mean square of the residuals (RMSR) is  0.05 
The df corrected root mean square of the residuals is  0.05 

Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   PA2  PA1  PA3
Correlation of (regression) scores with factors   0.98 0.98 0.98
Multiple R square of scores with factors          0.95 0.97 0.95
Minimum correlation of possible factor scores     0.90 0.93 0.90

print(fit$loadings, cutoff=0.3)

Loadings:
      PA2    PA1    PA3   
Q4_1          0.796       
Q4_2          0.784       
Q4_3          0.758       
Q4_4          0.633       
Q4_5          0.596       
Q4_6   0.349              
Q4_7   0.497              
Q4_8          0.875       
Q4_9          0.764       
Q4_10         0.548       
Q4_11         0.712       
Q4_12         0.512  0.364
Q4_13         0.538       
Q4_14         0.470       
Q4_15         0.724       
Q4_16         0.616       
Q4_17         0.727       
Q4_18         0.827       
Q4_19         0.748       
Q5_1   0.322  0.352       
Q5_2   0.540              
Q5_3   0.382              
Q5_4   0.846              
Q5_5   0.792              
Q5_6   0.560              
Q5_7   0.322         0.368
Q5_8   0.667              
Q5_9   0.327              
Q5_10                     
Q5_11  0.341              
Q5_12  0.507              
Q6_1                 0.751
Q6_2                 0.893
Q6_3                 0.881
Q6_4                 0.837
Q6_5                 0.372
Q6_6                 0.688
Q6_7                 0.709
Q6_8                 0.815
Q6_9   0.301              
Q6_10  0.300              
Q6_11  0.439         0.343
Q7_1   0.354              
Q7_2   0.486              
Q7_3   0.923              
Q7_4   0.581              
Q7_5   0.574              
Q7_6   0.528              
Q7_7   0.938              
Q7_8   0.516              
Q7_9          0.313       
Q7_10         0.374       
Q7_11  0.422              
Q7_12  0.670              
Q7_13  0.564              
Q7_14  0.867              
Q7_15                     

                 PA2   PA1   PA3
SS loadings    9.482 9.219 6.036
Proportion Var 0.166 0.162 0.106
Cumulative Var 0.166 0.328 0.434

Four factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 4, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 4, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA1   PA3   PA2   PA4   h2   u2 com
Q4_1   0.99 -0.20 -0.09  0.02 0.66 0.34 1.1
Q4_2   0.99 -0.18 -0.06  0.04 0.72 0.28 1.1
Q4_3   0.98 -0.25 -0.02  0.01 0.66 0.34 1.1
Q4_4   0.86 -0.19  0.13  0.00 0.69 0.31 1.1
Q4_5   0.67  0.08 -0.09  0.14 0.59 0.41 1.2
Q4_6   0.27  0.06  0.15  0.30 0.48 0.52 2.6
Q4_7   0.03  0.02  0.33  0.28 0.35 0.65 2.0
Q4_8   0.98 -0.01 -0.13 -0.10 0.68 0.32 1.1
Q4_9   0.76 -0.06  0.13 -0.13 0.52 0.48 1.1
Q4_10  0.75 -0.09  0.15 -0.04 0.61 0.39 1.1
Q4_11  0.74  0.02  0.13 -0.05 0.66 0.34 1.1
Q4_12  0.44  0.42  0.03 -0.12 0.57 0.43 2.2
Q4_13  0.60  0.42 -0.17 -0.10 0.59 0.41 2.1
Q4_14  0.48  0.21  0.10  0.02 0.56 0.44 1.5
Q4_15  0.76  0.06 -0.06  0.08 0.67 0.33 1.0
Q4_16  0.64  0.13 -0.23  0.24 0.59 0.41 1.6
Q4_17  0.76  0.09 -0.01 -0.12 0.56 0.44 1.1
Q4_18  1.03 -0.13 -0.11  0.06 0.83 0.17 1.1
Q4_19  0.74  0.01  0.12 -0.02 0.67 0.33 1.1
Q5_1   0.35 -0.02  0.08  0.36 0.50 0.50 2.1
Q5_2   0.02  0.13  0.00  0.64 0.55 0.45 1.1
Q5_3   0.14  0.12 -0.15  0.69 0.61 0.39 1.2
Q5_4  -0.09 -0.23  0.10  0.93 0.67 0.33 1.2
Q5_5  -0.06 -0.30  0.09  0.90 0.59 0.41 1.3
Q5_6   0.09 -0.03  0.00  0.80 0.71 0.29 1.0
Q5_7  -0.07  0.43  0.11  0.30 0.49 0.51 2.0
Q5_8  -0.08  0.08  0.08  0.75 0.65 0.35 1.1
Q5_9   0.16  0.27 -0.05  0.52 0.66 0.34 1.8
Q5_10  0.19  0.19  0.03  0.35 0.45 0.55 2.1
Q5_11  0.21  0.10  0.25  0.24 0.50 0.50 3.3
Q5_12  0.01  0.15  0.21  0.43 0.51 0.49 1.8
Q6_1  -0.07  0.98 -0.19 -0.03 0.67 0.33 1.1
Q6_2  -0.22  1.05 -0.16  0.07 0.72 0.28 1.1
Q6_3  -0.20  1.03 -0.16  0.07 0.72 0.28 1.1
Q6_4  -0.18  1.00 -0.19  0.02 0.61 0.39 1.1
Q6_5   0.04  0.43  0.18 -0.04 0.32 0.68 1.4
Q6_6   0.02  0.93 -0.02 -0.11 0.75 0.25 1.0
Q6_7   0.09  0.90  0.02 -0.17 0.78 0.22 1.1
Q6_8  -0.07  1.00  0.03 -0.18 0.77 0.23 1.1
Q6_9   0.06  0.28  0.53 -0.23 0.41 0.59 1.9
Q6_10  0.04  0.28  0.37  0.02 0.40 0.60 1.9
Q6_11 -0.03  0.40  0.38  0.11 0.59 0.41 2.2
Q7_1   0.11  0.35  0.28  0.18 0.66 0.34 2.7
Q7_2   0.06  0.19  0.49  0.10 0.57 0.43 1.4
Q7_3  -0.22 -0.09  0.89  0.11 0.60 0.40 1.2
Q7_4  -0.04  0.16  0.63  0.01 0.51 0.49 1.1
Q7_5   0.14  0.07  0.74 -0.10 0.68 0.32 1.1
Q7_6   0.07  0.13  0.66 -0.05 0.59 0.41 1.1
Q7_7  -0.02 -0.33  0.96  0.12 0.72 0.28 1.3
Q7_8   0.13 -0.04  0.70 -0.05 0.55 0.45 1.1
Q7_9   0.30  0.20  0.27  0.07 0.56 0.44 2.9
Q7_10  0.39  0.28  0.17  0.02 0.60 0.40 2.3
Q7_11  0.28  0.00  0.57 -0.05 0.58 0.42 1.5
Q7_12 -0.03 -0.07  0.79 -0.04 0.49 0.51 1.0
Q7_13 -0.19 -0.17  0.82 -0.12 0.32 0.68 1.3
Q7_14 -0.19 -0.30  0.83  0.17 0.48 0.52 1.5
Q7_15  0.29  0.22  0.23  0.05 0.50 0.50 2.9

                        PA1  PA3  PA2  PA4
SS loadings           11.90 8.39 7.74 5.64
Proportion Var         0.21 0.15 0.14 0.10
Cumulative Var         0.21 0.36 0.49 0.59
Proportion Explained   0.35 0.25 0.23 0.17
Cumulative Proportion  0.35 0.60 0.83 1.00

 With factor correlations of 
     PA1  PA3  PA2  PA4
PA1 1.00 0.74 0.70 0.67
PA3 0.74 1.00 0.64 0.63
PA2 0.70 0.64 1.00 0.68
PA4 0.67 0.63 0.68 1.00

Mean item complexity =  1.5
Test of the hypothesis that 4 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1374  and the objective function was  42.03 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

Fit based upon off diagonal values = 0.99

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA3    PA2    PA4   
Q4_1   0.994                     
Q4_2   0.987                     
Q4_3   0.983                     
Q4_4   0.863                     
Q4_5   0.668                     
Q4_6                        0.300
Q4_7                 0.325       
Q4_8   0.976                     
Q4_9   0.758                     
Q4_10  0.752                     
Q4_11  0.736                     
Q4_12  0.445  0.424              
Q4_13  0.599  0.418              
Q4_14  0.481                     
Q4_15  0.763                     
Q4_16  0.640                     
Q4_17  0.761                     
Q4_18  1.033                     
Q4_19  0.737                     
Q5_1   0.355                0.363
Q5_2                        0.639
Q5_3                        0.693
Q5_4                        0.929
Q5_5                        0.899
Q5_6                        0.796
Q5_7          0.433         0.304
Q5_8                        0.755
Q5_9                        0.519
Q5_10                       0.352
Q5_11                            
Q5_12                       0.427
Q6_1          0.984              
Q6_2          1.045              
Q6_3          1.028              
Q6_4          0.996              
Q6_5          0.427              
Q6_6          0.926              
Q6_7          0.901              
Q6_8          1.003              
Q6_9                 0.531       
Q6_10                0.370       
Q6_11         0.404  0.378       
Q7_1          0.349              
Q7_2                 0.491       
Q7_3                 0.890       
Q7_4                 0.625       
Q7_5                 0.740       
Q7_6                 0.660       
Q7_7         -0.333  0.957       
Q7_8                 0.703       
Q7_9   0.301                     
Q7_10  0.390                     
Q7_11                0.571       
Q7_12                0.791       
Q7_13                0.817       
Q7_14                0.832       
Q7_15                            

                  PA1   PA3   PA2   PA4
SS loadings    11.819 9.051 7.625 5.243
Proportion Var  0.207 0.159 0.134 0.092
Cumulative Var  0.207 0.366 0.500 0.592

fit <- psych::fa(r = cov.dat, nfactors = 4, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 4, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA3   PA2   PA4   h2   u2   H2   U2
Q4_1   0.81 -0.18 -0.09  0.03 0.43 0.32 0.57 0.43
Q4_2   0.79 -0.16 -0.07  0.01 0.43 0.25 0.63 0.37
Q4_3   0.77 -0.21 -0.02  0.02 0.40 0.30 0.57 0.43
Q4_4   0.64 -0.17  0.11  0.03 0.40 0.27 0.59 0.41
Q4_5   0.60  0.06 -0.09  0.08 0.41 0.37 0.52 0.48
Q4_6   0.27  0.08  0.13  0.26 0.41 0.55 0.43 0.57
Q4_7   0.06 -0.01  0.29  0.25 0.29 0.59 0.32 0.68
Q4_8   0.89 -0.03 -0.14 -0.09 0.52 0.34 0.61 0.39
Q4_9   0.78 -0.10  0.09 -0.14 0.48 0.53 0.48 0.52
Q4_10  0.56 -0.11  0.12 -0.01 0.32 0.31 0.51 0.49
Q4_11  0.73 -0.01  0.09 -0.07 0.55 0.36 0.60 0.40
Q4_12  0.52  0.37  0.01 -0.16 0.55 0.56 0.49 0.51
Q4_13  0.54  0.29 -0.17 -0.13 0.36 0.41 0.47 0.53
Q4_14  0.48  0.13  0.10 -0.02 0.40 0.40 0.50 0.50
Q4_15  0.73  0.03 -0.08  0.03 0.52 0.32 0.62 0.38
Q4_16  0.62  0.08 -0.21  0.19 0.46 0.42 0.52 0.48
Q4_17  0.74  0.05 -0.03 -0.14 0.46 0.47 0.50 0.50
Q4_18  0.84 -0.12 -0.10  0.02 0.50 0.18 0.73 0.27
Q4_19  0.76 -0.05  0.08 -0.04 0.58 0.36 0.62 0.38
Q5_1   0.35 -0.01  0.08  0.28 0.40 0.50 0.44 0.56
Q5_2   0.05  0.13  0.04  0.60 0.55 0.52 0.51 0.49
Q5_3   0.20  0.14 -0.14  0.61 0.58 0.51 0.53 0.47
Q5_4  -0.11 -0.16  0.09  0.97 0.78 0.45 0.64 0.36
Q5_5  -0.10 -0.23  0.08  0.91 0.63 0.44 0.59 0.41
Q5_6   0.08  0.01  0.01  0.66 0.54 0.28 0.65 0.35
Q5_7  -0.02  0.38  0.10  0.26 0.39 0.50 0.44 0.56
Q5_8  -0.05  0.13  0.08  0.71 0.67 0.45 0.60 0.40
Q5_9   0.20  0.29 -0.05  0.42 0.58 0.41 0.58 0.42
Q5_10  0.16  0.14  0.03  0.28 0.27 0.43 0.39 0.61
Q5_11  0.25  0.12  0.21  0.16 0.40 0.50 0.44 0.56
Q5_12  0.05  0.14  0.21  0.35 0.42 0.48 0.47 0.53
Q6_1  -0.05  0.76 -0.16 -0.04 0.39 0.32 0.55 0.45
Q6_2  -0.17  0.91 -0.13  0.03 0.55 0.28 0.66 0.34
Q6_3  -0.19  0.90 -0.14  0.05 0.53 0.33 0.62 0.38
Q6_4  -0.14  0.85 -0.17  0.02 0.46 0.40 0.54 0.46
Q6_5   0.07  0.38  0.19 -0.07 0.28 0.78 0.26 0.74
Q6_6   0.03  0.70 -0.03 -0.09 0.43 0.24 0.64 0.36
Q6_7   0.10  0.72  0.01 -0.15 0.52 0.24 0.68 0.32
Q6_8   0.00  0.84  0.01 -0.18 0.56 0.26 0.68 0.32
Q6_9   0.16  0.27  0.58 -0.31 0.52 0.97 0.35 0.65
Q6_10  0.07  0.24  0.32 -0.02 0.31 0.53 0.37 0.63
Q6_11  0.00  0.35  0.37  0.08 0.51 0.43 0.55 0.45
Q7_1   0.14  0.29  0.23  0.14 0.48 0.34 0.59 0.41
Q7_2   0.05  0.13  0.39  0.12 0.38 0.36 0.51 0.49
Q7_3  -0.20 -0.10  0.86  0.12 0.59 0.43 0.58 0.42
Q7_4  -0.02  0.13  0.56  0.04 0.44 0.52 0.46 0.54
Q7_5   0.15  0.04  0.66 -0.07 0.56 0.34 0.63 0.37
Q7_6   0.08  0.10  0.59 -0.05 0.46 0.38 0.55 0.45
Q7_7  -0.02 -0.28  0.90  0.11 0.65 0.38 0.63 0.37
Q7_8   0.13 -0.03  0.57 -0.04 0.39 0.38 0.50 0.50
Q7_9   0.32  0.18  0.23  0.06 0.49 0.50 0.50 0.50
Q7_10  0.38  0.27  0.11  0.00 0.47 0.42 0.52 0.48
Q7_11  0.22 -0.02  0.43  0.00 0.35 0.35 0.50 0.50
Q7_12 -0.01 -0.05  0.73 -0.03 0.46 0.59 0.44 0.56
Q7_13 -0.15 -0.12  0.73 -0.14 0.27 0.71 0.27 0.73
Q7_14 -0.19 -0.22  0.75  0.18 0.43 0.55 0.44 0.56
Q7_15  0.28  0.18  0.17  0.04 0.36 0.46 0.44 0.56

                       PA1  PA3  PA2  PA4
SS loadings           9.51 5.94 6.32 4.73
Proportion Var        0.19 0.12 0.12 0.09
Cumulative Var        0.19 0.30 0.43 0.52
Proportion Explained  0.36 0.22 0.24 0.18
Cumulative Proportion 0.36 0.58 0.82 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA3   PA2   PA4   h2   u2
Q4_1     1  0.93 -0.21 -0.10  0.04 0.57 0.43
Q4_2     2  0.97 -0.19 -0.08  0.01 0.63 0.37
Q4_3     3  0.92 -0.25 -0.02  0.02 0.57 0.43
Q4_4     4  0.79 -0.21  0.13  0.04 0.59 0.41
Q4_5     5  0.68  0.06 -0.10  0.09 0.52 0.48
Q4_6     6  0.28  0.08  0.13  0.26 0.43 0.57
Q4_7     7  0.07 -0.01  0.31  0.26 0.32 0.68
Q4_8     8  0.95 -0.04 -0.15 -0.09 0.61 0.39
Q4_9     9  0.78 -0.10  0.09 -0.14 0.48 0.52
Q4_10   10  0.71 -0.14  0.15 -0.01 0.51 0.49
Q4_11   11  0.76 -0.01  0.10 -0.07 0.60 0.40
Q4_12   12  0.50  0.35  0.01 -0.15 0.49 0.51
Q4_13   13  0.62  0.33 -0.19 -0.14 0.47 0.53
Q4_14   14  0.53  0.14  0.11 -0.02 0.50 0.50
Q4_15   15  0.80  0.03 -0.09  0.03 0.62 0.38
Q4_16   16  0.66  0.09 -0.22  0.20 0.52 0.48
Q4_17   17  0.77  0.06 -0.03 -0.14 0.50 0.50
Q4_18   18  1.02 -0.14 -0.12  0.02 0.73 0.27
Q4_19   19  0.79 -0.05  0.09 -0.04 0.62 0.38
Q5_1    20  0.37 -0.01  0.08  0.30 0.44 0.56
Q5_2    21  0.05  0.12  0.04  0.58 0.51 0.49
Q5_3    22  0.19  0.14 -0.14  0.58 0.53 0.47
Q5_4    23 -0.10 -0.14  0.08  0.88 0.64 0.36
Q5_5    24 -0.10 -0.22  0.08  0.88 0.59 0.41
Q5_6    25  0.09  0.02  0.01  0.73 0.65 0.35
Q5_7    26 -0.02  0.40  0.10  0.27 0.44 0.56
Q5_8    27 -0.05  0.13  0.08  0.67 0.60 0.40
Q5_9    28  0.20  0.29 -0.05  0.42 0.58 0.42
Q5_10   29  0.19  0.16  0.03  0.33 0.39 0.61
Q5_11   30  0.26  0.12  0.22  0.16 0.44 0.56
Q5_12   31  0.05  0.15  0.22  0.37 0.47 0.53
Q6_1    32 -0.05  0.90 -0.19 -0.04 0.55 0.45
Q6_2    33 -0.18  1.00 -0.15  0.03 0.66 0.34
Q6_3    34 -0.20  0.97 -0.15  0.05 0.62 0.38
Q6_4    35 -0.15  0.92 -0.18  0.02 0.54 0.46
Q6_5    36  0.07  0.37  0.18 -0.07 0.26 0.74
Q6_6    37  0.04  0.85 -0.04 -0.11 0.64 0.36
Q6_7    38  0.11  0.83  0.01 -0.17 0.68 0.32
Q6_8    39 -0.01  0.92  0.01 -0.20 0.68 0.32
Q6_9    40  0.13  0.22  0.47 -0.26 0.35 0.65
Q6_10   41  0.08  0.27  0.35 -0.02 0.37 0.63
Q6_11   42  0.01  0.36  0.38  0.09 0.55 0.45
Q7_1    43  0.15  0.32  0.25  0.16 0.59 0.41
Q7_2    44  0.06  0.15  0.46  0.14 0.51 0.49
Q7_3    45 -0.19 -0.10  0.85  0.12 0.58 0.42
Q7_4    46 -0.02  0.14  0.57  0.05 0.46 0.54
Q7_5    47  0.16  0.04  0.70 -0.08 0.63 0.37
Q7_6    48  0.08  0.11  0.64 -0.05 0.55 0.45
Q7_7    49 -0.02 -0.28  0.88  0.11 0.63 0.37
Q7_8    50  0.15 -0.04  0.65 -0.05 0.50 0.50
Q7_9    51  0.33  0.18  0.23  0.06 0.50 0.50
Q7_10   52  0.40  0.28  0.11  0.00 0.52 0.48
Q7_11   53  0.26 -0.02  0.52  0.00 0.50 0.50
Q7_12   54 -0.01 -0.05  0.72 -0.03 0.44 0.56
Q7_13   55 -0.15 -0.12  0.74 -0.14 0.27 0.73
Q7_14   56 -0.19 -0.22  0.76  0.18 0.44 0.56
Q7_15   57  0.31  0.20  0.19  0.04 0.44 0.56

                  PA1  PA3  PA2  PA4
SS loadings     10.68 6.66 7.10 5.32
Proportion Var   0.19 0.12 0.12 0.09
Cumulative Var   0.19 0.30 0.43 0.52
Cum. factor Var  0.36 0.58 0.82 1.00

 With factor correlations of 
     PA1  PA3  PA2  PA4
PA1 1.00 0.73 0.70 0.65
PA3 0.73 1.00 0.63 0.58
PA2 0.70 0.63 1.00 0.65
PA4 0.65 0.58 0.65 1.00

Mean item complexity =  1.5
Test of the hypothesis that 4 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1374  and the objective function was  10.73 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   PA1  PA3  PA2  PA4
Correlation of (regression) scores with factors   0.98 0.98 0.97 0.96
Multiple R square of scores with factors          0.97 0.95 0.94 0.92
Minimum correlation of possible factor scores     0.94 0.91 0.87 0.84

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA3    PA2    PA4   
Q4_1   0.806                     
Q4_2   0.794                     
Q4_3   0.769                     
Q4_4   0.645                     
Q4_5   0.602                     
Q4_6                             
Q4_7                             
Q4_8   0.885                     
Q4_9   0.783                     
Q4_10  0.560                     
Q4_11  0.727                     
Q4_12  0.522  0.371              
Q4_13  0.543                     
Q4_14  0.478                     
Q4_15  0.732                     
Q4_16  0.621                     
Q4_17  0.741                     
Q4_18  0.838                     
Q4_19  0.762                     
Q5_1   0.355                     
Q5_2                        0.597
Q5_3                        0.610
Q5_4                        0.970
Q5_5                        0.912
Q5_6                        0.664
Q5_7          0.376              
Q5_8                        0.710
Q5_9                        0.423
Q5_10                            
Q5_11                            
Q5_12                       0.351
Q6_1          0.763              
Q6_2          0.908              
Q6_3          0.897              
Q6_4          0.851              
Q6_5          0.382              
Q6_6          0.700              
Q6_7          0.725              
Q6_8          0.835              
Q6_9                 0.578 -0.312
Q6_10                0.317       
Q6_11         0.353  0.369       
Q7_1                             
Q7_2                 0.394       
Q7_3                 0.865       
Q7_4                 0.558       
Q7_5                 0.660       
Q7_6                 0.591       
Q7_7                 0.896       
Q7_8                 0.571       
Q7_9   0.323                     
Q7_10  0.383                     
Q7_11                0.434       
Q7_12                0.734       
Q7_13                0.732       
Q7_14                0.751       
Q7_15                            

                 PA1   PA3   PA2   PA4
SS loadings    9.520 6.311 6.238 4.572
Proportion Var 0.167 0.111 0.109 0.080
Cumulative Var 0.167 0.278 0.387 0.467

# rerun the above using the correlation matrix (pearson) to more easily get the standardized factor loadings.
fit <- psych::fa(r = corr.ppm, nfactors = 4, rotate = "Promax", fm = "pa", covar = T)
out.dat[,c(5:8)] <- fit$loadings
out.dat[,9] <- fit$communality
out.dat[,10] <- fit$uniquenesses

write.csv(out.dat, file="data/efa_results_2021_01_06.csv")

Five factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 5, rotate = "Promax", fm = "pa")
fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 5, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA1   PA3   PA2   PA4   PA5   h2   u2 com
Q4_1   1.02 -0.17 -0.13  0.01 -0.07 0.67 0.33 1.1
Q4_2   0.99 -0.16 -0.08  0.04 -0.01 0.72 0.28 1.1
Q4_3   1.01 -0.21 -0.05 -0.01 -0.08 0.67 0.33 1.1
Q4_4   0.94 -0.10  0.05 -0.03 -0.25 0.77 0.23 1.2
Q4_5   0.67  0.09 -0.10  0.14  0.02 0.59 0.41 1.2
Q4_6   0.30  0.10  0.11  0.29 -0.12 0.49 0.51 2.8
Q4_7   0.06  0.06  0.29  0.27 -0.16 0.36 0.64 2.7
Q4_8   0.97 -0.02 -0.13 -0.09  0.07 0.68 0.32 1.1
Q4_9   0.74 -0.09  0.14 -0.12  0.10 0.53 0.47 1.2
Q4_10  0.79 -0.04  0.11 -0.05 -0.13 0.63 0.37 1.1
Q4_11  0.72 -0.01  0.15 -0.04  0.10 0.67 0.33 1.1
Q4_12  0.39  0.34  0.09 -0.09  0.28 0.63 0.37 3.1
Q4_13  0.53  0.31 -0.10 -0.07  0.38 0.70 0.30 2.6
Q4_14  0.42  0.12  0.17  0.05  0.28 0.63 0.37 2.3
Q4_15  0.73  0.00 -0.03  0.10  0.18 0.69 0.31 1.2
Q4_16  0.63  0.11 -0.22  0.25  0.08 0.59 0.41 1.7
Q4_17  0.75  0.08 -0.01 -0.11  0.06 0.56 0.44 1.1
Q4_18  1.02 -0.13 -0.11  0.07  0.05 0.83 0.17 1.1
Q4_19  0.71 -0.03  0.15  0.00  0.13 0.68 0.32 1.2
Q5_1   0.32 -0.07  0.12  0.39  0.14 0.52 0.48 2.5
Q5_2  -0.01  0.09  0.02  0.66  0.09 0.56 0.44 1.1
Q5_3   0.09  0.05 -0.11  0.74  0.21 0.66 0.34 1.2
Q5_4  -0.08 -0.21  0.08  0.93 -0.08 0.67 0.33 1.2
Q5_5  -0.05 -0.27  0.06  0.89 -0.13 0.60 0.40 1.2
Q5_6   0.09 -0.04  0.00  0.80 -0.01 0.70 0.30 1.0
Q5_7  -0.09  0.40  0.13  0.32  0.07 0.50 0.50 2.3
Q5_8  -0.09  0.07  0.08  0.76  0.00 0.65 0.35 1.1
Q5_9   0.15  0.26 -0.05  0.53  0.05 0.66 0.34 1.7
Q5_10  0.18  0.18  0.03  0.36  0.01 0.45 0.55 2.1
Q5_11  0.20  0.08  0.27  0.25  0.05 0.51 0.49 3.1
Q5_12  0.01  0.16  0.20  0.43 -0.04 0.51 0.49 1.8
Q6_1  -0.09  0.95 -0.18 -0.01  0.14 0.67 0.33 1.1
Q6_2  -0.21  1.07 -0.18  0.06 -0.02 0.73 0.27 1.1
Q6_3  -0.18  1.05 -0.18  0.06 -0.03 0.72 0.28 1.1
Q6_4  -0.16  1.03 -0.23  0.01 -0.06 0.63 0.37 1.2
Q6_5   0.02  0.40  0.20 -0.03  0.08 0.33 0.67 1.6
Q6_6   0.04  0.96 -0.05 -0.12 -0.07 0.77 0.23 1.1
Q6_7   0.09  0.90  0.01 -0.17  0.03 0.78 0.22 1.1
Q6_8  -0.06  1.01  0.01 -0.19 -0.01 0.77 0.23 1.1
Q6_9  -0.02  0.16  0.64 -0.21  0.30 0.53 0.47 1.8
Q6_10  0.02  0.24  0.40  0.03  0.08 0.41 0.59 1.8
Q6_11 -0.04  0.38  0.39  0.12  0.03 0.59 0.41 2.2
Q7_1   0.13  0.38  0.25  0.17 -0.10 0.67 0.33 2.7
Q7_2   0.08  0.23  0.46  0.10 -0.14 0.58 0.42 1.9
Q7_3  -0.20 -0.08  0.88  0.11 -0.13 0.60 0.40 1.2
Q7_4   0.02  0.28  0.55 -0.03 -0.38 0.63 0.37 2.4
Q7_5   0.17  0.10  0.71 -0.11 -0.15 0.69 0.31 1.3
Q7_6   0.06  0.11  0.67 -0.04  0.00 0.59 0.41 1.1
Q7_7  -0.03 -0.36  0.98  0.14 -0.01 0.72 0.28 1.3
Q7_8   0.15 -0.01  0.68 -0.06 -0.12 0.55 0.45 1.2
Q7_9   0.34  0.26  0.22  0.06 -0.16 0.58 0.42 3.3
Q7_10  0.45  0.37  0.10 -0.01 -0.23 0.66 0.34 2.6
Q7_11  0.33  0.07  0.52 -0.08 -0.23 0.62 0.38 2.3
Q7_12 -0.07 -0.14  0.85 -0.02  0.11 0.53 0.47 1.1
Q7_13 -0.24 -0.26  0.90 -0.10  0.13 0.38 0.62 1.4
Q7_14 -0.18 -0.31  0.84  0.18 -0.07 0.48 0.52 1.5
Q7_15  0.33  0.29  0.17  0.03 -0.20 0.54 0.46 3.2

                        PA1  PA3  PA2  PA4  PA5
SS loadings           11.88 8.37 7.60 5.75 1.18
Proportion Var         0.21 0.15 0.13 0.10 0.02
Cumulative Var         0.21 0.36 0.49 0.59 0.61
Proportion Explained   0.34 0.24 0.22 0.17 0.03
Cumulative Proportion  0.34 0.58 0.80 0.97 1.00

 With factor correlations of 
     PA1  PA3  PA2  PA4  PA5
PA1 1.00 0.74 0.71 0.68 0.17
PA3 0.74 1.00 0.66 0.64 0.22
PA2 0.71 0.66 1.00 0.69 0.12
PA4 0.68 0.64 0.69 1.00 0.09
PA5 0.17 0.22 0.12 0.09 1.00

Mean item complexity =  1.6
Test of the hypothesis that 5 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1321  and the objective function was  40.74 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 0.99

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA3    PA2    PA4    PA5   
Q4_1   1.017                            
Q4_2   0.991                            
Q4_3   1.007                            
Q4_4   0.936                            
Q4_5   0.666                            
Q4_6                                    
Q4_7                                    
Q4_8   0.965                            
Q4_9   0.739                            
Q4_10  0.787                            
Q4_11  0.716                            
Q4_12  0.390  0.338                     
Q4_13  0.533  0.308                0.382
Q4_14  0.424                            
Q4_15  0.729                            
Q4_16  0.625                            
Q4_17  0.751                            
Q4_18  1.024                            
Q4_19  0.710                            
Q5_1   0.321                0.388       
Q5_2                        0.662       
Q5_3                        0.740       
Q5_4                        0.930       
Q5_5                        0.895       
Q5_6                        0.803       
Q5_7          0.404         0.317       
Q5_8                        0.764       
Q5_9                        0.528       
Q5_10                       0.358       
Q5_11                                   
Q5_12                       0.430       
Q6_1          0.950                     
Q6_2          1.066                     
Q6_3          1.049                     
Q6_4          1.033                     
Q6_5          0.396                     
Q6_6          0.964                     
Q6_7          0.898                     
Q6_8          1.015                     
Q6_9                 0.643              
Q6_10                0.396              
Q6_11         0.384  0.387              
Q7_1          0.382                     
Q7_2                 0.457              
Q7_3                 0.876              
Q7_4                 0.550        -0.384
Q7_5                 0.710              
Q7_6                 0.669              
Q7_7         -0.363  0.977              
Q7_8                 0.682              
Q7_9   0.335                            
Q7_10  0.445  0.374                     
Q7_11  0.332         0.519              
Q7_12                0.851              
Q7_13                0.897              
Q7_14        -0.306  0.836              
Q7_15  0.334                            

                  PA1   PA3   PA2   PA4   PA5
SS loadings    11.823 9.105 7.726 5.384 1.195
Proportion Var  0.207 0.160 0.136 0.094 0.021
Cumulative Var  0.207 0.367 0.503 0.597 0.618

fit <- psych::fa(r = cov.dat, nfactors = 5, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 5, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA3   PA4   PA2   PA5   h2   u2   H2   U2
Q4_1   0.82 -0.09  0.01 -0.04 -0.16 0.44 0.31 0.59 0.41
Q4_2   0.79 -0.11  0.01 -0.04 -0.07 0.43 0.24 0.64 0.36
Q4_3   0.79 -0.12 -0.01  0.02 -0.14 0.42 0.28 0.60 0.40
Q4_4   0.70 -0.02 -0.02  0.17 -0.24 0.45 0.22 0.67 0.33
Q4_5   0.58  0.05  0.09 -0.07 -0.01 0.41 0.37 0.52 0.48
Q4_6   0.29  0.14  0.25  0.15 -0.12 0.42 0.54 0.44 0.56
Q4_7   0.10  0.08  0.23  0.31 -0.13 0.30 0.58 0.35 0.65
Q4_8   0.86 -0.01 -0.09 -0.11 -0.02 0.52 0.34 0.61 0.39
Q4_9   0.75 -0.10 -0.14  0.07  0.09 0.48 0.53 0.47 0.53
Q4_10  0.60  0.00 -0.05  0.15 -0.15 0.34 0.28 0.55 0.45
Q4_11  0.69 -0.04 -0.06  0.07  0.12 0.55 0.36 0.60 0.40
Q4_12  0.46  0.23 -0.12 -0.05  0.30 0.57 0.54 0.51 0.49
Q4_13  0.47  0.14 -0.08 -0.22  0.27 0.39 0.38 0.51 0.49
Q4_14  0.41 -0.01  0.03  0.02  0.30 0.43 0.37 0.54 0.46
Q4_15  0.68 -0.05  0.06 -0.10  0.15 0.53 0.31 0.63 0.37
Q4_16  0.60  0.07  0.21 -0.18 -0.04 0.46 0.42 0.52 0.48
Q4_17  0.72  0.06 -0.14 -0.02  0.03 0.46 0.47 0.50 0.50
Q4_18  0.82 -0.10  0.02 -0.08 -0.02 0.50 0.18 0.73 0.27
Q4_19  0.72 -0.08 -0.02  0.05  0.12 0.58 0.36 0.62 0.38
Q5_1   0.28 -0.15  0.36  0.00  0.24 0.44 0.46 0.49 0.51
Q5_2   0.01  0.05  0.67  0.01  0.05 0.56 0.51 0.52 0.48
Q5_3   0.10 -0.07  0.76 -0.22  0.24 0.68 0.41 0.62 0.38
Q5_4  -0.08 -0.09  1.01  0.14 -0.27 0.78 0.45 0.63 0.37
Q5_5  -0.07 -0.13  0.94  0.14 -0.31 0.63 0.44 0.59 0.41
Q5_6   0.06 -0.02  0.72  0.01 -0.05 0.54 0.28 0.66 0.34
Q5_7  -0.05  0.27  0.30  0.06  0.15 0.40 0.49 0.45 0.55
Q5_8  -0.08  0.07  0.78  0.07  0.01 0.67 0.44 0.60 0.40
Q5_9   0.14  0.17  0.50 -0.07  0.13 0.60 0.39 0.60 0.40
Q5_10  0.14  0.10  0.31  0.02  0.03 0.28 0.43 0.39 0.61
Q5_11  0.21  0.03  0.20  0.15  0.18 0.41 0.50 0.45 0.55
Q5_12  0.04  0.12  0.38  0.19  0.02 0.42 0.48 0.47 0.53
Q6_1  -0.06  0.68 -0.02 -0.15  0.08 0.39 0.32 0.55 0.45
Q6_2  -0.13  0.93  0.02 -0.07 -0.12 0.58 0.25 0.69 0.31
Q6_3  -0.15  0.92  0.04 -0.08 -0.12 0.56 0.30 0.65 0.35
Q6_4  -0.10  0.92  0.00 -0.09 -0.18 0.51 0.35 0.59 0.41
Q6_5   0.02  0.25 -0.04  0.12  0.28 0.30 0.77 0.28 0.72
Q6_6   0.04  0.68 -0.09 -0.01  0.02 0.43 0.24 0.64 0.36
Q6_7   0.10  0.67 -0.15  0.01  0.10 0.52 0.24 0.68 0.32
Q6_8   0.00  0.78 -0.18  0.01  0.10 0.56 0.26 0.68 0.32
Q6_9   0.01 -0.05 -0.28  0.38  0.84 0.74 0.75 0.50 0.50
Q6_10  0.02  0.11  0.02  0.22  0.33 0.33 0.50 0.40 0.60
Q6_11 -0.02  0.26  0.11  0.29  0.23 0.52 0.42 0.55 0.45
Q7_1   0.13  0.26  0.16  0.20  0.08 0.48 0.34 0.59 0.41
Q7_2   0.07  0.16  0.11  0.37  0.01 0.38 0.35 0.52 0.48
Q7_3  -0.15 -0.01  0.09  0.80  0.02 0.61 0.42 0.59 0.41
Q7_4   0.06  0.30 -0.02  0.58 -0.18 0.52 0.44 0.54 0.46
Q7_5   0.18  0.08 -0.10  0.59  0.10 0.57 0.33 0.63 0.37
Q7_6   0.08  0.09 -0.05  0.51  0.17 0.46 0.38 0.55 0.45
Q7_7   0.00 -0.23  0.10  0.80  0.11 0.65 0.38 0.63 0.37
Q7_8   0.14 -0.01 -0.05  0.50  0.11 0.39 0.38 0.50 0.50
Q7_9   0.33  0.19  0.06  0.21  0.03 0.49 0.49 0.50 0.50
Q7_10  0.40  0.31 -0.02  0.12 -0.05 0.48 0.41 0.54 0.46
Q7_11  0.25  0.06 -0.03  0.42 -0.04 0.37 0.34 0.52 0.48
Q7_12 -0.04 -0.13 -0.01  0.60  0.33 0.47 0.58 0.45 0.55
Q7_13 -0.20 -0.24 -0.12  0.58  0.42 0.30 0.68 0.31 0.69
Q7_14 -0.16 -0.17  0.18  0.67  0.07 0.43 0.55 0.44 0.56
Q7_15  0.29  0.20  0.04  0.16  0.01 0.36 0.46 0.44 0.56

                       PA1  PA3  PA4  PA2  PA5
SS loadings           9.10 5.24 5.22 5.46 2.46
Proportion Var        0.18 0.10 0.10 0.11 0.05
Cumulative Var        0.18 0.28 0.39 0.49 0.54
Proportion Explained  0.33 0.19 0.19 0.20 0.09
Cumulative Proportion 0.33 0.52 0.71 0.91 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA3   PA4   PA2   PA5   h2   u2
Q4_1     1  0.95 -0.11  0.01 -0.04 -0.18 0.59 0.41
Q4_2     2  0.96 -0.13  0.01 -0.05 -0.08 0.64 0.36
Q4_3     3  0.94 -0.14 -0.01  0.03 -0.17 0.60 0.40
Q4_4     4  0.86 -0.02 -0.02  0.20 -0.29 0.67 0.33
Q4_5     5  0.66  0.06  0.10 -0.08 -0.01 0.52 0.48
Q4_6     6  0.30  0.14  0.26  0.16 -0.12 0.44 0.56
Q4_7     7  0.11  0.09  0.25  0.33 -0.14 0.35 0.65
Q4_8     8  0.93 -0.01 -0.10 -0.12 -0.02 0.61 0.39
Q4_9     9  0.75 -0.10 -0.14  0.07  0.09 0.47 0.53
Q4_10   10  0.75  0.00 -0.06  0.19 -0.19 0.55 0.45
Q4_11   11  0.73 -0.04 -0.06  0.07  0.12 0.60 0.40
Q4_12   12  0.43  0.22 -0.12 -0.05  0.28 0.51 0.49
Q4_13   13  0.54  0.15 -0.09 -0.25  0.31 0.51 0.49
Q4_14   14  0.46 -0.02  0.03  0.02  0.33 0.54 0.46
Q4_15   15  0.74 -0.06  0.07 -0.11  0.16 0.63 0.37
Q4_16   16  0.63  0.08  0.22 -0.19 -0.05 0.52 0.48
Q4_17   17  0.75  0.06 -0.15 -0.02  0.03 0.50 0.50
Q4_18   18  0.99 -0.12  0.03 -0.10 -0.03 0.73 0.27
Q4_19   19  0.74 -0.09 -0.02  0.05  0.13 0.62 0.38
Q5_1    20  0.30 -0.16  0.38  0.00  0.26 0.49 0.51
Q5_2    21  0.01  0.05  0.65  0.01  0.04 0.52 0.48
Q5_3    22  0.10 -0.06  0.72 -0.21  0.23 0.62 0.38
Q5_4    23 -0.07 -0.08  0.91  0.13 -0.24 0.63 0.37
Q5_5    24 -0.07 -0.13  0.91  0.13 -0.30 0.59 0.41
Q5_6    25  0.07 -0.02  0.80  0.02 -0.06 0.66 0.34
Q5_7    26 -0.05  0.29  0.32  0.06  0.16 0.45 0.55
Q5_8    27 -0.07  0.06  0.74  0.06  0.01 0.60 0.40
Q5_9    28  0.14  0.17  0.50 -0.07  0.13 0.60 0.40
Q5_10   29  0.16  0.11  0.37  0.02  0.04 0.39 0.61
Q5_11   30  0.22  0.03  0.21  0.16  0.19 0.45 0.55
Q5_12   31  0.04  0.12  0.40  0.20  0.03 0.47 0.53
Q6_1    32 -0.07  0.81 -0.02 -0.18  0.09 0.55 0.45
Q6_2    33 -0.15  1.03  0.02 -0.08 -0.13 0.69 0.31
Q6_3    34 -0.16  1.00  0.04 -0.08 -0.13 0.65 0.35
Q6_4    35 -0.11  0.99  0.00 -0.10 -0.20 0.59 0.41
Q6_5    36  0.02  0.25 -0.04  0.11  0.27 0.28 0.72
Q6_6    37  0.05  0.83 -0.11 -0.02  0.02 0.64 0.36
Q6_7    38  0.11  0.77 -0.17  0.01  0.11 0.68 0.32
Q6_8    39  0.00  0.86 -0.20  0.01  0.11 0.68 0.32
Q6_9    40  0.01 -0.04 -0.23  0.31  0.68 0.50 0.50
Q6_10   41  0.02  0.12  0.02  0.24  0.36 0.40 0.60
Q6_11   42 -0.02  0.27  0.12  0.30  0.24 0.55 0.45
Q7_1    43  0.14  0.29  0.18  0.22  0.09 0.59 0.41
Q7_2    44  0.09  0.19  0.13  0.43  0.01 0.52 0.48
Q7_3    45 -0.15 -0.01  0.09  0.79  0.02 0.59 0.41
Q7_4    46  0.06  0.31 -0.02  0.60 -0.18 0.54 0.46
Q7_5    47  0.18  0.08 -0.10  0.63  0.10 0.63 0.37
Q7_6    48  0.08  0.09 -0.06  0.55  0.18 0.55 0.45
Q7_7    49  0.00 -0.22  0.10  0.78  0.11 0.63 0.37
Q7_8    50  0.16 -0.01 -0.06  0.57  0.13 0.50 0.50
Q7_9    51  0.33  0.19  0.06  0.22  0.03 0.50 0.50
Q7_10   52  0.42  0.33 -0.02  0.13 -0.05 0.54 0.46
Q7_11   53  0.30  0.07 -0.03  0.50 -0.04 0.52 0.48
Q7_12   54 -0.04 -0.13 -0.01  0.58  0.33 0.45 0.55
Q7_13   55 -0.20 -0.24 -0.12  0.58  0.43 0.31 0.69
Q7_14   56 -0.16 -0.18  0.18  0.68  0.07 0.44 0.56
Q7_15   57  0.32  0.22  0.04  0.18  0.01 0.44 0.56

                  PA1  PA3  PA4  PA2  PA5
SS loadings     10.22 5.88 5.86 6.14 2.76
Proportion Var   0.18 0.10 0.10 0.11 0.05
Cumulative Var   0.18 0.28 0.39 0.49 0.54
Cum. factor Var  0.33 0.52 0.71 0.91 1.00

 With factor correlations of 
     PA1  PA3  PA4  PA2  PA5
PA1 1.00 0.70 0.69 0.61 0.62
PA3 0.70 1.00 0.62 0.51 0.65
PA4 0.69 0.62 1.00 0.63 0.58
PA2 0.61 0.51 0.63 1.00 0.42
PA5 0.62 0.65 0.58 0.42 1.00

Mean item complexity =  1.7
Test of the hypothesis that 5 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1321  and the objective function was  9.85 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   PA1  PA3  PA4  PA2  PA5
Correlation of (regression) scores with factors   0.98 0.98 0.97 0.96 0.92
Multiple R square of scores with factors          0.97 0.95 0.93 0.92 0.84
Minimum correlation of possible factor scores     0.94 0.90 0.87 0.84 0.68

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA3    PA4    PA2    PA5   
Q4_1   0.820                            
Q4_2   0.785                            
Q4_3   0.785                            
Q4_4   0.701                            
Q4_5   0.583                            
Q4_6                                    
Q4_7                        0.311       
Q4_8   0.865                            
Q4_9   0.754                            
Q4_10  0.595                            
Q4_11  0.692                            
Q4_12  0.456                            
Q4_13  0.470                            
Q4_14  0.409                            
Q4_15  0.676                            
Q4_16  0.597                            
Q4_17  0.723                            
Q4_18  0.815                            
Q4_19  0.721                            
Q5_1                 0.360              
Q5_2                 0.672              
Q5_3                 0.757              
Q5_4                 1.009              
Q5_5                 0.941        -0.310
Q5_6                 0.722              
Q5_7                 0.302              
Q5_8                 0.783              
Q5_9                 0.496              
Q5_10                0.312              
Q5_11                                   
Q5_12                0.383              
Q6_1          0.682                     
Q6_2          0.935                     
Q6_3          0.924                     
Q6_4          0.917                     
Q6_5                                    
Q6_6          0.679                     
Q6_7          0.671                     
Q6_8          0.777                     
Q6_9                        0.383  0.836
Q6_10                              0.328
Q6_11                                   
Q7_1                                    
Q7_2                        0.368       
Q7_3                        0.802       
Q7_4                        0.584       
Q7_5                        0.595       
Q7_6                        0.509       
Q7_7                        0.796       
Q7_8                        0.504       
Q7_9   0.326                            
Q7_10  0.401  0.310                     
Q7_11                       0.418       
Q7_12                       0.596  0.333
Q7_13                       0.578  0.422
Q7_14                       0.670       
Q7_15                                   

                 PA1   PA3   PA4   PA2   PA5
SS loadings    8.951 5.582 5.349 4.857 2.260
Proportion Var 0.157 0.098 0.094 0.085 0.040
Cumulative Var 0.157 0.255 0.349 0.434 0.474

Six factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 6,
          rotate = "Promax", fm = "pa")
fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 6, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA1   PA6   PA2   PA4   PA5   PA3   h2   u2 com
Q4_1   0.85 -0.12 -0.10  0.01  0.18 -0.07 0.67 0.33 1.2
Q4_2   0.82 -0.14 -0.08  0.03  0.15  0.05 0.72 0.28 1.2
Q4_3   0.86 -0.13 -0.02  0.00  0.14 -0.08 0.68 0.32 1.1
Q4_4   0.83  0.00  0.11 -0.02  0.21 -0.30 0.78 0.22 1.4
Q4_5   0.52  0.03 -0.12  0.13  0.18  0.10 0.59 0.41 1.6
Q4_6   0.30  0.15  0.16  0.29  0.06 -0.15 0.50 0.50 3.7
Q4_7   0.15  0.20  0.38  0.28 -0.09 -0.23 0.42 0.58 3.8
Q4_8   0.86  0.04 -0.05 -0.08 -0.06  0.11 0.69 0.31 1.1
Q4_9   0.65 -0.04  0.14 -0.11 -0.06  0.18 0.53 0.47 1.4
Q4_10  0.77  0.11  0.21 -0.04 -0.03 -0.18 0.68 0.32 1.3
Q4_11  0.63  0.02  0.14 -0.03 -0.02  0.20 0.67 0.33 1.3
Q4_12  0.39  0.33  0.13 -0.08 -0.28  0.43 0.65 0.35 4.0
Q4_13  0.42  0.18 -0.14 -0.07 -0.13  0.60 0.71 0.29 2.3
Q4_14  0.37  0.09  0.13  0.05 -0.16  0.45 0.62 0.38 2.5
Q4_15  0.62  0.00 -0.02  0.10 -0.06  0.29 0.69 0.31 1.5
Q4_16  0.57  0.15 -0.13  0.25 -0.09  0.09 0.60 0.40 1.8
Q4_17  0.67  0.10  0.03 -0.10 -0.02  0.12 0.56 0.44 1.2
Q4_18  0.87 -0.09 -0.08  0.07  0.04  0.11 0.83 0.17 1.1
Q4_19  0.63  0.01  0.15  0.00 -0.08  0.24 0.69 0.31 1.4
Q5_1   0.16 -0.21 -0.04  0.37  0.22  0.33 0.57 0.43 3.8
Q5_2  -0.01  0.07  0.03  0.64 -0.05  0.15 0.56 0.44 1.2
Q5_3  -0.02 -0.08 -0.19  0.72  0.05  0.36 0.69 0.31 1.7
Q5_4  -0.01 -0.07  0.18  0.91 -0.13 -0.16 0.69 0.31 1.2
Q5_5   0.01 -0.12  0.15  0.87 -0.08 -0.22 0.61 0.39 1.3
Q5_6   0.07 -0.02  0.02  0.77  0.02  0.01 0.70 0.30 1.0
Q5_7  -0.04  0.36  0.14  0.31 -0.07  0.16 0.50 0.50 2.9
Q5_8  -0.09  0.04  0.07  0.73  0.06  0.05 0.65 0.35 1.1
Q5_9   0.05  0.11 -0.13  0.50  0.23  0.17 0.68 0.32 1.9
Q5_10  0.12  0.11 -0.01  0.34  0.13  0.10 0.45 0.55 2.0
Q5_11  0.08 -0.05  0.10  0.24  0.28  0.22 0.53 0.47 3.5
Q5_12 -0.03  0.08  0.12  0.41  0.20  0.04 0.51 0.49 1.8
Q6_1  -0.08  0.74 -0.17 -0.01  0.05  0.24 0.67 0.33 1.4
Q6_2  -0.10  0.96 -0.06  0.07 -0.03 -0.04 0.76 0.24 1.0
Q6_3  -0.04  1.00 -0.02  0.08 -0.13 -0.07 0.79 0.21 1.1
Q6_4  -0.04  0.97 -0.07  0.02 -0.08 -0.11 0.68 0.32 1.1
Q6_5  -0.06  0.20  0.05 -0.04  0.26  0.26 0.35 0.65 3.1
Q6_6   0.02  0.73 -0.08 -0.11  0.29  0.04 0.76 0.24 1.4
Q6_7   0.11  0.75  0.03 -0.16  0.06  0.13 0.78 0.22 1.2
Q6_8  -0.04  0.80 -0.01 -0.18  0.18  0.11 0.76 0.24 1.2
Q6_9  -0.05  0.04  0.43 -0.20 -0.02  0.58 0.53 0.47 2.2
Q6_10 -0.06  0.09  0.22  0.02  0.23  0.27 0.42 0.58 3.2
Q6_11 -0.02  0.30  0.31  0.12  0.08  0.16 0.59 0.41 3.0
Q7_1  -0.04  0.12  0.01  0.15  0.63  0.08 0.73 0.27 1.2
Q7_2   0.04  0.15  0.33  0.09  0.31 -0.04 0.57 0.43 2.6
Q7_3  -0.05  0.11  0.89  0.12 -0.18 -0.12 0.68 0.32 1.2
Q7_4  -0.02  0.19  0.40 -0.03  0.54 -0.33 0.62 0.38 2.9
Q7_5   0.10  0.02  0.51 -0.11  0.38  0.01 0.69 0.31 2.1
Q7_6   0.09  0.13  0.57 -0.03  0.01  0.13 0.60 0.40 1.3
Q7_7   0.08 -0.16  0.93  0.14 -0.21  0.06 0.78 0.22 1.2
Q7_8   0.08 -0.08  0.48 -0.06  0.33  0.04 0.55 0.45 1.9
Q7_9   0.09 -0.04 -0.07  0.02  0.82  0.02 0.70 0.30 1.0
Q7_10  0.19  0.08 -0.16 -0.04  0.88 -0.10 0.77 0.23 1.2
Q7_11  0.18 -0.06  0.29 -0.09  0.59 -0.10 0.64 0.36 1.9
Q7_12 -0.10 -0.18  0.61 -0.02  0.11  0.32 0.53 0.47 1.9
Q7_13 -0.19 -0.21  0.71 -0.10 -0.09  0.29 0.37 0.63 1.8
Q7_14 -0.08 -0.14  0.78  0.18 -0.12 -0.05 0.50 0.50 1.3
Q7_15  0.10  0.01 -0.09  0.00  0.82 -0.06 0.64 0.36 1.1

                       PA1  PA6  PA2  PA4  PA5  PA3
SS loadings           9.63 6.37 5.74 5.54 5.12 3.52
Proportion Var        0.17 0.11 0.10 0.10 0.09 0.06
Cumulative Var        0.17 0.28 0.38 0.48 0.57 0.63
Proportion Explained  0.27 0.18 0.16 0.15 0.14 0.10
Cumulative Proportion 0.27 0.45 0.61 0.76 0.90 1.00

 With factor correlations of 
     PA1  PA6  PA2  PA4  PA5  PA3
PA1 1.00 0.60 0.56 0.63 0.69 0.59
PA6 0.60 1.00 0.46 0.55 0.66 0.61
PA2 0.56 0.46 1.00 0.60 0.68 0.46
PA4 0.63 0.55 0.60 1.00 0.66 0.52
PA5 0.69 0.66 0.68 0.66 1.00 0.66
PA3 0.59 0.61 0.46 0.52 0.66 1.00

Mean item complexity =  1.8
Test of the hypothesis that 6 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1269  and the objective function was  39.16 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 0.99

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA6    PA2    PA4    PA5    PA3   
Q4_1   0.849                                   
Q4_2   0.815                                   
Q4_3   0.859                                   
Q4_4   0.835                                   
Q4_5   0.523                                   
Q4_6                                           
Q4_7                 0.377                     
Q4_8   0.857                                   
Q4_9   0.653                                   
Q4_10  0.767                                   
Q4_11  0.626                                   
Q4_12  0.392  0.325                       0.428
Q4_13  0.420                              0.598
Q4_14  0.369                              0.446
Q4_15  0.618                                   
Q4_16  0.567                                   
Q4_17  0.666                                   
Q4_18  0.869                                   
Q4_19  0.628                                   
Q5_1                        0.370         0.334
Q5_2                        0.637              
Q5_3                        0.715         0.363
Q5_4                        0.910              
Q5_5                        0.873              
Q5_6                        0.773              
Q5_7          0.355         0.311              
Q5_8                        0.734              
Q5_9                        0.505              
Q5_10                       0.344              
Q5_11                                          
Q5_12                       0.410              
Q6_1          0.738                            
Q6_2          0.959                            
Q6_3          1.005                            
Q6_4          0.974                            
Q6_5                                           
Q6_6          0.734                            
Q6_7          0.749                            
Q6_8          0.799                            
Q6_9                 0.432                0.582
Q6_10                                          
Q6_11         0.304  0.308                     
Q7_1                               0.629       
Q7_2                 0.331         0.307       
Q7_3                 0.891                     
Q7_4                 0.399         0.544 -0.326
Q7_5                 0.507         0.378       
Q7_6                 0.573                     
Q7_7                 0.928                     
Q7_8                 0.484         0.328       
Q7_9                               0.821       
Q7_10                              0.880       
Q7_11                              0.589       
Q7_12                0.610                0.323
Q7_13                0.707                     
Q7_14                0.777                     
Q7_15                              0.815       

                 PA1   PA6   PA2   PA4   PA5   PA3
SS loadings    8.393 6.097 5.277 5.044 4.466 2.648
Proportion Var 0.147 0.107 0.093 0.088 0.078 0.046
Cumulative Var 0.147 0.254 0.347 0.435 0.514 0.560

fit <- psych::fa(r = cov.dat, nfactors = 6, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 6, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA4   PA3   PA5   PA2   PA6   h2   u2   H2   U2
Q4_1   0.68  0.01 -0.10  0.21 -0.06 -0.17 0.44 0.31 0.59 0.41
Q4_2   0.68  0.01 -0.10  0.12 -0.05 -0.07 0.43 0.24 0.64 0.36
Q4_3   0.67  0.00 -0.10  0.14  0.01 -0.15 0.41 0.28 0.60 0.40
Q4_4   0.60  0.00 -0.01  0.19  0.12 -0.25 0.44 0.22 0.67 0.33
Q4_5   0.48  0.08  0.02  0.17 -0.09 -0.01 0.41 0.37 0.52 0.48
Q4_6   0.26  0.26  0.14  0.10  0.13 -0.12 0.42 0.54 0.44 0.56
Q4_7   0.15  0.26  0.14 -0.09  0.33 -0.13 0.32 0.56 0.37 0.63
Q4_8   0.81 -0.07  0.03 -0.04 -0.05 -0.01 0.53 0.33 0.62 0.38
Q4_9   0.73 -0.11 -0.03 -0.08  0.12  0.10 0.50 0.52 0.49 0.51
Q4_10  0.56 -0.02  0.05  0.01  0.17 -0.15 0.35 0.27 0.56 0.44
Q4_11  0.64 -0.04 -0.01  0.00  0.09  0.14 0.56 0.36 0.61 0.39
Q4_12  0.52 -0.09  0.29 -0.28  0.07  0.36 0.61 0.49 0.55 0.45
Q4_13  0.48 -0.06  0.16 -0.16 -0.12  0.31 0.40 0.37 0.52 0.48
Q4_14  0.42  0.04  0.03 -0.12  0.07  0.33 0.44 0.36 0.55 0.45
Q4_15  0.63  0.07 -0.02 -0.04 -0.05  0.17 0.53 0.31 0.63 0.37
Q4_16  0.56  0.22  0.10 -0.05 -0.10 -0.03 0.47 0.42 0.53 0.47
Q4_17  0.68 -0.12  0.09 -0.01  0.02  0.04 0.47 0.46 0.51 0.49
Q4_18  0.73  0.03 -0.07  0.04 -0.05 -0.02 0.50 0.18 0.73 0.27
Q4_19  0.69  0.00 -0.02 -0.07  0.10  0.14 0.60 0.34 0.63 0.37
Q5_1   0.18  0.32 -0.21  0.21 -0.07  0.26 0.46 0.45 0.51 0.49
Q5_2   0.03  0.66  0.06 -0.04  0.04  0.06 0.56 0.51 0.52 0.48
Q5_3   0.06  0.72 -0.09  0.04 -0.21  0.26 0.68 0.41 0.62 0.38
Q5_4  -0.02  1.04  0.00 -0.17  0.20 -0.27 0.80 0.42 0.65 0.35
Q5_5  -0.03  0.96 -0.06 -0.11  0.18 -0.32 0.64 0.43 0.60 0.40
Q5_6   0.05  0.71 -0.01  0.03  0.02 -0.05 0.54 0.28 0.65 0.35
Q5_7  -0.01  0.31  0.25 -0.05  0.08  0.18 0.40 0.48 0.45 0.55
Q5_8  -0.09  0.76  0.04  0.09  0.04  0.02 0.67 0.44 0.60 0.40
Q5_9   0.05  0.46  0.06  0.28 -0.15  0.14 0.62 0.37 0.62 0.38
Q5_10  0.10  0.30  0.06  0.11 -0.01  0.04 0.28 0.42 0.39 0.61
Q5_11  0.11  0.16 -0.05  0.30  0.03  0.19 0.43 0.48 0.47 0.53
Q5_12  0.00  0.36  0.06  0.20  0.11  0.03 0.43 0.48 0.47 0.53
Q6_1  -0.02 -0.01  0.60  0.00 -0.11  0.10 0.39 0.32 0.55 0.45
Q6_2  -0.06  0.05  0.86 -0.01 -0.01 -0.11 0.59 0.24 0.71 0.29
Q6_3  -0.05  0.08  0.88 -0.11  0.02 -0.11 0.59 0.26 0.70 0.30
Q6_4  -0.02  0.03  0.86 -0.05 -0.01 -0.18 0.54 0.32 0.62 0.38
Q6_5  -0.03 -0.06  0.15  0.24  0.02  0.30 0.31 0.76 0.29 0.71
Q6_6   0.02 -0.09  0.56  0.19 -0.04  0.02 0.43 0.24 0.64 0.36
Q6_7   0.11 -0.14  0.59  0.07  0.02  0.12 0.52 0.24 0.68 0.32
Q6_8  -0.01 -0.18  0.64  0.18 -0.02  0.12 0.55 0.26 0.68 0.32
Q6_9   0.06 -0.28 -0.04 -0.08  0.33  0.90 0.74 0.75 0.49 0.51
Q6_10 -0.03  0.00  0.03  0.21  0.12  0.35 0.34 0.50 0.41 0.59
Q6_11 -0.01  0.11  0.22  0.08  0.24  0.26 0.52 0.42 0.55 0.45
Q7_1  -0.04  0.10  0.08  0.59 -0.01  0.06 0.54 0.28 0.66 0.34
Q7_2   0.01  0.10  0.09  0.28  0.24  0.01 0.38 0.35 0.52 0.48
Q7_3  -0.03  0.14  0.10 -0.15  0.79  0.04 0.66 0.36 0.65 0.35
Q7_4  -0.07 -0.05  0.16  0.57  0.36 -0.21 0.55 0.41 0.57 0.43
Q7_5   0.08 -0.12  0.00  0.41  0.40  0.10 0.58 0.32 0.64 0.36
Q7_6   0.10 -0.03  0.10  0.04  0.45  0.19 0.47 0.38 0.55 0.45
Q7_7   0.10  0.15 -0.09 -0.19  0.79  0.14 0.70 0.33 0.68 0.32
Q7_8   0.08 -0.06 -0.06  0.28  0.36  0.11 0.39 0.38 0.50 0.50
Q7_9   0.06 -0.03 -0.05  0.86 -0.08 -0.02 0.63 0.35 0.64 0.36
Q7_10  0.14 -0.11  0.07  0.85 -0.14 -0.11 0.61 0.28 0.68 0.32
Q7_11  0.11 -0.07 -0.05  0.50  0.22 -0.06 0.39 0.31 0.56 0.44
Q7_12 -0.05 -0.01 -0.13  0.12  0.47  0.36 0.47 0.58 0.45 0.55
Q7_13 -0.12 -0.10 -0.16 -0.12  0.53  0.46 0.31 0.67 0.31 0.69
Q7_14 -0.07  0.21 -0.07 -0.13  0.64  0.09 0.45 0.53 0.46 0.54
Q7_15  0.06 -0.05 -0.01  0.76 -0.09 -0.04 0.47 0.35 0.57 0.43

                       PA1  PA4  PA3  PA5  PA2  PA6
SS loadings           7.76 5.12 4.31 4.38 4.13 2.74
Proportion Var        0.15 0.10 0.08 0.09 0.08 0.05
Cumulative Var        0.15 0.25 0.34 0.42 0.51 0.56
Proportion Explained  0.27 0.18 0.15 0.15 0.15 0.10
Cumulative Proportion 0.27 0.45 0.60 0.76 0.90 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA4   PA3   PA5   PA2   PA6   h2   u2
Q4_1     1  0.79  0.01 -0.12  0.24 -0.07 -0.20 0.59 0.41
Q4_2     2  0.83  0.01 -0.12  0.14 -0.06 -0.09 0.64 0.36
Q4_3     3  0.81  0.00 -0.12  0.17  0.01 -0.19 0.60 0.40
Q4_4     4  0.73 -0.01 -0.02  0.23  0.15 -0.31 0.67 0.33
Q4_5     5  0.55  0.09  0.02  0.19 -0.11 -0.01 0.52 0.48
Q4_6     6  0.27  0.27  0.14  0.10  0.14 -0.12 0.44 0.56
Q4_7     7  0.16  0.28  0.15 -0.09  0.35 -0.13 0.37 0.63
Q4_8     8  0.87 -0.08  0.04 -0.04 -0.05 -0.01 0.62 0.38
Q4_9     9  0.72 -0.11 -0.03 -0.08  0.12  0.10 0.49 0.51
Q4_10   10  0.71 -0.02  0.06  0.01  0.22 -0.19 0.56 0.44
Q4_11   11  0.67 -0.04 -0.01 -0.01  0.09  0.14 0.61 0.39
Q4_12   12  0.50 -0.08  0.28 -0.27  0.06  0.34 0.55 0.45
Q4_13   13  0.54 -0.07  0.18 -0.18 -0.14  0.35 0.52 0.48
Q4_14   14  0.46  0.05  0.03 -0.13  0.07  0.37 0.55 0.45
Q4_15   15  0.68  0.08 -0.02 -0.05 -0.06  0.18 0.63 0.37
Q4_16   16  0.60  0.24  0.11 -0.06 -0.11 -0.04 0.53 0.47
Q4_17   17  0.70 -0.12  0.09 -0.01  0.02  0.05 0.51 0.49
Q4_18   18  0.88  0.04 -0.08  0.05 -0.07 -0.02 0.73 0.27
Q4_19   19  0.71  0.00 -0.02 -0.07  0.10  0.15 0.63 0.37
Q5_1    20  0.19  0.34 -0.22  0.22 -0.08  0.27 0.51 0.49
Q5_2    21  0.03  0.64  0.06 -0.04  0.04  0.06 0.52 0.48
Q5_3    22  0.06  0.69 -0.09  0.04 -0.20  0.24 0.62 0.38
Q5_4    23 -0.02  0.94  0.00 -0.15  0.18 -0.24 0.65 0.35
Q5_5    24 -0.03  0.92 -0.06 -0.11  0.17 -0.31 0.60 0.40
Q5_6    25  0.05  0.78 -0.01  0.03  0.02 -0.05 0.65 0.35
Q5_7    26 -0.01  0.33  0.27 -0.05  0.08  0.20 0.45 0.55
Q5_8    27 -0.09  0.72  0.04  0.08  0.03  0.02 0.60 0.40
Q5_9    28  0.05  0.46  0.06  0.28 -0.15  0.14 0.62 0.38
Q5_10   29  0.12  0.36  0.07  0.13 -0.01  0.05 0.39 0.61
Q5_11   30  0.11  0.17 -0.06  0.32  0.03  0.20 0.47 0.53
Q5_12   31  0.00  0.38  0.07  0.21  0.12  0.03 0.47 0.53
Q6_1    32 -0.02 -0.01  0.71  0.00 -0.13  0.11 0.55 0.45
Q6_2    33 -0.07  0.05  0.94 -0.01 -0.01 -0.12 0.71 0.29
Q6_3    34 -0.05  0.08  0.95 -0.12  0.02 -0.12 0.70 0.30
Q6_4    35 -0.02  0.03  0.93 -0.05 -0.01 -0.19 0.62 0.38
Q6_5    36 -0.03 -0.06  0.14  0.24  0.02  0.29 0.29 0.71
Q6_6    37  0.03 -0.11  0.68  0.23 -0.05  0.03 0.64 0.36
Q6_7    38  0.13 -0.16  0.67  0.08  0.02  0.13 0.68 0.32
Q6_8    39 -0.01 -0.20  0.71  0.20 -0.03  0.13 0.68 0.32
Q6_9    40  0.05 -0.23 -0.03 -0.06  0.27  0.74 0.49 0.51
Q6_10   41 -0.03  0.00  0.03  0.23  0.13  0.38 0.41 0.59
Q6_11   42 -0.01  0.12  0.22  0.09  0.25  0.27 0.55 0.45
Q7_1    43 -0.04  0.11  0.09  0.65 -0.01  0.07 0.66 0.34
Q7_2    44  0.02  0.11  0.11  0.33  0.29  0.01 0.52 0.48
Q7_3    45 -0.03  0.14  0.10 -0.15  0.78  0.04 0.65 0.35
Q7_4    46 -0.07 -0.05  0.16  0.58  0.36 -0.21 0.57 0.43
Q7_5    47  0.09 -0.12  0.00  0.43  0.43  0.10 0.64 0.36
Q7_6    48  0.11 -0.04  0.11  0.04  0.49  0.21 0.55 0.45
Q7_7    49  0.10  0.15 -0.09 -0.19  0.78  0.14 0.68 0.32
Q7_8    50  0.09 -0.07 -0.07  0.32  0.41  0.13 0.50 0.50
Q7_9    51  0.06 -0.03 -0.05  0.87 -0.08 -0.02 0.64 0.36
Q7_10   52  0.15 -0.11  0.08  0.90 -0.15 -0.12 0.68 0.32
Q7_11   53  0.13 -0.08 -0.06  0.60  0.26 -0.07 0.56 0.44
Q7_12   54 -0.04 -0.01 -0.13  0.12  0.46  0.35 0.45 0.55
Q7_13   55 -0.12 -0.11 -0.16 -0.12  0.53  0.47 0.31 0.69
Q7_14   56 -0.07  0.21 -0.07 -0.13  0.65  0.10 0.46 0.54
Q7_15   57  0.07 -0.05 -0.02  0.84 -0.10 -0.04 0.57 0.43

                 PA1  PA4  PA3  PA5  PA2  PA6
SS loadings     8.71 5.75 4.84 4.92 4.64 3.08
Proportion Var  0.15 0.10 0.08 0.09 0.08 0.05
Cumulative Var  0.15 0.25 0.34 0.42 0.51 0.56
Cum. factor Var 0.27 0.45 0.60 0.76 0.90 1.00

 With factor correlations of 
     PA1  PA4  PA3  PA5  PA2  PA6
PA1 1.00 0.65 0.59 0.73 0.45 0.62
PA4 0.65 1.00 0.55 0.72 0.51 0.61
PA3 0.59 0.55 1.00 0.65 0.31 0.64
PA5 0.73 0.72 0.65 1.00 0.60 0.69
PA2 0.45 0.51 0.31 0.60 1.00 0.35
PA6 0.62 0.61 0.64 0.69 0.35 1.00

Mean item complexity =  1.7
Test of the hypothesis that 6 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1269  and the objective function was  8.78 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   PA1  PA4  PA3  PA5  PA2  PA6
Correlation of (regression) scores with factors   0.98 0.97 0.97 0.97 0.95 0.93
Multiple R square of scores with factors          0.96 0.93 0.94 0.94 0.90 0.86
Minimum correlation of possible factor scores     0.92 0.86 0.88 0.87 0.80 0.72

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA4    PA3    PA5    PA2    PA6   
Q4_1   0.684                                   
Q4_2   0.678                                   
Q4_3   0.674                                   
Q4_4   0.599                                   
Q4_5   0.484                                   
Q4_6                                           
Q4_7                               0.331       
Q4_8   0.805                                   
Q4_9   0.726                                   
Q4_10  0.561                                   
Q4_11  0.644                                   
Q4_12  0.523                              0.358
Q4_13  0.477                              0.308
Q4_14  0.416                              0.331
Q4_15  0.628                                   
Q4_16  0.562                                   
Q4_17  0.677                                   
Q4_18  0.727                                   
Q4_19  0.690                                   
Q5_1          0.321                            
Q5_2          0.664                            
Q5_3          0.719                            
Q5_4          1.035                            
Q5_5          0.956                      -0.317
Q5_6          0.708                            
Q5_7          0.309                            
Q5_8          0.760                            
Q5_9          0.456                            
Q5_10                                          
Q5_11                       0.305              
Q5_12         0.364                            
Q6_1                 0.601                     
Q6_2                 0.856                     
Q6_3                 0.883                     
Q6_4                 0.859                     
Q6_5                                           
Q6_6                 0.557                     
Q6_7                 0.587                     
Q6_8                 0.643                     
Q6_9                               0.334  0.899
Q6_10                                     0.347
Q6_11                                          
Q7_1                        0.588              
Q7_2                                           
Q7_3                               0.789       
Q7_4                        0.572  0.357       
Q7_5                        0.405  0.403       
Q7_6                               0.450       
Q7_7                               0.789       
Q7_8                               0.357       
Q7_9                        0.860              
Q7_10                       0.848              
Q7_11                       0.504              
Q7_12                              0.472  0.357
Q7_13                              0.528  0.461
Q7_14                              0.639       
Q7_15                       0.757              

                 PA1   PA4   PA3   PA5   PA2   PA6
SS loadings    7.021 5.244 4.229 4.209 3.544 2.665
Proportion Var 0.123 0.092 0.074 0.074 0.062 0.047
Cumulative Var 0.123 0.215 0.289 0.363 0.425 0.472

Seven factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 7, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 7, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA3   PA4   PA2   PA5   PA6   PA1   PA7   h2   u2 com
Q4_1   0.88 -0.01  0.01  0.22 -0.16 -0.18  0.08 0.74 0.26 1.3
Q4_2   0.77  0.03 -0.10  0.15 -0.06  0.07 -0.02 0.72 0.28 1.2
Q4_3   0.88 -0.02  0.00  0.17 -0.09 -0.18  0.10 0.74 0.26 1.2
Q4_4   0.79 -0.04  0.01  0.19  0.23 -0.25 -0.08 0.78 0.22 1.6
Q4_5   0.47  0.14  0.00  0.17 -0.06  0.16 -0.08 0.59 0.41 1.8
Q4_6   0.33  0.28  0.22  0.08  0.12 -0.22  0.08 0.53 0.47 4.3
Q4_7   0.14  0.28  0.18 -0.11  0.41 -0.19  0.01 0.42 0.58 3.2
Q4_8   0.79 -0.09  0.02 -0.06 -0.03  0.22 -0.06 0.69 0.31 1.2
Q4_9   0.58 -0.11 -0.06 -0.07  0.12  0.30  0.02 0.53 0.47 1.7
Q4_10  0.71 -0.05  0.09 -0.05  0.28 -0.08 -0.04 0.68 0.32 1.4
Q4_11  0.57 -0.03  0.00 -0.03  0.10  0.29  0.05 0.67 0.33 1.6
Q4_12  0.29 -0.07  0.18 -0.31  0.13  0.70 -0.05 0.69 0.31 2.1
Q4_13  0.34 -0.05  0.09 -0.12 -0.20  0.77  0.00 0.72 0.28 1.6
Q4_14  0.35  0.06  0.11 -0.12 -0.05  0.47  0.19 0.63 0.37 2.6
Q4_15  0.55  0.11 -0.02 -0.05 -0.06  0.38  0.00 0.69 0.31 1.9
Q4_16  0.55  0.25  0.19 -0.07 -0.16  0.10  0.00 0.60 0.40 2.0
Q4_17  0.59 -0.10  0.03 -0.04  0.09  0.28 -0.08 0.57 0.43 1.6
Q4_18  0.78  0.07 -0.13  0.02  0.00  0.24 -0.12 0.84 0.16 1.3
Q4_19  0.55  0.01 -0.05 -0.09  0.14  0.38 -0.01 0.70 0.30 2.0
Q5_1   0.13  0.40 -0.21  0.23 -0.10  0.31  0.04 0.57 0.43 3.7
Q5_2  -0.03  0.66  0.04 -0.05  0.03  0.16 -0.04 0.56 0.44 1.2
Q5_3  -0.03  0.75 -0.08  0.08 -0.24  0.32 -0.01 0.69 0.31 1.7
Q5_4   0.01  0.93 -0.02 -0.12  0.16 -0.24  0.00 0.69 0.31 1.2
Q5_5   0.04  0.89 -0.06 -0.07  0.13 -0.33  0.01 0.62 0.38 1.3
Q5_6   0.05  0.80 -0.03  0.02  0.04 -0.01 -0.06 0.70 0.30 1.0
Q5_7  -0.09  0.34  0.23 -0.09  0.20  0.30 -0.08 0.53 0.47 4.0
Q5_8  -0.12  0.77  0.00  0.05  0.11  0.06 -0.08 0.66 0.34 1.1
Q5_9   0.03  0.53  0.07  0.24 -0.09  0.16 -0.07 0.68 0.32 1.8
Q5_10  0.04  0.38 -0.03  0.10  0.13  0.24 -0.19 0.50 0.50 2.7
Q5_11  0.12  0.25  0.04  0.32 -0.06  0.08  0.23 0.56 0.44 3.3
Q5_12 -0.03  0.43  0.06  0.20  0.14  0.03  0.01 0.51 0.49 1.7
Q6_1   0.00 -0.02  0.82  0.11 -0.33  0.14  0.20 0.77 0.23 1.6
Q6_2  -0.03  0.06  0.99  0.00 -0.10 -0.10  0.08 0.83 0.17 1.1
Q6_3  -0.01  0.07  0.95 -0.12  0.01 -0.03 -0.01 0.81 0.19 1.0
Q6_4  -0.01  0.01  0.91 -0.07  0.00 -0.06 -0.06 0.69 0.31 1.0
Q6_5  -0.03 -0.03  0.22  0.29 -0.06  0.21  0.16 0.36 0.64 3.6
Q6_6  -0.03 -0.11  0.57  0.27  0.09  0.19 -0.17 0.77 0.23 2.0
Q6_7   0.07 -0.16  0.61  0.05  0.12  0.30 -0.08 0.79 0.21 1.8
Q6_8  -0.07 -0.17  0.64  0.17  0.11  0.25 -0.10 0.77 0.23 1.8
Q6_9  -0.07 -0.18  0.01 -0.01  0.21  0.65  0.29 0.53 0.47 1.9
Q6_10 -0.04  0.04  0.09  0.25  0.11  0.24  0.17 0.42 0.58 3.6
Q6_11 -0.05  0.13  0.22  0.07  0.30  0.24  0.05 0.60 0.40 3.6
Q7_1  -0.02  0.16  0.12  0.64  0.03 -0.01  0.06 0.74 0.26 1.2
Q7_2   0.00  0.10  0.05  0.28  0.42  0.05 -0.03 0.59 0.41 1.9
Q7_3  -0.07  0.13  0.04 -0.21  0.85 -0.02  0.15 0.69 0.31 1.3
Q7_4  -0.06 -0.04  0.06  0.50  0.63 -0.25 -0.13 0.66 0.34 2.4
Q7_5   0.06 -0.10 -0.06  0.35  0.55  0.09  0.06 0.70 0.30 1.9
Q7_6   0.06 -0.02  0.07  0.00  0.51  0.22  0.14 0.60 0.40 1.6
Q7_7   0.05  0.15 -0.17 -0.22  0.77  0.11  0.27 0.77 0.23 1.7
Q7_8   0.01 -0.05 -0.20  0.29  0.57  0.17  0.00 0.60 0.40 2.0
Q7_9   0.12  0.03  0.00  0.84 -0.04 -0.12  0.06 0.71 0.29 1.1
Q7_10  0.20 -0.04  0.07  0.87 -0.01 -0.17 -0.07 0.77 0.23 1.2
Q7_11  0.17 -0.09 -0.07  0.57  0.35 -0.12  0.06 0.63 0.37 2.1
Q7_12 -0.02 -0.03 -0.03  0.17  0.25  0.16  0.56 0.63 0.37 1.8
Q7_13 -0.08 -0.13  0.02 -0.04  0.26  0.09  0.72 0.59 0.41 1.4
Q7_14 -0.03  0.18 -0.05 -0.11  0.57 -0.14  0.35 0.52 0.48 2.2
Q7_15  0.12  0.01  0.03  0.82 -0.01 -0.16  0.00 0.64 0.36 1.1

                       PA3  PA4  PA2  PA5  PA6  PA1  PA7
SS loadings           8.79 5.81 5.50 5.13 5.28 4.72 1.75
Proportion Var        0.15 0.10 0.10 0.09 0.09 0.08 0.03
Cumulative Var        0.15 0.26 0.35 0.44 0.54 0.62 0.65
Proportion Explained  0.24 0.16 0.15 0.14 0.14 0.13 0.05
Cumulative Proportion 0.24 0.39 0.54 0.68 0.83 0.95 1.00

 With factor correlations of 
     PA3  PA4  PA2  PA5  PA6  PA1  PA7
PA3 1.00 0.62 0.52 0.66 0.55 0.61 0.20
PA4 0.62 1.00 0.52 0.66 0.61 0.59 0.30
PA2 0.52 0.52 1.00 0.63 0.46 0.65 0.04
PA5 0.66 0.66 0.63 1.00 0.63 0.75 0.22
PA6 0.55 0.61 0.46 0.63 1.00 0.55 0.28
PA1 0.61 0.59 0.65 0.75 0.55 1.00 0.13
PA7 0.20 0.30 0.04 0.22 0.28 0.13 1.00

Mean item complexity =  1.9
Test of the hypothesis that 7 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1218  and the objective function was  37.91 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 1

print(fit$loadings, cutoff=0.3)

Loadings:
      PA3    PA4    PA2    PA5    PA6    PA1    PA7   
Q4_1   0.876                                          
Q4_2   0.769                                          
Q4_3   0.881                                          
Q4_4   0.787                                          
Q4_5   0.474                                          
Q4_6   0.326                                          
Q4_7                               0.411              
Q4_8   0.786                                          
Q4_9   0.585                                          
Q4_10  0.711                                          
Q4_11  0.569                                          
Q4_12                      -0.315         0.697       
Q4_13  0.342                              0.768       
Q4_14  0.354                              0.472       
Q4_15  0.555                              0.381       
Q4_16  0.552                                          
Q4_17  0.585                                          
Q4_18  0.778                                          
Q4_19  0.547                              0.384       
Q5_1          0.396                       0.311       
Q5_2          0.665                                   
Q5_3          0.750                       0.325       
Q5_4          0.931                                   
Q5_5          0.890                      -0.331       
Q5_6          0.798                                   
Q5_7          0.336                       0.300       
Q5_8          0.766                                   
Q5_9          0.530                                   
Q5_10         0.375                                   
Q5_11                       0.325                     
Q5_12         0.427                                   
Q6_1                 0.815        -0.327              
Q6_2                 0.991                            
Q6_3                 0.952                            
Q6_4                 0.907                            
Q6_5                                                  
Q6_6                 0.572                            
Q6_7                 0.606                            
Q6_8                 0.645                            
Q6_9                                      0.646       
Q6_10                                                 
Q6_11                                                 
Q7_1                        0.639                     
Q7_2                               0.425              
Q7_3                               0.848              
Q7_4                        0.503  0.628              
Q7_5                        0.348  0.553              
Q7_6                               0.514              
Q7_7                               0.766              
Q7_8                               0.568              
Q7_9                        0.837                     
Q7_10                       0.868                     
Q7_11                       0.574  0.347              
Q7_12                                            0.556
Q7_13                                            0.718
Q7_14                              0.568         0.353
Q7_15                       0.815                     

                 PA3   PA4   PA2   PA5   PA6   PA1   PA7
SS loadings    7.292 5.403 5.036 4.454 4.354 3.879 1.550
Proportion Var 0.128 0.095 0.088 0.078 0.076 0.068 0.027
Cumulative Var 0.128 0.223 0.311 0.389 0.466 0.534 0.561

fit <- psych::fa(r = cov.dat, nfactors = 7, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 7, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA4   PA5   PA3   PA6   PA2   PA7   h2   u2   H2   U2
Q4_1   0.70  0.02  0.24 -0.01 -0.24 -0.12  0.06 0.48 0.27 0.64 0.36
Q4_2   0.66  0.01  0.12 -0.06 -0.07 -0.05  0.00 0.43 0.24 0.64 0.36
Q4_3   0.68  0.01  0.17 -0.01 -0.22 -0.05  0.09 0.45 0.25 0.65 0.35
Q4_4   0.58 -0.01  0.17  0.00 -0.26  0.18 -0.06 0.44 0.22 0.67 0.33
Q4_5   0.46  0.08  0.16  0.01  0.02 -0.07 -0.05 0.41 0.37 0.52 0.48
Q4_6   0.27  0.27  0.11  0.18 -0.15  0.10  0.06 0.44 0.53 0.45 0.55
Q4_7   0.14  0.26 -0.10  0.12 -0.11  0.36 -0.01 0.32 0.56 0.37 0.63
Q4_8   0.77 -0.07 -0.04  0.03  0.04 -0.04 -0.04 0.53 0.33 0.62 0.38
Q4_9   0.68 -0.12 -0.09 -0.05  0.17  0.12  0.00 0.50 0.52 0.49 0.51
Q4_10  0.54 -0.02  0.00  0.05 -0.13  0.19 -0.02 0.35 0.27 0.56 0.44
Q4_11  0.61 -0.04  0.00 -0.01  0.19  0.06  0.03 0.56 0.36 0.61 0.39
Q4_12  0.47 -0.10 -0.31  0.18  0.54  0.10 -0.07 0.65 0.46 0.59 0.41
Q4_13  0.44 -0.06 -0.15  0.12  0.41 -0.15  0.00 0.40 0.37 0.52 0.48
Q4_14  0.40  0.05 -0.09  0.04  0.37 -0.03  0.13 0.44 0.36 0.55 0.45
Q4_15  0.59  0.08 -0.03 -0.03  0.23 -0.08  0.00 0.53 0.31 0.63 0.37
Q4_16  0.55  0.23 -0.03  0.12 -0.02 -0.13 -0.01 0.47 0.41 0.53 0.47
Q4_17  0.63 -0.13 -0.03  0.05  0.13  0.06 -0.07 0.47 0.46 0.51 0.49
Q4_18  0.69  0.03  0.03 -0.08  0.03 -0.02 -0.08 0.50 0.18 0.74 0.26
Q4_19  0.64  0.00 -0.09 -0.07  0.24  0.12 -0.04 0.60 0.34 0.64 0.36
Q5_1   0.17  0.33  0.22 -0.20  0.27 -0.11  0.05 0.46 0.45 0.51 0.49
Q5_2   0.01  0.66 -0.05  0.01  0.10  0.07 -0.08 0.57 0.50 0.53 0.47
Q5_3   0.05  0.72  0.06 -0.11  0.29 -0.24 -0.02 0.68 0.41 0.62 0.38
Q5_4   0.00  1.04 -0.14  0.05 -0.34  0.16  0.02 0.81 0.41 0.66 0.34
Q5_5   0.00  0.96 -0.09  0.01 -0.41  0.14  0.03 0.66 0.41 0.62 0.38
Q5_6   0.04  0.70  0.03 -0.03 -0.04  0.04 -0.07 0.54 0.28 0.66 0.34
Q5_7  -0.04  0.30 -0.06  0.16  0.27  0.12 -0.07 0.42 0.46 0.48 0.52
Q5_8  -0.10  0.75  0.08 -0.01  0.04  0.07 -0.08 0.68 0.43 0.61 0.39
Q5_9   0.04  0.46  0.28  0.03  0.16 -0.13 -0.05 0.62 0.37 0.62 0.38
Q5_10  0.07  0.29  0.08 -0.02  0.11  0.08 -0.14 0.30 0.40 0.43 0.57
Q5_11  0.13  0.19  0.35  0.02  0.13 -0.09  0.21 0.46 0.45 0.51 0.49
Q5_12  0.00  0.36  0.19  0.05  0.03  0.13  0.00 0.43 0.48 0.47 0.53
Q6_1   0.01  0.01  0.05  0.65  0.08 -0.21  0.14 0.44 0.27 0.62 0.38
Q6_2  -0.04  0.06  0.02  0.88 -0.12 -0.05  0.07 0.63 0.20 0.76 0.24
Q6_3  -0.04  0.09 -0.09  0.88 -0.10  0.00  0.03 0.61 0.24 0.72 0.28
Q6_4  -0.01  0.03 -0.04  0.81 -0.14  0.03 -0.06 0.53 0.33 0.62 0.38
Q6_5  -0.02 -0.04  0.28  0.19  0.28 -0.09  0.20 0.32 0.74 0.30 0.70
Q6_6   0.01 -0.10  0.17  0.48  0.09  0.03 -0.09 0.43 0.24 0.64 0.36
Q6_7   0.09 -0.14  0.06  0.50  0.20  0.06 -0.05 0.53 0.24 0.69 0.31
Q6_8  -0.02 -0.18  0.16  0.54  0.20  0.05 -0.09 0.56 0.26 0.68 0.32
Q6_9   0.04 -0.25 -0.04 -0.06  0.97  0.16  0.33 0.72 0.77 0.48 0.52
Q6_10 -0.02  0.01  0.22  0.03  0.36  0.06  0.14 0.34 0.50 0.40 0.60
Q6_11 -0.03  0.11  0.07  0.15  0.33  0.26  0.03 0.53 0.41 0.56 0.44
Q7_1  -0.02  0.11  0.58  0.08  0.03  0.00  0.04 0.54 0.28 0.66 0.34
Q7_2   0.00  0.09  0.25  0.03  0.04  0.32 -0.05 0.40 0.34 0.54 0.46
Q7_3  -0.05  0.13 -0.19  0.05  0.07  0.81  0.10 0.67 0.35 0.66 0.34
Q7_4  -0.09 -0.08  0.51  0.05 -0.19  0.57 -0.18 0.60 0.36 0.63 0.37
Q7_5   0.06 -0.13  0.36 -0.07  0.14  0.49  0.00 0.60 0.30 0.66 0.34
Q7_6   0.08 -0.04  0.01  0.05  0.25  0.47  0.06 0.47 0.37 0.56 0.44
Q7_7   0.09  0.14 -0.21 -0.11  0.16  0.74  0.18 0.70 0.33 0.68 0.32
Q7_8   0.05 -0.08  0.23 -0.14  0.17  0.45 -0.04 0.42 0.35 0.55 0.45
Q7_9   0.08 -0.02  0.85 -0.02 -0.08 -0.05  0.03 0.64 0.35 0.65 0.35
Q7_10  0.15 -0.10  0.82  0.07 -0.14 -0.06 -0.06 0.61 0.29 0.68 0.32
Q7_11  0.11 -0.06  0.48 -0.04 -0.09  0.25  0.05 0.39 0.31 0.56 0.44
Q7_12 -0.01  0.02  0.19  0.00  0.28  0.23  0.49 0.56 0.49 0.53 0.47
Q7_13 -0.07 -0.08 -0.07  0.02  0.41  0.19  0.69 0.54 0.44 0.55 0.45
Q7_14 -0.05  0.22 -0.12 -0.01  0.04  0.52  0.29 0.46 0.51 0.47 0.53
Q7_15  0.07 -0.04  0.74  0.00 -0.08 -0.04 -0.01 0.47 0.35 0.57 0.43

                       PA1  PA4  PA5  PA3  PA6  PA2  PA7
SS loadings           7.37 5.16 4.31 3.89 3.38 4.08 1.10
Proportion Var        0.15 0.10 0.08 0.08 0.07 0.08 0.02
Cumulative Var        0.15 0.25 0.33 0.41 0.47 0.56 0.58
Proportion Explained  0.25 0.18 0.15 0.13 0.12 0.14 0.04
Cumulative Proportion 0.25 0.43 0.57 0.71 0.82 0.96 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA4   PA5   PA3   PA6   PA2   PA7   h2   u2
Q4_1     1  0.80  0.02  0.27 -0.01 -0.27 -0.13  0.07 0.64 0.36
Q4_2     2  0.80  0.01  0.15 -0.08 -0.08 -0.06 -0.01 0.64 0.36
Q4_3     3  0.82  0.01  0.21 -0.01 -0.26 -0.06  0.10 0.65 0.35
Q4_4     4  0.71 -0.01  0.21  0.00 -0.31  0.22 -0.07 0.67 0.33
Q4_5     5  0.53  0.09  0.18  0.02  0.02 -0.08 -0.06 0.52 0.48
Q4_6     6  0.27  0.27  0.11  0.18 -0.15  0.11  0.07 0.45 0.55
Q4_7     7  0.15  0.27 -0.11  0.13 -0.12  0.38 -0.01 0.37 0.63
Q4_8     8  0.83 -0.08 -0.04  0.03  0.05 -0.04 -0.05 0.62 0.38
Q4_9     9  0.68 -0.11 -0.09 -0.05  0.17  0.12  0.00 0.49 0.51
Q4_10   10  0.68 -0.03  0.00  0.07 -0.17  0.24 -0.02 0.56 0.44
Q4_11   11  0.64 -0.04  0.00 -0.01  0.20  0.07  0.04 0.61 0.39
Q4_12   12  0.44 -0.09 -0.30  0.17  0.51  0.10 -0.06 0.59 0.41
Q4_13   13  0.50 -0.07 -0.17  0.14  0.46 -0.17  0.00 0.52 0.48
Q4_14   14  0.44  0.06 -0.10  0.04  0.42 -0.03  0.15 0.55 0.45
Q4_15   15  0.65  0.08 -0.03 -0.03  0.25 -0.08  0.00 0.63 0.37
Q4_16   16  0.58  0.24 -0.03  0.13 -0.02 -0.14 -0.01 0.53 0.47
Q4_17   17  0.66 -0.13 -0.03  0.05  0.13  0.06 -0.07 0.51 0.49
Q4_18   18  0.84  0.03  0.04 -0.10  0.04 -0.02 -0.10 0.74 0.26
Q4_19   19  0.66  0.00 -0.09 -0.07  0.24  0.13 -0.05 0.64 0.36
Q5_1    20  0.18  0.34  0.23 -0.21  0.28 -0.12  0.05 0.51 0.49
Q5_2    21  0.01  0.64 -0.05  0.01  0.10  0.07 -0.07 0.53 0.47
Q5_3    22  0.05  0.69  0.06 -0.10  0.27 -0.23 -0.02 0.62 0.38
Q5_4    23  0.00  0.94 -0.13  0.05 -0.31  0.15  0.02 0.66 0.34
Q5_5    24  0.00  0.93 -0.08  0.01 -0.39  0.13  0.03 0.62 0.38
Q5_6    25  0.04  0.78  0.03 -0.03 -0.05  0.04 -0.07 0.66 0.34
Q5_7    26 -0.04  0.32 -0.07  0.17  0.29  0.13 -0.07 0.48 0.52
Q5_8    27 -0.09  0.71  0.08 -0.01  0.04  0.07 -0.07 0.61 0.39
Q5_9    28  0.04  0.46  0.28  0.03  0.16 -0.13 -0.05 0.62 0.38
Q5_10   29  0.08  0.34  0.10 -0.03  0.13  0.10 -0.17 0.43 0.57
Q5_11   30  0.14  0.19  0.37  0.03  0.14 -0.09  0.22 0.51 0.49
Q5_12   31  0.00  0.38  0.20  0.05  0.03  0.14  0.00 0.47 0.53
Q6_1    32  0.01  0.02  0.06  0.77  0.10 -0.25  0.16 0.62 0.38
Q6_2    33 -0.04  0.06  0.02  0.97 -0.13 -0.06  0.07 0.76 0.24
Q6_3    34 -0.04  0.09 -0.10  0.95 -0.11  0.00  0.03 0.72 0.28
Q6_4    35 -0.02  0.03 -0.05  0.88 -0.16  0.03 -0.07 0.62 0.38
Q6_5    36 -0.01 -0.04  0.27  0.18  0.27 -0.09  0.20 0.30 0.70
Q6_6    37  0.01 -0.12  0.21  0.58  0.11  0.03 -0.11 0.64 0.36
Q6_7    38  0.11 -0.16  0.07  0.57  0.23  0.07 -0.06 0.69 0.31
Q6_8    39 -0.03 -0.20  0.18  0.60  0.23  0.06 -0.09 0.68 0.32
Q6_9    40  0.03 -0.21 -0.04 -0.05  0.80  0.13  0.27 0.48 0.52
Q6_10   41 -0.03  0.01  0.25  0.03  0.39  0.06  0.15 0.40 0.60
Q6_11   42 -0.03  0.12  0.07  0.15  0.34  0.26  0.03 0.56 0.44
Q7_1    43 -0.03  0.13  0.65  0.09  0.04  0.00  0.05 0.66 0.34
Q7_2    44  0.00  0.10  0.29  0.03  0.05  0.38 -0.06 0.54 0.46
Q7_3    45 -0.05  0.13 -0.19  0.05  0.07  0.80  0.10 0.66 0.34
Q7_4    46 -0.09 -0.08  0.52  0.05 -0.20  0.58 -0.18 0.63 0.37
Q7_5    47  0.06 -0.14  0.38 -0.08  0.14  0.51  0.00 0.66 0.34
Q7_6    48  0.09 -0.04  0.01  0.05  0.27  0.51  0.07 0.56 0.44
Q7_7    49  0.09  0.14 -0.21 -0.10  0.16  0.73  0.18 0.68 0.32
Q7_8    50  0.06 -0.09  0.26 -0.16  0.20  0.51 -0.04 0.55 0.45
Q7_9    51  0.08 -0.02  0.86 -0.02 -0.08 -0.05  0.03 0.65 0.35
Q7_10   52  0.16 -0.11  0.87  0.08 -0.15 -0.07 -0.06 0.68 0.32
Q7_11   53  0.14 -0.07  0.58 -0.05 -0.11  0.29  0.06 0.56 0.44
Q7_12   54 -0.01  0.02  0.18  0.00  0.28  0.23  0.48 0.53 0.47
Q7_13   55 -0.07 -0.08 -0.07  0.02  0.42  0.19  0.70 0.55 0.45
Q7_14   56 -0.05  0.22 -0.12 -0.01  0.04  0.52  0.30 0.47 0.53
Q7_15   57  0.08 -0.04  0.82  0.00 -0.09 -0.05 -0.01 0.57 0.43

                 PA1  PA4  PA5  PA3  PA6  PA2  PA7
SS loadings     8.27 5.80 4.84 4.36 3.80 4.58 1.24
Proportion Var  0.15 0.10 0.08 0.08 0.07 0.08 0.02
Cumulative Var  0.15 0.25 0.33 0.41 0.47 0.56 0.58
Cum. factor Var 0.25 0.43 0.57 0.71 0.82 0.96 1.00

 With factor correlations of 
      PA1  PA4   PA5   PA3   PA6  PA2   PA7
PA1  1.00 0.63  0.71  0.54  0.62 0.52 -0.05
PA4  0.63 1.00  0.71  0.51  0.63 0.58  0.00
PA5  0.71 0.71  1.00  0.63  0.73 0.62 -0.05
PA3  0.54 0.51  0.63  1.00  0.66 0.38 -0.22
PA6  0.62 0.63  0.73  0.66  1.00 0.48 -0.25
PA2  0.52 0.58  0.62  0.38  0.48 1.00  0.12
PA7 -0.05 0.00 -0.05 -0.22 -0.25 0.12  1.00

Mean item complexity =  1.8
Test of the hypothesis that 7 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1218  and the objective function was  8.01 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   PA1  PA4  PA5  PA3  PA6  PA2
Correlation of (regression) scores with factors   0.98 0.97 0.97 0.97 0.94 0.95
Multiple R square of scores with factors          0.96 0.93 0.93 0.94 0.89 0.91
Minimum correlation of possible factor scores     0.91 0.87 0.87 0.88 0.78 0.82
                                                   PA7
Correlation of (regression) scores with factors   0.85
Multiple R square of scores with factors          0.72
Minimum correlation of possible factor scores     0.45

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA4    PA5    PA3    PA6    PA2    PA7   
Q4_1   0.696                                          
Q4_2   0.659                                          
Q4_3   0.684                                          
Q4_4   0.581                                          
Q4_5   0.463                                          
Q4_6                                                  
Q4_7                                      0.358       
Q4_8   0.767                                          
Q4_9   0.683                                          
Q4_10  0.539                                          
Q4_11  0.611                                          
Q4_12  0.466        -0.311         0.536              
Q4_13  0.441                       0.407              
Q4_14  0.397                       0.374              
Q4_15  0.593                                          
Q4_16  0.545                                          
Q4_17  0.633                                          
Q4_18  0.688                                          
Q4_19  0.642                                          
Q5_1          0.327                                   
Q5_2          0.657                                   
Q5_3          0.720                                   
Q5_4          1.039               -0.340              
Q5_5          0.964               -0.407              
Q5_6          0.703                                   
Q5_7          0.302                                   
Q5_8          0.754                                   
Q5_9          0.456                                   
Q5_10                                                 
Q5_11                0.352                            
Q5_12         0.362                                   
Q6_1                        0.650                     
Q6_2                        0.884                     
Q6_3                        0.876                     
Q6_4                        0.811                     
Q6_5                                                  
Q6_6                        0.478                     
Q6_7                        0.502                     
Q6_8                        0.541                     
Q6_9                               0.974         0.331
Q6_10                              0.357              
Q6_11                              0.327              
Q7_1                 0.583                            
Q7_2                                      0.325       
Q7_3                                      0.809       
Q7_4                 0.510                0.568       
Q7_5                 0.358                0.487       
Q7_6                                      0.466       
Q7_7                                      0.744       
Q7_8                                      0.449       
Q7_9                 0.850                            
Q7_10                0.818                            
Q7_11                0.483                            
Q7_12                                            0.492
Q7_13                              0.414         0.694
Q7_14                                     0.515       
Q7_15                0.738                            

                 PA1   PA4   PA5   PA3   PA6   PA2   PA7
SS loadings    6.428 5.245 4.021 3.747 3.475 3.388 1.268
Proportion Var 0.113 0.092 0.071 0.066 0.061 0.059 0.022
Cumulative Var 0.113 0.205 0.275 0.341 0.402 0.461 0.484

Eight factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 8, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 8, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA3   PA4   PA2   PA6   PA1   PA5   PA7   PA8   h2   u2 com
Q4_1   0.86 -0.03 -0.01 -0.17 -0.17  0.23  0.07  0.15 0.74 0.26 1.4
Q4_2   0.77 -0.02 -0.14 -0.07  0.10  0.18 -0.04  0.13 0.73 0.27 1.3
Q4_3   0.89  0.03  0.03 -0.08 -0.25  0.13  0.12  0.02 0.75 0.25 1.3
Q4_4   0.78 -0.04  0.00  0.24 -0.24  0.17 -0.08  0.14 0.78 0.22 1.6
Q4_5   0.47  0.04 -0.07 -0.07  0.24  0.23 -0.11  0.17 0.62 0.38 2.6
Q4_6   0.30  0.09  0.09  0.01 -0.04  0.20  0.05  0.51 0.69 0.31 2.2
Q4_7   0.12  0.13  0.08  0.32 -0.03 -0.03 -0.02  0.41 0.50 0.50 2.4
Q4_8   0.79 -0.08  0.03 -0.02  0.19 -0.06 -0.06  0.03 0.69 0.31 1.2
Q4_9   0.63  0.01  0.03  0.16  0.16 -0.15  0.06 -0.19 0.58 0.42 1.6
Q4_10  0.71 -0.04  0.09  0.26 -0.09 -0.06 -0.03  0.11 0.67 0.33 1.4
Q4_11  0.58 -0.04  0.00  0.09  0.28 -0.02  0.05  0.03 0.67 0.33 1.5
Q4_12  0.30 -0.13  0.13  0.10  0.74 -0.27 -0.05  0.04 0.70 0.30 1.8
Q4_13  0.37 -0.05  0.10 -0.19  0.73 -0.11  0.00 -0.12 0.72 0.28 1.8
Q4_14  0.36  0.02  0.09 -0.10  0.50 -0.08  0.18  0.05 0.63 0.37 2.4
Q4_15  0.58  0.15  0.02 -0.04  0.31 -0.07  0.01 -0.09 0.70 0.30 1.8
Q4_16  0.56  0.25  0.19 -0.18  0.07 -0.06  0.00  0.05 0.60 0.40 2.0
Q4_17  0.60 -0.09  0.04  0.10  0.24 -0.05 -0.08 -0.01 0.57 0.43 1.5
Q4_18  0.78  0.05 -0.14  0.01  0.23  0.03 -0.13  0.05 0.84 0.16 1.3
Q4_19  0.57  0.06 -0.02  0.15  0.31 -0.12  0.01 -0.08 0.70 0.30 1.9
Q5_1   0.15  0.40 -0.19 -0.07  0.28  0.22  0.05 -0.08 0.57 0.43 3.6
Q5_2  -0.04  0.59 -0.01 -0.01  0.23  0.00 -0.05  0.14 0.57 0.43 1.4
Q5_3  -0.02  0.71 -0.09 -0.24  0.33  0.10 -0.02  0.00 0.69 0.31 1.8
Q5_4   0.01  0.96  0.00  0.10 -0.27 -0.13  0.02  0.09 0.70 0.30 1.2
Q5_5   0.05  1.02  0.03  0.10 -0.46 -0.13  0.04 -0.03 0.68 0.32 1.5
Q5_6   0.06  0.84  0.01  0.04 -0.07  0.00 -0.05 -0.02 0.71 0.29 1.0
Q5_7  -0.08  0.35  0.24  0.20  0.28 -0.11 -0.07 -0.03 0.53 0.47 4.0
Q5_8  -0.11  0.77  0.01  0.11  0.04  0.04 -0.06  0.01 0.66 0.34 1.1
Q5_9   0.03  0.48  0.04 -0.07  0.19  0.26 -0.08  0.06 0.68 0.32 2.1
Q5_10  0.06  0.38 -0.01  0.17  0.21  0.07 -0.18 -0.05 0.50 0.50 2.7
Q5_11  0.13  0.26  0.05 -0.05  0.06  0.30  0.24 -0.02 0.56 0.44 3.6
Q5_12 -0.03  0.42  0.06  0.14  0.03  0.18  0.01  0.04 0.51 0.49 1.7
Q6_1   0.00 -0.01  0.81 -0.33  0.13  0.12  0.19  0.01 0.77 0.23 1.6
Q6_2  -0.04  0.07  0.98 -0.12 -0.09  0.00  0.08  0.11 0.83 0.17 1.1
Q6_3  -0.01  0.10  0.95 -0.01 -0.04 -0.13 -0.01  0.07 0.81 0.19 1.1
Q6_4  -0.01  0.07  0.94  0.01 -0.12 -0.11 -0.05  0.00 0.71 0.29 1.1
Q6_5  -0.03 -0.02  0.23 -0.03  0.20  0.26  0.16 -0.06 0.36 0.64 3.8
Q6_6  -0.02 -0.11  0.56  0.16  0.18  0.23 -0.17 -0.01 0.77 0.23 2.1
Q6_7   0.08 -0.14  0.61  0.15  0.28  0.02 -0.07 -0.03 0.79 0.21 1.8
Q6_8  -0.07 -0.15  0.65  0.16  0.23  0.13 -0.09 -0.05 0.77 0.23 1.7
Q6_9  -0.07 -0.25 -0.03  0.18  0.72  0.02  0.28  0.00 0.54 0.46 1.7
Q6_10 -0.06 -0.06  0.02  0.09  0.35  0.29  0.16  0.13 0.45 0.55 3.0
Q6_11 -0.08 -0.03  0.10  0.25  0.43  0.15  0.03  0.28 0.68 0.32 3.0
Q7_1  -0.02  0.13  0.10  0.09  0.02  0.61  0.06  0.04 0.74 0.26 1.2
Q7_2   0.01  0.12  0.06  0.46  0.04  0.22 -0.01 -0.01 0.59 0.41 1.7
Q7_3  -0.08  0.10  0.02  0.75  0.06 -0.22  0.18  0.18 0.69 0.31 1.5
Q7_4  -0.07 -0.05  0.05  0.68 -0.20  0.43 -0.11  0.09 0.66 0.34 2.1
Q7_5   0.06 -0.09 -0.05  0.58  0.10  0.28  0.08  0.00 0.70 0.30 1.7
Q7_6   0.07  0.03  0.10  0.50  0.19 -0.06  0.17 -0.05 0.61 0.39 1.8
Q7_7   0.06  0.14 -0.18  0.66  0.17 -0.23  0.30  0.12 0.77 0.23 2.2
Q7_8   0.03  0.03 -0.13  0.64  0.09  0.18  0.03 -0.17 0.63 0.37 1.5
Q7_9   0.11  0.02 -0.01  0.06 -0.10  0.78  0.05  0.00 0.71 0.29 1.1
Q7_10  0.19 -0.06  0.05  0.10 -0.15  0.81 -0.08  0.03 0.77 0.23 1.3
Q7_11  0.20  0.07  0.05  0.48 -0.32  0.44  0.11 -0.26 0.75 0.25 4.0
Q7_12 -0.01  0.06  0.04  0.20  0.09  0.10  0.61 -0.13 0.67 0.33 1.4
Q7_13 -0.08 -0.14  0.00  0.13  0.14 -0.03  0.73  0.08 0.58 0.42 1.3
Q7_14 -0.04  0.15 -0.07  0.45 -0.06 -0.09  0.37  0.19 0.53 0.47 2.8
Q7_15  0.10 -0.09 -0.04  0.07 -0.07  0.83 -0.03  0.14 0.67 0.33 1.1

                       PA3  PA4  PA2  PA6  PA1  PA5  PA7  PA8
SS loadings           8.93 5.64 5.35 5.24 4.80 4.67 1.95 1.22
Proportion Var        0.16 0.10 0.09 0.09 0.08 0.08 0.03 0.02
Cumulative Var        0.16 0.26 0.35 0.44 0.53 0.61 0.64 0.66
Proportion Explained  0.24 0.15 0.14 0.14 0.13 0.12 0.05 0.03
Cumulative Proportion 0.24 0.39 0.53 0.67 0.79 0.92 0.97 1.00

 With factor correlations of 
     PA3  PA4  PA2  PA6  PA1  PA5  PA7  PA8
PA3 1.00 0.61 0.52 0.55 0.63 0.66 0.21 0.11
PA4 0.61 1.00 0.50 0.60 0.66 0.67 0.30 0.28
PA2 0.52 0.50 1.00 0.45 0.67 0.63 0.04 0.12
PA6 0.55 0.60 0.45 1.00 0.57 0.58 0.34 0.21
PA1 0.63 0.66 0.67 0.57 1.00 0.74 0.17 0.14
PA5 0.66 0.67 0.63 0.58 0.74 1.00 0.25 0.12
PA7 0.21 0.30 0.04 0.34 0.17 0.25 1.00 0.13
PA8 0.11 0.28 0.12 0.21 0.14 0.12 0.13 1.00

Mean item complexity =  1.9
Test of the hypothesis that 8 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1168  and the objective function was  37.08 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.04 

Fit based upon off diagonal values = 1

print(fit$loadings, cutoff=0.3)

Loadings:
      PA3    PA4    PA2    PA6    PA1    PA5    PA7    PA8   
Q4_1   0.865                                                 
Q4_2   0.766                                                 
Q4_3   0.888                                                 
Q4_4   0.779                                                 
Q4_5   0.465                                                 
Q4_6                                                    0.509
Q4_7                        0.320                       0.411
Q4_8   0.794                                                 
Q4_9   0.628                                                 
Q4_10  0.710                                                 
Q4_11  0.579                                                 
Q4_12  0.304                       0.743                     
Q4_13  0.368                       0.726                     
Q4_14  0.360                       0.502                     
Q4_15  0.576                       0.305                     
Q4_16  0.555                                                 
Q4_17  0.597                                                 
Q4_18  0.783                                                 
Q4_19  0.572                       0.315                     
Q5_1          0.395                                          
Q5_2          0.588                                          
Q5_3          0.706                0.327                     
Q5_4          0.961                                          
Q5_5          1.023               -0.455                     
Q5_6          0.840                                          
Q5_7          0.346                                          
Q5_8          0.771                                          
Q5_9          0.478                                          
Q5_10         0.381                                          
Q5_11                                                        
Q5_12         0.419                                          
Q6_1                 0.810 -0.330                            
Q6_2                 0.976                                   
Q6_3                 0.951                                   
Q6_4                 0.941                                   
Q6_5                                                         
Q6_6                 0.561                                   
Q6_7                 0.606                                   
Q6_8                 0.647                                   
Q6_9                               0.718                     
Q6_10                              0.353                     
Q6_11                              0.431                     
Q7_1                                      0.606              
Q7_2                        0.459                            
Q7_3                        0.746                            
Q7_4                        0.681         0.435              
Q7_5                        0.584                            
Q7_6                        0.500                            
Q7_7                        0.659                            
Q7_8                        0.642                            
Q7_9                                      0.777              
Q7_10                                     0.809              
Q7_11                       0.478 -0.318  0.440              
Q7_12                                            0.615       
Q7_13                                            0.731       
Q7_14                       0.451                0.373       
Q7_15                                     0.827              

                 PA3   PA4   PA2   PA6   PA1   PA5   PA7   PA8
SS loadings    7.439 5.444 4.910 4.094 4.060 3.933 1.689 0.998
Proportion Var 0.131 0.096 0.086 0.072 0.071 0.069 0.030 0.018
Cumulative Var 0.131 0.226 0.312 0.384 0.455 0.524 0.554 0.571

fit <- psych::fa(r = cov.dat, nfactors = 8, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 8, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA4   PA5   PA6   PA3   PA2   PA7   PA8   h2   u2   H2   U2
Q4_1   0.66 -0.02  0.25 -0.22 -0.03 -0.12  0.06  0.16 0.48 0.27 0.65 0.35
Q4_2   0.63 -0.03  0.13 -0.05 -0.08 -0.05 -0.01  0.11 0.43 0.24 0.65 0.35
Q4_3   0.67  0.05  0.17 -0.24 -0.01 -0.06  0.09  0.05 0.45 0.25 0.65 0.35
Q4_4   0.56 -0.02  0.17 -0.25 -0.01  0.17 -0.06  0.12 0.44 0.22 0.67 0.33
Q4_5   0.43 -0.01  0.18  0.06 -0.01 -0.06 -0.06  0.15 0.42 0.36 0.54 0.46
Q4_6   0.20  0.02  0.18 -0.03  0.10  0.11  0.05  0.50 0.60 0.36 0.63 0.37
Q4_7   0.09  0.08 -0.07 -0.02  0.06  0.38 -0.03  0.36 0.40 0.48 0.46 0.54
Q4_8   0.76 -0.06 -0.04  0.03  0.03 -0.04 -0.04  0.02 0.53 0.33 0.62 0.38
Q4_9   0.73  0.02 -0.14  0.08  0.00  0.11  0.01 -0.18 0.54 0.47 0.54 0.46
Q4_10  0.52 -0.03  0.00 -0.13  0.04  0.19 -0.02  0.10 0.35 0.27 0.56 0.44
Q4_11  0.60 -0.04  0.00  0.19 -0.01  0.06  0.03  0.04 0.56 0.36 0.61 0.39
Q4_12  0.47 -0.13 -0.30  0.55  0.18  0.10 -0.07  0.01 0.65 0.46 0.58 0.42
Q4_13  0.46 -0.03 -0.15  0.38  0.14 -0.15  0.01 -0.09 0.41 0.36 0.53 0.47
Q4_14  0.39  0.01 -0.08  0.40  0.03 -0.03  0.12  0.05 0.44 0.36 0.55 0.45
Q4_15  0.60  0.11 -0.04  0.20 -0.01 -0.08  0.00 -0.06 0.53 0.31 0.64 0.36
Q4_16  0.53  0.21 -0.02 -0.02  0.12 -0.13 -0.02  0.08 0.47 0.42 0.53 0.47
Q4_17  0.63 -0.10 -0.03  0.10  0.06  0.06 -0.07 -0.01 0.47 0.46 0.51 0.49
Q4_18  0.67  0.00  0.04  0.04 -0.09 -0.01 -0.08  0.06 0.50 0.18 0.74 0.26
Q4_19  0.66  0.05 -0.10  0.20 -0.04  0.12 -0.04 -0.07 0.61 0.33 0.65 0.35
Q5_1   0.18  0.32  0.22  0.27 -0.19 -0.10  0.05 -0.04 0.46 0.45 0.51 0.49
Q5_2  -0.01  0.55 -0.03  0.16 -0.02  0.08 -0.09  0.15 0.58 0.49 0.54 0.46
Q5_3   0.05  0.65  0.07  0.31 -0.11 -0.23 -0.03  0.02 0.68 0.41 0.62 0.38
Q5_4   0.01  1.09 -0.16 -0.39  0.07  0.14  0.02  0.04 0.82 0.40 0.67 0.33
Q5_5   0.03  1.15 -0.13 -0.54  0.07  0.10  0.05 -0.10 0.75 0.32 0.70 0.30
Q5_6   0.05  0.72  0.02 -0.07 -0.02  0.03 -0.06 -0.02 0.54 0.28 0.66 0.34
Q5_7  -0.02  0.31 -0.07  0.26  0.18  0.12 -0.06 -0.05 0.42 0.46 0.48 0.52
Q5_8  -0.09  0.74  0.08  0.04  0.00  0.07 -0.07  0.01 0.68 0.44 0.61 0.39
Q5_9   0.03  0.37  0.30  0.20  0.01 -0.12 -0.06  0.08 0.62 0.37 0.63 0.37
Q5_10  0.07  0.28  0.08  0.11 -0.02  0.09 -0.14 -0.02 0.30 0.40 0.43 0.57
Q5_11  0.13  0.19  0.34  0.13  0.03 -0.09  0.21  0.00 0.46 0.45 0.51 0.49
Q5_12 -0.01  0.34  0.19  0.04  0.04  0.13  0.00  0.05 0.43 0.48 0.47 0.53
Q6_1   0.00  0.02  0.05  0.08  0.64 -0.21  0.14  0.04 0.44 0.28 0.61 0.39
Q6_2  -0.05  0.05  0.02 -0.12  0.86 -0.06  0.06  0.11 0.63 0.20 0.76 0.24
Q6_3  -0.04  0.11 -0.09 -0.10  0.86 -0.01  0.03  0.07 0.61 0.24 0.72 0.28
Q6_4   0.00  0.08 -0.05 -0.18  0.81  0.02 -0.06  0.01 0.54 0.32 0.63 0.37
Q6_5   0.00  0.00  0.26  0.26  0.21 -0.09  0.21 -0.07 0.33 0.74 0.31 0.69
Q6_6   0.02 -0.07  0.16  0.07  0.49  0.03 -0.08 -0.04 0.43 0.24 0.65 0.35
Q6_7   0.11 -0.11  0.05  0.18  0.51  0.06 -0.05 -0.05 0.53 0.24 0.69 0.31
Q6_8  -0.01 -0.15  0.15  0.18  0.55  0.06 -0.08 -0.07 0.56 0.25 0.69 0.31
Q6_9   0.05 -0.30 -0.04  1.00 -0.06  0.17  0.33 -0.03 0.72 0.78 0.48 0.52
Q6_10 -0.04 -0.07  0.24  0.40  0.01  0.07  0.14  0.07 0.34 0.49 0.41 0.59
Q6_11 -0.07 -0.06  0.10  0.44  0.09  0.27  0.01  0.23 0.58 0.36 0.62 0.38
Q7_1  -0.03  0.09  0.58  0.05  0.08  0.01  0.04  0.03 0.54 0.28 0.66 0.34
Q7_2   0.01  0.12  0.23  0.02  0.05  0.32 -0.04 -0.04 0.40 0.33 0.55 0.45
Q7_3  -0.06  0.09 -0.19  0.10  0.03  0.79  0.10  0.14 0.67 0.35 0.66 0.34
Q7_4  -0.10 -0.11  0.50 -0.17  0.05  0.58 -0.17  0.08 0.60 0.36 0.63 0.37
Q7_5   0.07 -0.11  0.34  0.13 -0.06  0.49  0.01 -0.02 0.60 0.30 0.66 0.34
Q7_6   0.10  0.00 -0.01  0.22  0.06  0.46  0.07 -0.05 0.48 0.37 0.57 0.43
Q7_7   0.09  0.15 -0.22  0.16 -0.10  0.72  0.18  0.05 0.70 0.33 0.68 0.32
Q7_8   0.08  0.01  0.20  0.12 -0.10  0.45 -0.02 -0.15 0.44 0.33 0.58 0.42
Q7_9   0.08 -0.03  0.84 -0.06 -0.02 -0.03  0.03  0.02 0.64 0.35 0.64 0.36
Q7_10  0.15 -0.11  0.80 -0.14  0.08 -0.04 -0.05  0.02 0.61 0.29 0.68 0.32
Q7_11  0.15  0.10  0.46 -0.21  0.02  0.24  0.07 -0.22 0.47 0.24 0.67 0.33
Q7_12  0.02  0.13  0.16  0.23  0.04  0.20  0.52 -0.11 0.60 0.45 0.57 0.43
Q7_13 -0.08 -0.09 -0.06  0.43  0.00  0.17  0.68  0.09 0.53 0.45 0.54 0.46
Q7_14 -0.07  0.16 -0.10  0.09 -0.04  0.50  0.29  0.19 0.47 0.50 0.49 0.51
Q7_15  0.04 -0.12  0.76 -0.03 -0.02 -0.02 -0.01  0.12 0.48 0.34 0.59 0.41

                       PA1  PA4  PA5  PA6  PA3  PA2  PA7  PA8
SS loadings           7.30 4.95 4.28 3.42 3.84 4.02 1.12 1.06
Proportion Var        0.14 0.10 0.08 0.07 0.08 0.08 0.02 0.02
Cumulative Var        0.14 0.24 0.33 0.39 0.47 0.55 0.57 0.59
Proportion Explained  0.24 0.17 0.14 0.11 0.13 0.13 0.04 0.04
Cumulative Proportion 0.24 0.41 0.55 0.67 0.79 0.93 0.96 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA4   PA5   PA6   PA3   PA2   PA7   PA8   h2   u2
Q4_1     1  0.76 -0.02  0.29 -0.25 -0.04 -0.13  0.07  0.18 0.65 0.35
Q4_2     2  0.77 -0.03  0.16 -0.06 -0.10 -0.06 -0.01  0.14 0.65 0.35
Q4_3     3  0.80  0.06  0.20 -0.28 -0.01 -0.07  0.10  0.06 0.65 0.35
Q4_4     4  0.68 -0.03  0.21 -0.31 -0.02  0.21 -0.07  0.14 0.67 0.33
Q4_5     5  0.49 -0.01  0.21  0.07 -0.02 -0.07 -0.07  0.17 0.54 0.46
Q4_6     6  0.20  0.02  0.18 -0.03  0.10  0.11  0.05  0.51 0.63 0.37
Q4_7     7  0.10  0.09 -0.08 -0.02  0.07  0.40 -0.03  0.38 0.46 0.54
Q4_8     8  0.82 -0.06 -0.04  0.03  0.04 -0.04 -0.05  0.02 0.62 0.38
Q4_9     9  0.73  0.02 -0.14  0.08  0.00  0.11  0.01 -0.18 0.54 0.46
Q4_10   10  0.66 -0.04  0.00 -0.17  0.05  0.23 -0.02  0.13 0.56 0.44
Q4_11   11  0.63 -0.05  0.00  0.20 -0.01  0.07  0.04  0.04 0.61 0.39
Q4_12   12  0.45 -0.13 -0.29  0.52  0.17  0.10 -0.06  0.01 0.58 0.42
Q4_13   13  0.52 -0.03 -0.18  0.43  0.16 -0.17  0.01 -0.10 0.53 0.47
Q4_14   14  0.43  0.01 -0.09  0.44  0.03 -0.03  0.14  0.06 0.55 0.45
Q4_15   15  0.66  0.12 -0.04  0.21 -0.01 -0.09  0.01 -0.06 0.64 0.36
Q4_16   16  0.56  0.22 -0.02 -0.02  0.12 -0.14 -0.02  0.08 0.53 0.47
Q4_17   17  0.66 -0.11 -0.03  0.11  0.06  0.06 -0.07 -0.01 0.51 0.49
Q4_18   18  0.82  0.00  0.05  0.05 -0.11 -0.02 -0.10  0.07 0.74 0.26
Q4_19   19  0.68  0.05 -0.11  0.20 -0.05  0.12 -0.04 -0.07 0.65 0.35
Q5_1    20  0.19  0.33  0.23  0.28 -0.20 -0.11  0.05 -0.04 0.51 0.49
Q5_2    21 -0.01  0.53 -0.03  0.16 -0.02  0.07 -0.08  0.14 0.54 0.46
Q5_3    22  0.05  0.63  0.07  0.30 -0.11 -0.22 -0.03  0.02 0.62 0.38
Q5_4    23  0.01  0.99 -0.14 -0.35  0.06  0.13  0.02  0.04 0.67 0.33
Q5_5    24  0.03  1.11 -0.13 -0.52  0.06  0.10  0.05 -0.10 0.70 0.30
Q5_6    25  0.06  0.80  0.03 -0.07 -0.02  0.04 -0.07 -0.03 0.66 0.34
Q5_7    26 -0.02  0.33 -0.07  0.27  0.19  0.13 -0.07 -0.05 0.48 0.52
Q5_8    27 -0.08  0.70  0.08  0.03  0.00  0.07 -0.07  0.01 0.61 0.39
Q5_9    28  0.03  0.38  0.30  0.20  0.01 -0.12 -0.06  0.08 0.63 0.37
Q5_10   29  0.09  0.33  0.10  0.13 -0.02  0.10 -0.17 -0.02 0.43 0.57
Q5_11   30  0.14  0.20  0.36  0.14  0.03 -0.09  0.22  0.01 0.51 0.49
Q5_12   31 -0.01  0.35  0.20  0.05  0.04  0.14  0.00  0.05 0.47 0.53
Q6_1    32  0.00  0.02  0.06  0.10  0.76 -0.25  0.16  0.05 0.61 0.39
Q6_2    33 -0.05  0.06  0.02 -0.13  0.94 -0.07  0.07  0.12 0.76 0.24
Q6_3    34 -0.04  0.11 -0.10 -0.11  0.93 -0.02  0.03  0.08 0.72 0.28
Q6_4    35  0.00  0.09 -0.06 -0.19  0.88  0.02 -0.06  0.01 0.63 0.37
Q6_5    36  0.00  0.00  0.26  0.25  0.20 -0.09  0.20 -0.07 0.31 0.69
Q6_6    37  0.03 -0.08  0.20  0.09  0.60  0.04 -0.10 -0.05 0.65 0.35
Q6_7    38  0.12 -0.12  0.05  0.21  0.59  0.07 -0.06 -0.06 0.69 0.31
Q6_8    39 -0.01 -0.17  0.16  0.20  0.61  0.06 -0.09 -0.07 0.69 0.31
Q6_9    40  0.04 -0.25 -0.03  0.82 -0.05  0.14  0.27 -0.03 0.48 0.52
Q6_10   41 -0.04 -0.07  0.26  0.44  0.01  0.07  0.15  0.08 0.41 0.59
Q6_11   42 -0.07 -0.06  0.10  0.46  0.10  0.28  0.01  0.24 0.62 0.38
Q7_1    43 -0.03  0.10  0.64  0.06  0.09  0.01  0.05  0.04 0.66 0.34
Q7_2    44  0.02  0.14  0.27  0.02  0.05  0.38 -0.05 -0.05 0.55 0.45
Q7_3    45 -0.06  0.09 -0.18  0.10  0.03  0.78  0.10  0.13 0.66 0.34
Q7_4    46 -0.10 -0.11  0.51 -0.17  0.05  0.59 -0.17  0.08 0.63 0.37
Q7_5    47  0.07 -0.12  0.36  0.14 -0.06  0.52  0.01 -0.02 0.66 0.34
Q7_6    48  0.11  0.00 -0.01  0.24  0.07  0.50  0.08 -0.06 0.57 0.43
Q7_7    49  0.09  0.15 -0.22  0.16 -0.10  0.71  0.18  0.05 0.68 0.32
Q7_8    50  0.09  0.01  0.23  0.14 -0.12  0.52 -0.03 -0.18 0.58 0.42
Q7_9    51  0.08 -0.03  0.84 -0.06 -0.02 -0.03  0.03  0.02 0.64 0.36
Q7_10   52  0.15 -0.11  0.85 -0.14  0.08 -0.05 -0.06  0.02 0.68 0.32
Q7_11   53  0.18  0.12  0.55 -0.25  0.03  0.29  0.08 -0.27 0.67 0.33
Q7_12   54  0.02  0.13  0.15  0.22  0.04  0.20  0.51 -0.11 0.57 0.43
Q7_13   55 -0.08 -0.09 -0.06  0.44  0.00  0.17  0.69  0.09 0.54 0.46
Q7_14   56 -0.08  0.16 -0.10  0.09 -0.04  0.50  0.29  0.19 0.49 0.51
Q7_15   57  0.05 -0.13  0.83 -0.03 -0.03 -0.03 -0.01  0.13 0.59 0.41

                 PA1  PA4  PA5  PA6  PA3  PA2  PA7  PA8
SS loadings     8.20 5.56 4.80 3.84 4.31 4.52 1.25 1.19
Proportion Var  0.14 0.10 0.08 0.07 0.08 0.08 0.02 0.02
Cumulative Var  0.14 0.24 0.33 0.39 0.47 0.55 0.57 0.59
Cum. factor Var 0.24 0.41 0.55 0.67 0.79 0.93 0.96 1.00

 With factor correlations of 
      PA1   PA4   PA5   PA6   PA3  PA2   PA7   PA8
PA1  1.00  0.61  0.71  0.63  0.53 0.51 -0.06  0.25
PA4  0.61  1.00  0.71  0.68  0.48 0.57 -0.06  0.40
PA5  0.71  0.71  1.00  0.74  0.62 0.61 -0.07  0.24
PA6  0.63  0.68  0.74  1.00  0.66 0.48 -0.25  0.25
PA3  0.53  0.48  0.62  0.66  1.00 0.37 -0.22  0.18
PA2  0.51  0.57  0.61  0.48  0.37 1.00  0.12  0.16
PA7 -0.06 -0.06 -0.07 -0.25 -0.22 0.12  1.00 -0.05
PA8  0.25  0.40  0.24  0.25  0.18 0.16 -0.05  1.00

Mean item complexity =  1.9
Test of the hypothesis that 8 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1168  and the objective function was  7.45 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   PA1  PA4  PA5  PA6  PA3  PA2
Correlation of (regression) scores with factors   0.98 0.97 0.97 0.95 0.97 0.95
Multiple R square of scores with factors          0.96 0.94 0.93 0.90 0.94 0.91
Minimum correlation of possible factor scores     0.91 0.87 0.87 0.80 0.88 0.82
                                                   PA7  PA8
Correlation of (regression) scores with factors   0.86 0.84
Multiple R square of scores with factors          0.73 0.71
Minimum correlation of possible factor scores     0.46 0.42

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA4    PA5    PA6    PA3    PA2    PA7    PA8   
Q4_1   0.661                                                 
Q4_2   0.635                                                 
Q4_3   0.670                                                 
Q4_4   0.558                                                 
Q4_5   0.435                                                 
Q4_6                                                    0.502
Q4_7                                      0.375         0.357
Q4_8   0.760                                                 
Q4_9   0.731                                                 
Q4_10  0.522                                                 
Q4_11  0.604                                                 
Q4_12  0.469        -0.303  0.546                            
Q4_13  0.458                0.381                            
Q4_14  0.388                0.395                            
Q4_15  0.603                                                 
Q4_16  0.531                                                 
Q4_17  0.634                                                 
Q4_18  0.672                                                 
Q4_19  0.659                                                 
Q5_1          0.315                                          
Q5_2          0.550                                          
Q5_3          0.655         0.309                            
Q5_4          1.092        -0.387                            
Q5_5          1.151        -0.541                            
Q5_6          0.724                                          
Q5_7          0.308                                          
Q5_8          0.737                                          
Q5_9          0.374  0.303                                   
Q5_10                                                        
Q5_11                0.344                                   
Q5_12         0.336                                          
Q6_1                               0.637                     
Q6_2                               0.860                     
Q6_3                               0.860                     
Q6_4                               0.815                     
Q6_5                                                         
Q6_6                               0.488                     
Q6_7                               0.513                     
Q6_8                               0.554                     
Q6_9         -0.303         1.002                0.328       
Q6_10                       0.404                            
Q6_11                       0.443                            
Q7_1                 0.578                                   
Q7_2                                      0.324              
Q7_3                                      0.790              
Q7_4                 0.502                0.575              
Q7_5                 0.341                0.489              
Q7_6                                      0.458              
Q7_7                                      0.721              
Q7_8                                      0.452              
Q7_9                 0.836                                   
Q7_10                0.804                                   
Q7_11                0.458                                   
Q7_12                                            0.522       
Q7_13                       0.434                0.685       
Q7_14                                     0.498              
Q7_15                0.756                                   

                 PA1   PA4   PA5   PA6   PA3   PA2   PA7   PA8
SS loadings    6.305 5.305 3.971 3.734 3.659 3.287 1.281 0.844
Proportion Var 0.111 0.093 0.070 0.066 0.064 0.058 0.022 0.015
Cumulative Var 0.111 0.204 0.273 0.339 0.403 0.461 0.483 0.498

Nine factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 9, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 9, rotate = "Promax", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA3   PA4   PA2   PA9   PA6   PA5   PA1   PA7   PA8   h2   u2 com
Q4_1   0.95 -0.03 -0.01 -0.13 -0.17  0.20 -0.07  0.07  0.15 0.73 0.27 1.3
Q4_2   0.81 -0.02 -0.12 -0.14  0.01  0.21  0.17 -0.04  0.14 0.74 0.26 1.4
Q4_3   0.98  0.03  0.03 -0.23 -0.10  0.11 -0.09  0.11  0.02 0.74 0.26 1.2
Q4_4   0.86 -0.04 -0.01 -0.12  0.18  0.14 -0.14 -0.08  0.13 0.78 0.22 1.3
Q4_5   0.48  0.04 -0.05  0.00  0.02  0.27  0.23 -0.11  0.18 0.64 0.36 2.6
Q4_6   0.34  0.09  0.10  0.11  0.13  0.19 -0.08  0.04  0.50 0.68 0.32 2.7
Q4_7   0.16  0.13  0.06  0.29  0.33 -0.08 -0.20 -0.03  0.40 0.51 0.49 4.3
Q4_8   0.85 -0.08  0.02 -0.01 -0.02 -0.04  0.13 -0.05  0.03 0.68 0.32 1.1
Q4_9   0.65  0.01  0.05 -0.26  0.20 -0.07  0.25  0.04 -0.20 0.60 0.40 2.2
Q4_10  0.80 -0.05  0.07  0.01  0.20 -0.08 -0.11 -0.04  0.09 0.68 0.32 1.3
Q4_11  0.63 -0.04 -0.02  0.24  0.05 -0.05  0.07  0.05  0.02 0.67 0.33 1.4
Q4_12  0.27 -0.12  0.15  0.19  0.25 -0.17  0.52 -0.08  0.05 0.75 0.25 3.1
Q4_13  0.30 -0.03  0.14 -0.09  0.01  0.03  0.74 -0.02 -0.12 0.89 0.11 1.5
Q4_14  0.39  0.02  0.07  0.47 -0.11 -0.12  0.13  0.19  0.06 0.64 0.36 2.9
Q4_15  0.65  0.14 -0.02  0.35 -0.16 -0.15  0.02  0.03 -0.09 0.73 0.27 2.0
Q4_16  0.65  0.24  0.15  0.26 -0.28 -0.15 -0.13  0.02  0.06 0.65 0.35 2.5
Q4_17  0.66 -0.09  0.02  0.20  0.03 -0.08  0.05 -0.07 -0.02 0.58 0.42 1.3
Q4_18  0.84  0.05 -0.14  0.08 -0.01  0.03  0.13 -0.12  0.05 0.84 0.16 1.2
Q4_19  0.60  0.06 -0.01  0.03  0.16 -0.08  0.22  0.00 -0.08 0.70 0.30 1.5
Q5_1   0.14  0.39 -0.17  0.15 -0.07  0.21  0.17  0.05 -0.07 0.57 0.43 3.4
Q5_2  -0.07  0.59  0.02  0.02  0.11  0.06  0.21 -0.07  0.15 0.59 0.41 1.6
Q5_3  -0.06  0.70 -0.06  0.10 -0.16  0.13  0.25 -0.02  0.01 0.70 0.30 1.5
Q5_4   0.01  0.92  0.01 -0.25  0.18 -0.09 -0.05  0.00  0.09 0.70 0.30 1.3
Q5_5   0.05  0.98  0.04 -0.40  0.15 -0.10 -0.11  0.03 -0.04 0.67 0.33 1.4
Q5_6   0.09  0.81 -0.01  0.10 -0.02 -0.05 -0.09 -0.04 -0.02 0.72 0.28 1.1
Q5_7  -0.07  0.33  0.19  0.54  0.06 -0.20 -0.07 -0.06 -0.04 0.58 0.42 2.5
Q5_8  -0.11  0.74  0.00  0.19  0.06  0.00 -0.04 -0.06  0.01 0.67 0.33 1.2
Q5_9   0.05  0.46  0.01  0.45 -0.18  0.16 -0.06 -0.06  0.06 0.71 0.29 2.7
Q5_10  0.07  0.37 -0.04  0.34  0.04  0.01 -0.01 -0.17 -0.06 0.52 0.48 2.6
Q5_11  0.14  0.25  0.05  0.12 -0.06  0.26  0.01  0.23 -0.01 0.56 0.44 4.2
Q5_12 -0.04  0.41  0.07  0.06  0.15  0.18  0.03  0.01  0.03 0.51 0.49 1.8
Q6_1  -0.02  0.00  0.81  0.00 -0.25  0.14  0.15  0.19  0.02 0.78 0.22 1.5
Q6_2  -0.05  0.07  0.98 -0.14 -0.03  0.05  0.05  0.07  0.11 0.85 0.15 1.1
Q6_3  -0.02  0.09  0.93 -0.08  0.04 -0.08  0.04 -0.01  0.07 0.81 0.19 1.1
Q6_4   0.00  0.07  0.92 -0.11  0.02 -0.08 -0.01 -0.04  0.00 0.71 0.29 1.1
Q6_5  -0.04 -0.02  0.21  0.22 -0.05  0.23  0.08  0.16 -0.06 0.36 0.64 4.4
Q6_6  -0.03 -0.11  0.53  0.25  0.07  0.21  0.05 -0.16 -0.02 0.77 0.23 2.2
Q6_7   0.10 -0.14  0.56  0.39  0.04 -0.02  0.02 -0.06 -0.03 0.80 0.20 2.1
Q6_8  -0.06 -0.16  0.60  0.41  0.03  0.07 -0.02 -0.08 -0.05 0.79 0.21 2.1
Q6_9  -0.07 -0.25 -0.07  0.83  0.10 -0.06  0.12  0.29  0.00 0.57 0.43 1.6
Q6_10 -0.03 -0.08 -0.05  0.83 -0.07  0.15 -0.15  0.18  0.14 0.53 0.47 1.4
Q6_11 -0.07 -0.03  0.07  0.70  0.20  0.08 -0.02  0.02  0.28 0.70 0.30 1.6
Q7_1  -0.04  0.14  0.12  0.03  0.09  0.60  0.08  0.05  0.03 0.75 0.25 1.3
Q7_2  -0.01  0.12  0.07  0.01  0.44  0.24  0.06 -0.03 -0.03 0.60 0.40 1.9
Q7_3  -0.10  0.10  0.05 -0.04  0.88 -0.13  0.07  0.13  0.15 0.72 0.28 1.2
Q7_4  -0.08 -0.04  0.06 -0.08  0.64  0.45 -0.07 -0.13  0.06 0.67 0.33 2.1
Q7_5   0.07 -0.09 -0.05  0.17  0.52  0.27  0.00  0.07 -0.03 0.70 0.30 1.9
Q7_6   0.06  0.03  0.11  0.06  0.52 -0.01  0.12  0.15 -0.07 0.61 0.39 1.5
Q7_7   0.04  0.14 -0.15  0.02  0.79 -0.15  0.11  0.25  0.10 0.79 0.21 1.5
Q7_8   0.03  0.03 -0.14  0.18  0.51  0.16 -0.02  0.02 -0.19 0.63 0.37 2.0
Q7_9   0.12  0.02  0.01  0.00  0.01  0.73 -0.01  0.06 -0.01 0.71 0.29 1.1
Q7_10  0.20 -0.05  0.07 -0.11  0.05  0.79  0.02 -0.08  0.02 0.78 0.22 1.2
Q7_11  0.25  0.06  0.03 -0.02  0.26  0.36 -0.23  0.12 -0.31 0.78 0.22 4.9
Q7_12 -0.01  0.05  0.04  0.14  0.22  0.08  0.00  0.59 -0.14 0.67 0.33 1.6
Q7_13 -0.08 -0.13  0.00  0.29  0.21 -0.06 -0.07  0.70  0.07 0.58 0.42 1.7
Q7_14 -0.03  0.15 -0.07  0.08  0.52 -0.08 -0.11  0.34  0.16 0.52 0.48 2.4
Q7_15  0.11 -0.08 -0.03  0.13  0.00  0.75 -0.06 -0.02  0.14 0.67 0.33 1.2

                       PA3  PA4  PA2  PA9  PA6  PA5  PA1  PA7  PA8
SS loadings           9.71 5.47 5.15 4.87 4.84 4.27 1.94 1.67 0.68
Proportion Var        0.17 0.10 0.09 0.09 0.08 0.07 0.03 0.03 0.01
Cumulative Var        0.17 0.27 0.36 0.44 0.53 0.60 0.64 0.67 0.68
Proportion Explained  0.25 0.14 0.13 0.13 0.13 0.11 0.05 0.04 0.02
Cumulative Proportion 0.25 0.39 0.53 0.65 0.78 0.89 0.94 0.98 1.00

 With factor correlations of 
      PA3   PA4   PA2   PA9   PA6   PA5   PA1   PA7   PA8
PA3  1.00  0.64  0.54  0.72  0.58  0.68  0.43  0.12 -0.21
PA4  0.64  1.00  0.47  0.67  0.58  0.64  0.37  0.21 -0.04
PA2  0.54  0.47  1.00  0.67  0.41  0.58  0.41 -0.05 -0.16
PA9  0.72  0.67  0.67  1.00  0.64  0.73  0.52  0.06 -0.26
PA6  0.58  0.58  0.41  0.64  1.00  0.57  0.19  0.21 -0.19
PA5  0.68  0.64  0.58  0.73  0.57  1.00  0.40  0.16 -0.20
PA1  0.43  0.37  0.41  0.52  0.19  0.40  1.00  0.06 -0.02
PA7  0.12  0.21 -0.05  0.06  0.21  0.16  0.06  1.00  0.05
PA8 -0.21 -0.04 -0.16 -0.26 -0.19 -0.20 -0.02  0.05  1.00

Mean item complexity =  1.9
Test of the hypothesis that 9 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1119  and the objective function was  35.98 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 1

print(fit$loadings, cutoff=0.3)

Loadings:
      PA3    PA4    PA2    PA9    PA6    PA5    PA1    PA7    PA8   
Q4_1   0.951                                                        
Q4_2   0.812                                                        
Q4_3   0.977                                                        
Q4_4   0.865                                                        
Q4_5   0.476                                                        
Q4_6   0.339                                                   0.500
Q4_7                               0.330                       0.397
Q4_8   0.852                                                        
Q4_9   0.651                                                        
Q4_10  0.796                                                        
Q4_11  0.632                                                        
Q4_12                                            0.518              
Q4_13                                            0.737              
Q4_14  0.394                0.468                                   
Q4_15  0.649                0.347                                   
Q4_16  0.651                                                        
Q4_17  0.657                                                        
Q4_18  0.841                                                        
Q4_19  0.599                                                        
Q5_1          0.389                                                 
Q5_2          0.587                                                 
Q5_3          0.698                                                 
Q5_4          0.925                                                 
Q5_5          0.977        -0.398                                   
Q5_6          0.811                                                 
Q5_7          0.333         0.537                                   
Q5_8          0.744                                                 
Q5_9          0.464         0.451                                   
Q5_10         0.367         0.344                                   
Q5_11                                                               
Q5_12         0.410                                                 
Q6_1                 0.811                                          
Q6_2                 0.978                                          
Q6_3                 0.935                                          
Q6_4                 0.919                                          
Q6_5                                                                
Q6_6                 0.533                                          
Q6_7                 0.563  0.393                                   
Q6_8                 0.603  0.409                                   
Q6_9                        0.834                                   
Q6_10                       0.827                                   
Q6_11                       0.698                                   
Q7_1                                      0.598                     
Q7_2                               0.444                            
Q7_3                               0.878                            
Q7_4                               0.639  0.447                     
Q7_5                               0.520                            
Q7_6                               0.522                            
Q7_7                               0.788                            
Q7_8                               0.507                            
Q7_9                                      0.732                     
Q7_10                                     0.791                     
Q7_11                                     0.362               -0.309
Q7_12                                                   0.585       
Q7_13                                                   0.696       
Q7_14                              0.522                0.336       
Q7_15                                     0.754                     

                 PA3   PA4   PA2   PA9   PA6   PA5   PA1   PA7   PA8
SS loadings    8.753 5.119 4.663 4.310 4.018 3.395 1.535 1.527 1.010
Proportion Var 0.154 0.090 0.082 0.076 0.070 0.060 0.027 0.027 0.018
Cumulative Var 0.154 0.243 0.325 0.401 0.471 0.531 0.558 0.585 0.602

fit <- psych::fa(r = cov.dat, nfactors = 9, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 9, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA4   PA9   PA6   PA3   PA2   PA7   PA5   PA8   h2   u2   H2   U2
Q4_1   0.69  0.02 -0.15  0.21 -0.04 -0.14  0.05 -0.09  0.16 0.49 0.26 0.65 0.35
Q4_2   0.66 -0.03 -0.10  0.14 -0.07 -0.04 -0.01  0.02  0.11 0.43 0.24 0.65 0.35
Q4_3   0.70  0.10 -0.19  0.13 -0.02 -0.08  0.08 -0.11  0.05 0.45 0.25 0.65 0.35
Q4_4   0.58  0.04 -0.10  0.10 -0.04  0.11 -0.06 -0.18  0.12 0.46 0.21 0.69 0.31
Q4_5   0.46 -0.05 -0.01  0.20  0.00 -0.03 -0.06  0.10  0.15 0.42 0.35 0.54 0.46
Q4_6   0.22 -0.02 -0.03  0.18  0.11  0.13  0.04  0.06  0.49 0.59 0.37 0.62 0.38
Q4_7   0.10  0.07  0.08 -0.11  0.05  0.34 -0.03 -0.03  0.36 0.40 0.48 0.46 0.54
Q4_8   0.78 -0.04 -0.03 -0.03  0.03 -0.04 -0.04  0.01  0.02 0.53 0.33 0.61 0.39
Q4_9   0.76  0.00 -0.23 -0.02  0.04  0.21  0.02  0.15 -0.20 0.59 0.42 0.59 0.41
Q4_10  0.55  0.05  0.04 -0.09  0.01  0.10 -0.02 -0.19  0.10 0.38 0.25 0.60 0.40
Q4_11  0.63 -0.03  0.22 -0.04 -0.03  0.03  0.03 -0.02  0.04 0.56 0.35 0.61 0.39
Q4_12  0.48 -0.20  0.32 -0.23  0.19  0.16 -0.06  0.23  0.01 0.66 0.45 0.60 0.40
Q4_13  0.47 -0.10  0.12 -0.06  0.17 -0.07  0.01  0.24 -0.09 0.43 0.34 0.56 0.44
Q4_14  0.40 -0.01  0.37 -0.09  0.02 -0.04  0.12  0.09  0.05 0.44 0.36 0.55 0.45
Q4_15  0.62  0.11  0.24 -0.08 -0.03 -0.12  0.01  0.03 -0.06 0.54 0.30 0.64 0.36
Q4_16  0.55  0.20  0.05 -0.06  0.10 -0.16 -0.02  0.02  0.08 0.47 0.41 0.54 0.46
Q4_17  0.65 -0.09  0.05 -0.03  0.05  0.06 -0.06  0.01 -0.01 0.47 0.46 0.51 0.49
Q4_18  0.70  0.01  0.06  0.01 -0.10 -0.04 -0.08  0.00  0.06 0.50 0.18 0.74 0.26
Q4_19  0.68  0.00 -0.01 -0.03 -0.02  0.18 -0.03  0.16 -0.08 0.63 0.31 0.67 0.33
Q5_1   0.19  0.20  0.17  0.26 -0.17 -0.06  0.05  0.25 -0.04 0.46 0.44 0.51 0.49
Q5_2  -0.01  0.35 -0.10  0.11  0.03  0.21 -0.09  0.45  0.16 0.66 0.41 0.62 0.38
Q5_3   0.04  0.43  0.03  0.23 -0.07 -0.10 -0.02  0.56  0.02 0.77 0.32 0.71 0.29
Q5_4   0.01  1.01 -0.21 -0.17  0.06  0.11  0.03  0.08  0.04 0.82 0.40 0.67 0.33
Q5_5   0.04  1.12 -0.29 -0.18  0.05  0.04  0.05 -0.02 -0.10 0.77 0.30 0.72 0.28
Q5_6   0.06  0.63  0.04  0.01 -0.02  0.02 -0.06  0.14 -0.02 0.54 0.28 0.66 0.34
Q5_7  -0.03  0.32  0.60 -0.23  0.11 -0.01 -0.07 -0.06 -0.05 0.50 0.39 0.56 0.44
Q5_8  -0.09  0.64  0.21  0.04 -0.02  0.03 -0.07  0.14  0.01 0.68 0.43 0.61 0.39
Q5_9   0.03  0.31  0.43  0.20 -0.03 -0.20 -0.06  0.09  0.08 0.65 0.34 0.65 0.35
Q5_10  0.08  0.24  0.27  0.01 -0.05  0.02 -0.14  0.03 -0.02 0.31 0.39 0.45 0.55
Q5_11  0.14  0.16  0.13  0.34  0.03 -0.07  0.21  0.08  0.00 0.46 0.45 0.51 0.49
Q5_12  0.00  0.25 -0.01  0.23  0.06  0.17  0.00  0.16  0.05 0.43 0.47 0.48 0.52
Q6_1   0.00 -0.01 -0.02  0.10  0.65 -0.16  0.13  0.09  0.04 0.45 0.26 0.63 0.37
Q6_2  -0.05  0.05 -0.19  0.07  0.87 -0.01  0.06  0.03  0.11 0.65 0.19 0.78 0.22
Q6_3  -0.04  0.12 -0.05 -0.09  0.84 -0.02  0.03 -0.05  0.07 0.61 0.25 0.71 0.29
Q6_4  -0.01  0.08 -0.23  0.00  0.82  0.06 -0.06  0.01  0.01 0.55 0.31 0.64 0.36
Q6_5   0.00  0.02  0.39  0.19  0.18 -0.14  0.21 -0.05 -0.07 0.34 0.72 0.32 0.68
Q6_6   0.02 -0.05  0.16  0.12  0.46  0.00 -0.08 -0.05 -0.04 0.44 0.24 0.65 0.35
Q6_7   0.11 -0.07  0.30 -0.01  0.48  0.01 -0.05 -0.07 -0.05 0.54 0.23 0.70 0.30
Q6_8  -0.01 -0.13  0.29  0.09  0.52  0.01 -0.08 -0.06 -0.06 0.57 0.25 0.70 0.30
Q6_9   0.05 -0.30  1.10 -0.13 -0.10  0.09  0.33  0.04 -0.03 0.75 0.74 0.50 0.50
Q6_10 -0.04 -0.06  0.62  0.13 -0.03 -0.03  0.14 -0.05  0.08 0.38 0.46 0.45 0.55
Q6_11 -0.07 -0.09  0.61  0.02  0.06  0.20  0.01  0.02  0.24 0.60 0.34 0.64 0.36
Q7_1  -0.02  0.03  0.04  0.58  0.09  0.04  0.05  0.09  0.03 0.54 0.27 0.66 0.34
Q7_2   0.01  0.11  0.09  0.20  0.04  0.30 -0.04 -0.02 -0.04 0.40 0.33 0.55 0.45
Q7_3  -0.06  0.08  0.04 -0.14  0.05  0.80  0.10 -0.01  0.14 0.68 0.35 0.66 0.34
Q7_4  -0.10 -0.11 -0.17  0.52  0.05  0.58 -0.17 -0.05  0.08 0.61 0.35 0.64 0.36
Q7_5   0.07 -0.11  0.12  0.34 -0.06  0.48  0.01 -0.02 -0.02 0.60 0.30 0.66 0.34
Q7_6   0.10 -0.01  0.13  0.04  0.07  0.48  0.08  0.05 -0.05 0.48 0.36 0.57 0.43
Q7_7   0.09  0.13  0.01 -0.14 -0.08  0.77  0.18  0.05  0.06 0.72 0.31 0.70 0.30
Q7_8   0.08  0.02  0.17  0.18 -0.12  0.41 -0.02 -0.05 -0.15 0.44 0.33 0.58 0.42
Q7_9   0.08 -0.09 -0.13  0.87  0.00  0.02  0.03  0.08  0.02 0.65 0.33 0.66 0.34
Q7_10  0.16 -0.14 -0.18  0.82  0.09 -0.01 -0.05  0.03  0.02 0.61 0.28 0.69 0.31
Q7_11  0.15  0.16 -0.07  0.40  0.00  0.19  0.07 -0.17 -0.22 0.47 0.23 0.67 0.33
Q7_12  0.01  0.16  0.22  0.16  0.04  0.21  0.51 -0.05 -0.11 0.60 0.44 0.57 0.43
Q7_13 -0.08 -0.05  0.38 -0.05  0.01  0.19  0.65 -0.04  0.09 0.51 0.47 0.52 0.48
Q7_14 -0.07  0.15  0.07 -0.08 -0.02  0.51  0.28 -0.01  0.19 0.47 0.50 0.49 0.51
Q7_15  0.06 -0.15 -0.01  0.73 -0.02 -0.01 -0.01  0.02  0.12 0.48 0.34 0.59 0.41

                       PA1  PA4  PA9  PA6  PA3  PA2  PA7  PA5  PA8
SS loadings           7.63 4.12 3.79 4.07 3.73 3.91 1.06 1.32 1.03
Proportion Var        0.15 0.08 0.07 0.08 0.07 0.08 0.02 0.03 0.02
Cumulative Var        0.15 0.23 0.31 0.39 0.46 0.54 0.56 0.58 0.60
Proportion Explained  0.25 0.13 0.12 0.13 0.12 0.13 0.03 0.04 0.03
Cumulative Proportion 0.25 0.38 0.51 0.64 0.76 0.89 0.92 0.97 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA4   PA9   PA6   PA3   PA2   PA7   PA5   PA8   h2   u2
Q4_1     1  0.80  0.02 -0.18  0.24 -0.05 -0.16  0.06 -0.11  0.18 0.65 0.35
Q4_2     2  0.81 -0.04 -0.12  0.17 -0.09 -0.05 -0.01  0.03  0.13 0.65 0.35
Q4_3     3  0.83  0.11 -0.22  0.16 -0.02 -0.10  0.10 -0.13  0.06 0.65 0.35
Q4_4     4  0.72  0.05 -0.12  0.12 -0.05  0.13 -0.07 -0.22  0.14 0.69 0.31
Q4_5     5  0.52 -0.05 -0.01  0.23  0.00 -0.04 -0.07  0.12  0.17 0.54 0.46
Q4_6     6  0.22 -0.02 -0.04  0.18  0.12  0.13  0.04  0.06  0.50 0.62 0.38
Q4_7     7  0.11  0.08  0.08 -0.12  0.06  0.36 -0.03 -0.04  0.38 0.46 0.54
Q4_8     8  0.85 -0.05 -0.03 -0.04  0.03 -0.04 -0.05  0.01  0.02 0.61 0.39
Q4_9     9  0.76  0.00 -0.23 -0.02  0.04  0.21  0.02  0.14 -0.20 0.59 0.41
Q4_10   10  0.70  0.06  0.05 -0.11  0.01  0.13 -0.03 -0.24  0.13 0.60 0.40
Q4_11   11  0.66 -0.03  0.23 -0.04 -0.03  0.03  0.03 -0.02  0.04 0.61 0.39
Q4_12   12  0.46 -0.19  0.30 -0.22  0.18  0.15 -0.06  0.22  0.01 0.60 0.40
Q4_13   13  0.54 -0.11  0.13 -0.07  0.19 -0.08  0.01  0.28 -0.11 0.56 0.44
Q4_14   14  0.45 -0.02  0.41 -0.10  0.02 -0.04  0.14  0.10  0.06 0.55 0.45
Q4_15   15  0.68  0.12  0.26 -0.09 -0.03 -0.13  0.01  0.03 -0.06 0.64 0.36
Q4_16   16  0.59  0.21  0.06 -0.06  0.10 -0.17 -0.02  0.02  0.08 0.54 0.46
Q4_17   17  0.68 -0.10  0.05 -0.03  0.05  0.06 -0.07  0.01 -0.01 0.51 0.49
Q4_18   18  0.85  0.01  0.07  0.01 -0.12 -0.05 -0.10  0.00  0.07 0.74 0.26
Q4_19   19  0.70  0.00 -0.01 -0.03 -0.02  0.18 -0.03  0.16 -0.08 0.67 0.33
Q5_1    20  0.20  0.21  0.18  0.28 -0.18 -0.06  0.05  0.26 -0.04 0.51 0.49
Q5_2    21 -0.01  0.34 -0.09  0.11  0.03  0.20 -0.09  0.43  0.16 0.62 0.38
Q5_3    22  0.04  0.41  0.03  0.22 -0.07 -0.10 -0.02  0.53  0.02 0.71 0.29
Q5_4    23  0.01  0.91 -0.19 -0.15  0.06  0.10  0.02  0.07  0.04 0.67 0.33
Q5_5    24  0.03  1.09 -0.28 -0.18  0.05  0.04  0.05 -0.02 -0.10 0.72 0.28
Q5_6    25  0.06  0.69  0.04  0.01 -0.03  0.02 -0.06  0.16 -0.02 0.66 0.34
Q5_7    26 -0.03  0.34  0.64 -0.24  0.12 -0.01 -0.08 -0.06 -0.06 0.56 0.44
Q5_8    27 -0.08  0.60  0.20  0.03 -0.02  0.03 -0.07  0.14  0.01 0.61 0.39
Q5_9    28  0.03  0.31  0.43  0.21 -0.03 -0.20 -0.06  0.09  0.08 0.65 0.35
Q5_10   29  0.09  0.29  0.33  0.02 -0.06  0.03 -0.17  0.04 -0.02 0.45 0.55
Q5_11   30  0.14  0.16  0.13  0.36  0.04 -0.08  0.22  0.08  0.00 0.51 0.49
Q5_12   31  0.00  0.26 -0.01  0.24  0.06  0.18  0.00  0.17  0.05 0.48 0.52
Q6_1    32  0.00 -0.01 -0.03  0.12  0.77 -0.18  0.16  0.11  0.05 0.63 0.37
Q6_2    33 -0.05  0.05 -0.21  0.08  0.96 -0.01  0.07  0.03  0.12 0.78 0.22
Q6_3    34 -0.04  0.13 -0.06 -0.09  0.91 -0.02  0.03 -0.05  0.08 0.71 0.29
Q6_4    35 -0.01  0.09 -0.25  0.00  0.88  0.07 -0.06  0.01  0.01 0.64 0.36
Q6_5    36  0.00  0.02  0.38  0.19  0.17 -0.14  0.20 -0.05 -0.07 0.32 0.68
Q6_6    37  0.03 -0.06  0.20  0.15  0.56 -0.01 -0.10 -0.06 -0.05 0.65 0.35
Q6_7    38  0.13 -0.08  0.35 -0.02  0.54  0.01 -0.06 -0.08 -0.06 0.70 0.30
Q6_8    39 -0.01 -0.14  0.32  0.10  0.57  0.01 -0.09 -0.07 -0.07 0.70 0.30
Q6_9    40  0.04 -0.25  0.90 -0.11 -0.09  0.07  0.27  0.03 -0.03 0.50 0.50
Q6_10   41 -0.04 -0.07  0.68  0.14 -0.04 -0.03  0.15 -0.05  0.09 0.45 0.55
Q6_11   42 -0.07 -0.09  0.63  0.02  0.06  0.21  0.01  0.02  0.25 0.64 0.36
Q7_1    43 -0.03  0.04  0.04  0.65  0.10  0.04  0.05  0.10  0.03 0.66 0.34
Q7_2    44  0.02  0.13  0.11  0.24  0.04  0.35 -0.04 -0.02 -0.05 0.55 0.45
Q7_3    45 -0.06  0.08  0.04 -0.14  0.05  0.79  0.10 -0.01  0.14 0.66 0.34
Q7_4    46 -0.10 -0.12 -0.17  0.53  0.06  0.60 -0.17 -0.05  0.08 0.64 0.36
Q7_5    47  0.07 -0.12  0.13  0.36 -0.06  0.51  0.01 -0.03 -0.02 0.66 0.34
Q7_6    48  0.11 -0.02  0.14  0.04  0.08  0.52  0.08  0.05 -0.05 0.57 0.43
Q7_7    49  0.09  0.13  0.01 -0.14 -0.08  0.76  0.18  0.05  0.06 0.70 0.30
Q7_8    50  0.09  0.02  0.20  0.20 -0.13  0.47 -0.02 -0.06 -0.17 0.58 0.42
Q7_9    51  0.08 -0.09 -0.13  0.88  0.00  0.02  0.03  0.08  0.02 0.66 0.34
Q7_10   52  0.17 -0.14 -0.19  0.87  0.10 -0.01 -0.05  0.03  0.02 0.69 0.31
Q7_11   53  0.18  0.19 -0.08  0.48  0.00  0.23  0.08 -0.20 -0.27 0.67 0.33
Q7_12   54  0.01  0.16  0.21  0.15  0.04  0.20  0.50 -0.05 -0.11 0.57 0.43
Q7_13   55 -0.08 -0.05  0.38 -0.06  0.01  0.19  0.66 -0.04  0.09 0.52 0.48
Q7_14   56 -0.07  0.16  0.07 -0.08 -0.02  0.51  0.29 -0.01  0.20 0.49 0.51
Q7_15   57  0.06 -0.16 -0.01  0.81 -0.02 -0.02 -0.01  0.03  0.13 0.59 0.41

                 PA1  PA4  PA9  PA6  PA3  PA2  PA7  PA5  PA8
SS loadings     8.56 4.63 4.25 4.57 4.19 4.39 1.19 1.49 1.16
Proportion Var  0.15 0.08 0.07 0.08 0.07 0.08 0.02 0.03 0.02
Cumulative Var  0.15 0.23 0.31 0.39 0.46 0.54 0.56 0.58 0.60
Cum. factor Var 0.25 0.38 0.51 0.64 0.76 0.89 0.92 0.97 1.00

 With factor correlations of 
      PA1   PA4   PA9   PA6   PA3  PA2   PA7   PA5   PA8
PA1  1.00  0.57  0.70  0.71  0.53 0.53 -0.09  0.27  0.20
PA4  0.57  1.00  0.64  0.69  0.38 0.58 -0.08  0.18  0.39
PA9  0.70  0.64  1.00  0.79  0.67 0.62 -0.21  0.32  0.20
PA6  0.71  0.69  0.79  1.00  0.58 0.61 -0.10  0.20  0.22
PA3  0.53  0.38  0.67  0.58  1.00 0.36 -0.23  0.30  0.10
PA2  0.53  0.58  0.62  0.61  0.36 1.00  0.04  0.13  0.15
PA7 -0.09 -0.08 -0.21 -0.10 -0.23 0.04  1.00 -0.04 -0.03
PA5  0.27  0.18  0.32  0.20  0.30 0.13 -0.04  1.00  0.05
PA8  0.20  0.39  0.20  0.22  0.10 0.15 -0.03  0.05  1.00

Mean item complexity =  1.9
Test of the hypothesis that 9 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1119  and the objective function was  6.84 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   PA1  PA4  PA9  PA6  PA3  PA2
Correlation of (regression) scores with factors   0.98 0.96 0.96 0.96 0.97 0.95
Multiple R square of scores with factors          0.96 0.92 0.92 0.93 0.94 0.91
Minimum correlation of possible factor scores     0.92 0.85 0.84 0.86 0.88 0.82
                                                   PA7  PA5  PA8
Correlation of (regression) scores with factors   0.85 0.86 0.84
Multiple R square of scores with factors          0.72 0.74 0.71
Minimum correlation of possible factor scores     0.44 0.49 0.42

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA4    PA9    PA6    PA3    PA2    PA7    PA5    PA8   
Q4_1   0.691                                                        
Q4_2   0.661                                                        
Q4_3   0.695                                                        
Q4_4   0.585                                                        
Q4_5   0.457                                                        
Q4_6                                                           0.492
Q4_7                                      0.340                0.358
Q4_8   0.785                                                        
Q4_9   0.762                                                        
Q4_10  0.549                                                        
Q4_11  0.626                                                        
Q4_12  0.484         0.316                                          
Q4_13  0.473                                                        
Q4_14  0.402         0.369                                          
Q4_15  0.623                                                        
Q4_16  0.553                                                        
Q4_17  0.652                                                        
Q4_18  0.699                                                        
Q4_19  0.681                                                        
Q5_1                                                                
Q5_2          0.353                                     0.446       
Q5_3          0.432                                     0.559       
Q5_4          1.010                                                 
Q5_5          1.122                                                 
Q5_6          0.628                                                 
Q5_7          0.319  0.604                                          
Q5_8          0.635                                                 
Q5_9          0.306  0.432                                          
Q5_10                                                               
Q5_11                       0.340                                   
Q5_12                                                               
Q6_1                               0.653                            
Q6_2                               0.874                            
Q6_3                               0.843                            
Q6_4                               0.818                            
Q6_5                 0.391                                          
Q6_6                               0.462                            
Q6_7                 0.304         0.476                            
Q6_8                               0.519                            
Q6_9         -0.304  1.099                       0.331              
Q6_10                0.623                                          
Q6_11                0.612                                          
Q7_1                        0.585                                   
Q7_2                                                                
Q7_3                                      0.804                     
Q7_4                        0.517         0.584                     
Q7_5                        0.341         0.482                     
Q7_6                                      0.481                     
Q7_7                                      0.769                     
Q7_8                                      0.414                     
Q7_9                        0.870                                   
Q7_10                       0.820                                   
Q7_11                       0.402                                   
Q7_12                                            0.511              
Q7_13                0.375                       0.651              
Q7_14                                     0.507                     
Q7_15                       0.735                                   

                 PA1   PA4   PA9   PA6   PA3   PA2   PA7   PA5   PA8
SS loadings    6.802 4.244 4.127 3.844 3.559 3.256 1.213 1.024 0.857
Proportion Var 0.119 0.074 0.072 0.067 0.062 0.057 0.021 0.018 0.015
Cumulative Var 0.119 0.194 0.266 0.334 0.396 0.453 0.474 0.492 0.507

Ten factor extraction

fit <- psych::fa(r = corr.pc$rho, nfactors = 10, rotate = "Promax", fm = "pa")

Warning in fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a
different factor score estimation method.

fit

Factor Analysis using method =  pa
Call: psych::fa(r = corr.pc$rho, nfactors = 10, rotate = "Promax", 
    fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
        PA3   PA2   PA6  PA10   PA4   PA5   PA9   PA7   PA1   PA8   h2    u2
Q4_1   0.96 -0.02 -0.18 -0.14  0.00  0.19 -0.05  0.08 -0.04  0.14 0.73 0.267
Q4_2   0.84 -0.12 -0.03 -0.10  0.02  0.19 -0.03 -0.03  0.18  0.12 0.75 0.245
Q4_3   0.99  0.02 -0.12 -0.21  0.07  0.11 -0.10  0.12 -0.05  0.02 0.74 0.257
Q4_4   0.89 -0.02  0.14 -0.06  0.03  0.12 -0.22 -0.07 -0.07  0.11 0.79 0.210
Q4_5   0.50 -0.05 -0.02  0.04  0.05  0.24  0.05 -0.10  0.22  0.17 0.65 0.353
Q4_6   0.33  0.11  0.15  0.04  0.03  0.20  0.13  0.03 -0.09  0.52 0.68 0.318
Q4_7   0.15  0.07  0.36  0.24  0.06 -0.07  0.05 -0.04 -0.20  0.42 0.52 0.482
Q4_8   0.85  0.02 -0.02 -0.01 -0.06 -0.04  0.00 -0.05  0.12  0.03 0.68 0.318
Q4_9   0.62  0.07  0.27 -0.34 -0.04 -0.03  0.17  0.02  0.17 -0.19 0.63 0.367
Q4_10  0.84  0.06  0.14  0.11  0.06 -0.12 -0.29 -0.01 -0.03  0.07 0.72 0.284
Q4_11  0.64 -0.02  0.05  0.24 -0.03 -0.05  0.00  0.05  0.07  0.02 0.67 0.328
Q4_12  0.29  0.14  0.21  0.25 -0.08 -0.20  0.05 -0.06  0.47  0.03 0.76 0.241
Q4_13  0.33  0.13 -0.04 -0.01  0.01 -0.01  0.12  0.00  0.69 -0.15 0.93 0.073
Q4_14  0.37  0.07 -0.06  0.36 -0.06 -0.10  0.24  0.18  0.06  0.07 0.65 0.349
Q4_15  0.63 -0.01 -0.12  0.28  0.04 -0.12  0.22  0.01 -0.04 -0.07 0.75 0.245
Q4_16  0.62  0.17 -0.22  0.16  0.09 -0.11  0.31  0.00 -0.22  0.10 0.72 0.275
Q4_17  0.63  0.03  0.08  0.12 -0.15 -0.05  0.14 -0.09 -0.01  0.01 0.60 0.402
Q4_18  0.86 -0.15 -0.04  0.12  0.06  0.02  0.00 -0.11  0.14  0.04 0.84 0.159
Q4_19  0.57  0.01  0.22 -0.04 -0.02 -0.05  0.21 -0.02  0.13 -0.06 0.72 0.275
Q5_1   0.14 -0.17 -0.06  0.15  0.27  0.21  0.24  0.05  0.13 -0.06 0.56 0.436
Q5_2  -0.13  0.04  0.20 -0.09  0.35  0.11  0.54 -0.10  0.10  0.20 0.66 0.342
Q5_3  -0.11 -0.05 -0.09  0.01  0.44  0.19  0.60 -0.05  0.14  0.05 0.75 0.253
Q5_4   0.04  0.01  0.12 -0.11  0.85 -0.12  0.05  0.02  0.01  0.06 0.73 0.272
Q5_5   0.11  0.03  0.06 -0.23  0.97 -0.15 -0.07  0.06 -0.02 -0.09 0.76 0.239
Q5_6   0.07  0.00  0.02  0.09  0.61 -0.01  0.30 -0.05 -0.11  0.00 0.73 0.274
Q5_7  -0.04  0.16  0.01  0.65  0.31 -0.23 -0.05 -0.04 -0.01 -0.06 0.60 0.399
Q5_8  -0.09 -0.01  0.04  0.27  0.61  0.00  0.15 -0.05 -0.02  0.00 0.67 0.333
Q5_9   0.07 -0.01 -0.22  0.51  0.37  0.14  0.11 -0.05 -0.03  0.05 0.72 0.281
Q5_10  0.09 -0.05  0.02  0.42  0.30  0.00  0.06 -0.16  0.01 -0.07 0.52 0.479
Q5_11  0.15  0.05 -0.07  0.13  0.21  0.26  0.09  0.23  0.02 -0.02 0.56 0.437
Q5_12 -0.06  0.08  0.19  0.02  0.27  0.20  0.24 -0.01 -0.02  0.05 0.52 0.478
Q6_1  -0.03  0.80 -0.24 -0.02 -0.03  0.15  0.14  0.18  0.10  0.03 0.78 0.222
Q6_2  -0.06  0.97 -0.02 -0.14  0.05  0.06  0.06  0.06  0.02  0.12 0.85 0.154
Q6_3   0.00  0.92  0.00  0.02  0.14 -0.10 -0.11  0.00  0.07  0.06 0.82 0.181
Q6_4  -0.04  0.94  0.07 -0.16  0.01 -0.04  0.11 -0.07 -0.06  0.03 0.74 0.256
Q6_5   0.01  0.19 -0.15  0.34  0.08  0.19 -0.20  0.21  0.16 -0.10 0.43 0.575
Q6_6   0.00  0.52  0.03  0.34 -0.05  0.18 -0.14 -0.14  0.09 -0.03 0.79 0.214
Q6_7   0.11  0.55  0.02  0.43 -0.10 -0.03 -0.09 -0.05  0.04 -0.04 0.80 0.197
Q6_8  -0.06  0.60  0.04  0.40 -0.15  0.08 -0.03 -0.08 -0.02 -0.05 0.78 0.216
Q6_9  -0.05 -0.08  0.09  0.79 -0.21 -0.08 -0.01  0.30  0.12 -0.01 0.57 0.431
Q6_10 -0.03 -0.05 -0.05  0.74 -0.10  0.15  0.03  0.18 -0.12  0.14 0.52 0.478
Q6_11 -0.05  0.06  0.19  0.69 -0.04  0.06 -0.01  0.04  0.01  0.28 0.70 0.298
Q7_1  -0.02  0.12  0.07  0.07  0.11  0.58  0.04  0.06  0.08  0.02 0.75 0.251
Q7_2   0.02  0.06  0.41  0.11  0.15  0.21 -0.11 -0.02  0.09 -0.04 0.61 0.389
Q7_3  -0.10  0.04  0.89  0.00  0.11 -0.14 -0.07  0.13  0.06  0.16 0.72 0.282
Q7_4  -0.10  0.07  0.68 -0.09 -0.07  0.46 -0.04 -0.15 -0.10  0.08 0.68 0.324
Q7_5   0.05 -0.04  0.57  0.12 -0.12  0.29  0.03  0.05 -0.04 -0.01 0.71 0.291
Q7_6   0.03  0.12  0.58  0.01 -0.02  0.02  0.09  0.13  0.07 -0.05 0.62 0.376
Q7_7   0.02 -0.14  0.84 -0.03  0.10 -0.13  0.07  0.24  0.07  0.12 0.79 0.205
Q7_8   0.02 -0.14  0.54  0.17  0.00  0.18 -0.02  0.02 -0.03 -0.18 0.63 0.367
Q7_9   0.09  0.02  0.05 -0.08 -0.05  0.76  0.15  0.04 -0.05  0.01 0.73 0.274
Q7_10  0.19  0.07  0.07 -0.13 -0.07  0.79  0.04 -0.08  0.00  0.03 0.78 0.216
Q7_11  0.24  0.02  0.28  0.00  0.07  0.38 -0.14  0.11 -0.19 -0.30 0.77 0.229
Q7_12  0.01  0.03  0.22  0.13  0.09  0.07 -0.07  0.59  0.03 -0.15 0.67 0.327
Q7_13 -0.07  0.00  0.22  0.22 -0.08 -0.06 -0.07  0.69 -0.05  0.07 0.58 0.422
Q7_14 -0.04 -0.06  0.55  0.05  0.13 -0.07 -0.01  0.33 -0.10  0.18 0.52 0.478
Q7_15  0.12 -0.03  0.01  0.10 -0.10  0.75  0.03 -0.02 -0.06  0.14 0.67 0.330
      com
Q4_1  1.3
Q4_2  1.3
Q4_3  1.2
Q4_4  1.3
Q4_5  2.3
Q4_6  2.6
Q4_7  3.7
Q4_8  1.1
Q4_9  2.7
Q4_10 1.4
Q4_11 1.3
Q4_12 3.8
Q4_13 1.7
Q4_14 3.7
Q4_15 1.9
Q4_16 2.7
Q4_17 1.4
Q4_18 1.2
Q4_19 1.8
Q5_1  5.9
Q5_2  3.0
Q5_3  2.4
Q5_4  1.1
Q5_5  1.2
Q5_6  1.6
Q5_7  1.9
Q5_8  1.6
Q5_9  2.7
Q5_10 2.4
Q5_11 4.7
Q5_12 4.1
Q6_1  1.5
Q6_2  1.1
Q6_3  1.1
Q6_4  1.1
Q6_5  5.5
Q6_6  2.5
Q6_7  2.2
Q6_8  2.1
Q6_9  1.6
Q6_10 1.4
Q6_11 1.5
Q7_1  1.3
Q7_2  2.4
Q7_3  1.2
Q7_4  2.1
Q7_5  1.8
Q7_6  1.3
Q7_7  1.4
Q7_8  1.9
Q7_9  1.2
Q7_10 1.3
Q7_11 5.0
Q7_12 1.7
Q7_13 1.6
Q7_14 2.2
Q7_15 1.2

                       PA3  PA2  PA6 PA10  PA4  PA5  PA9  PA7  PA1  PA8
SS loadings           9.78 5.08 5.07 4.95 4.15 4.30 2.11 1.69 1.50 0.71
Proportion Var        0.17 0.09 0.09 0.09 0.07 0.08 0.04 0.03 0.03 0.01
Cumulative Var        0.17 0.26 0.35 0.44 0.51 0.58 0.62 0.65 0.68 0.69
Proportion Explained  0.25 0.13 0.13 0.13 0.11 0.11 0.05 0.04 0.04 0.02
Cumulative Proportion 0.25 0.38 0.51 0.63 0.74 0.85 0.90 0.94 0.98 1.00

 With factor correlations of 
       PA3   PA2   PA6  PA10  PA4   PA5   PA9   PA7  PA1   PA8
PA3   1.00  0.54  0.62  0.71 0.51  0.67  0.58  0.14 0.27 -0.21
PA2   0.54  1.00  0.43  0.67 0.36  0.57  0.44 -0.02 0.31 -0.16
PA6   0.62  0.43  1.00  0.68 0.55  0.59  0.42  0.24 0.14 -0.18
PA10  0.71  0.67  0.68  1.00 0.55  0.73  0.57  0.10 0.34 -0.22
PA4   0.51  0.36  0.55  0.55 1.00  0.58  0.36  0.19 0.15  0.07
PA5   0.67  0.57  0.59  0.73 0.58  1.00  0.44  0.18 0.30 -0.16
PA9   0.58  0.44  0.42  0.57 0.36  0.44  1.00  0.16 0.21 -0.25
PA7   0.14 -0.02  0.24  0.10 0.19  0.18  0.16  1.00 0.02  0.03
PA1   0.27  0.31  0.14  0.34 0.15  0.30  0.21  0.02 1.00  0.07
PA8  -0.21 -0.16 -0.18 -0.22 0.07 -0.16 -0.25  0.03 0.07  1.00

Mean item complexity =  2.1
Test of the hypothesis that 10 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  84.54
The degrees of freedom for the model are 1071  and the objective function was  35.1 

The root mean square of the residuals (RMSR) is  0.03 
The df corrected root mean square of the residuals is  0.03 

Fit based upon off diagonal values = 1

print(fit$loadings, cutoff=0.3)

Loadings:
      PA3    PA2    PA6    PA10   PA4    PA5    PA9    PA7    PA1    PA8   
Q4_1   0.961                                                               
Q4_2   0.840                                                               
Q4_3   0.987                                                               
Q4_4   0.892                                                               
Q4_5   0.502                                                               
Q4_6   0.326                                                          0.522
Q4_7                 0.361                                            0.420
Q4_8   0.855                                                               
Q4_9   0.619               -0.340                                          
Q4_10  0.844                                                               
Q4_11  0.640                                                               
Q4_12                                                          0.470       
Q4_13  0.334                                                   0.688       
Q4_14  0.373                0.365                                          
Q4_15  0.627                                                               
Q4_16  0.619                                     0.313                     
Q4_17  0.630                                                               
Q4_18  0.863                                                               
Q4_19  0.569                                                               
Q5_1                                                                       
Q5_2                               0.349         0.537                     
Q5_3                               0.441         0.596                     
Q5_4                               0.850                                   
Q5_5                               0.973                                   
Q5_6                               0.610         0.301                     
Q5_7                        0.655  0.309                                   
Q5_8                               0.612                                   
Q5_9                        0.513  0.372                                   
Q5_10                       0.419                                          
Q5_11                                                                      
Q5_12                                                                      
Q6_1          0.805                                                        
Q6_2          0.970                                                        
Q6_3          0.918                                                        
Q6_4          0.937                                                        
Q6_5                        0.338                                          
Q6_6          0.518         0.336                                          
Q6_7          0.550         0.428                                          
Q6_8          0.595         0.402                                          
Q6_9                        0.791                                          
Q6_10                       0.742                                          
Q6_11                       0.692                                          
Q7_1                                      0.581                            
Q7_2                 0.412                                                 
Q7_3                 0.885                                                 
Q7_4                 0.682                0.464                            
Q7_5                 0.573                                                 
Q7_6                 0.580                                                 
Q7_7                 0.835                                                 
Q7_8                 0.544                                                 
Q7_9                                      0.763                            
Q7_10                                     0.795                            
Q7_11                                     0.375                      -0.302
Q7_12                                                   0.590              
Q7_13                                                   0.691              
Q7_14                0.549                              0.326              
Q7_15                                     0.746                            

                 PA3   PA2   PA6  PA10   PA4   PA5   PA9   PA7   PA1   PA8
SS loadings    8.886 4.587 4.346 4.158 3.566 3.442 1.599 1.515 1.205 1.076
Proportion Var 0.156 0.080 0.076 0.073 0.063 0.060 0.028 0.027 0.021 0.019
Cumulative Var 0.156 0.236 0.313 0.386 0.448 0.509 0.537 0.563 0.584 0.603

fit <- psych::fa(r = cov.dat, nfactors = 10, rotate = "Promax", fm = "pa", covar = T)
fit

Factor Analysis using method =  pa
Call: psych::fa(r = cov.dat, nfactors = 10, rotate = "Promax", covar = T, 
    fm = "pa")
Unstandardized loadings (pattern matrix) based upon covariance matrix
        PA1   PA9   PA2   PA3   PA6   PA4   PA5   PA7  PA10   PA8   h2   u2
Q4_1   0.73 -0.14 -0.14 -0.04  0.20  0.05 -0.10  0.05 -0.05  0.15 0.49 0.26
Q4_2   0.64 -0.10 -0.03 -0.11  0.18  0.08 -0.04 -0.02  0.16  0.11 0.46 0.22
Q4_3   0.74 -0.18 -0.08 -0.01  0.12  0.09 -0.12  0.08 -0.06  0.05 0.45 0.25
Q4_4   0.61 -0.07  0.12 -0.05  0.11  0.10 -0.23 -0.06 -0.03  0.11 0.46 0.21
Q4_5   0.42  0.00 -0.02 -0.04  0.24  0.04  0.07 -0.07  0.20  0.15 0.45 0.33
Q4_6   0.25 -0.03  0.14  0.12  0.16 -0.06  0.11  0.05 -0.06  0.47 0.59 0.37
Q4_7   0.14  0.09  0.36  0.07 -0.12  0.00  0.00 -0.02 -0.10  0.34 0.41 0.47
Q4_8   0.79 -0.03 -0.04  0.02 -0.01  0.00 -0.04 -0.05  0.14  0.02 0.53 0.33
Q4_9   0.77 -0.27  0.21  0.06 -0.04 -0.04  0.14  0.02  0.16 -0.19 0.59 0.42
Q4_10  0.58  0.06  0.12  0.01 -0.07  0.08 -0.24 -0.02 -0.03  0.10 0.37 0.25
Q4_11  0.65  0.21  0.03 -0.02 -0.04 -0.05 -0.03  0.04  0.05  0.03 0.56 0.35
Q4_12  0.39  0.30  0.19  0.13 -0.16 -0.03  0.13 -0.08  0.52  0.01 0.74 0.37
Q4_13  0.37  0.07 -0.06  0.10  0.03  0.09  0.17 -0.01  0.52 -0.10 0.53 0.23
Q4_14  0.44  0.36 -0.05  0.04 -0.11 -0.10  0.12  0.13  0.04  0.05 0.45 0.35
Q4_15  0.69  0.26 -0.14  0.00 -0.12 -0.04  0.07  0.02 -0.04 -0.06 0.57 0.27
Q4_16  0.69  0.08 -0.21  0.17 -0.15 -0.05  0.12  0.01 -0.21  0.08 0.57 0.32
Q4_17  0.69  0.05  0.05  0.07 -0.05 -0.13  0.00 -0.05  0.04 -0.01 0.48 0.45
Q4_18  0.70  0.07 -0.04 -0.12  0.04  0.05 -0.04 -0.09  0.12  0.06 0.50 0.17
Q4_19  0.70 -0.04  0.18  0.00 -0.05 -0.08  0.18 -0.02  0.12 -0.08 0.63 0.31
Q5_1   0.19  0.16 -0.06 -0.16  0.23  0.06  0.35  0.05  0.06 -0.03 0.46 0.44
Q5_2  -0.02 -0.09  0.21  0.05  0.07  0.10  0.61 -0.07  0.08  0.16 0.66 0.41
Q5_3   0.03  0.02 -0.12 -0.05  0.18  0.14  0.77 -0.01  0.13  0.03 0.78 0.31
Q5_4  -0.02 -0.13  0.13  0.02 -0.10  0.94  0.10  0.00  0.05  0.04 0.87 0.36
Q5_5   0.02 -0.21  0.05  0.02 -0.12  1.10 -0.04  0.03  0.00 -0.12 0.85 0.22
Q5_6   0.09  0.10  0.01  0.00 -0.02  0.37  0.27 -0.05 -0.10 -0.02 0.55 0.27
Q5_7  -0.01  0.66  0.00  0.11 -0.21  0.20 -0.05 -0.07 -0.02 -0.05 0.49 0.39
Q5_8  -0.08  0.28  0.04 -0.02  0.04  0.42  0.25 -0.07 -0.04  0.02 0.68 0.44
Q5_9   0.06  0.49 -0.20 -0.02  0.18  0.14  0.18 -0.05 -0.07  0.08 0.65 0.34
Q5_10  0.10  0.31  0.03 -0.04  0.00  0.11  0.08 -0.14 -0.03 -0.01 0.31 0.39
Q5_11  0.16  0.12 -0.07  0.04  0.30  0.07  0.14  0.21 -0.04  0.00 0.46 0.45
Q5_12  0.02  0.00  0.18  0.08  0.18  0.08  0.26  0.01 -0.05  0.05 0.44 0.47
Q6_1   0.01 -0.03 -0.17  0.66  0.09 -0.03  0.11  0.13  0.06  0.04 0.45 0.26
Q6_2  -0.03 -0.19 -0.01  0.90  0.06  0.00  0.04  0.07  0.00  0.11 0.65 0.18
Q6_3  -0.05 -0.03 -0.02  0.83 -0.05  0.14 -0.09  0.02  0.07  0.07 0.61 0.25
Q6_4   0.03 -0.23  0.06  0.87 -0.04 -0.02  0.04 -0.05 -0.05  0.01 0.58 0.28
Q6_5  -0.06  0.42 -0.15  0.13  0.25  0.17 -0.14  0.19  0.15 -0.08 0.39 0.68
Q6_6  -0.01  0.20  0.00  0.43  0.15  0.05 -0.13 -0.09  0.13 -0.04 0.45 0.22
Q6_7   0.11  0.33  0.01  0.47 -0.01 -0.05 -0.13 -0.05  0.06 -0.04 0.54 0.23
Q6_8  -0.01  0.32  0.01  0.52  0.08 -0.11 -0.10 -0.07  0.04 -0.06 0.57 0.25
Q6_9   0.03  1.05  0.10 -0.12 -0.11 -0.25 -0.02  0.33  0.16 -0.03 0.74 0.75
Q6_10 -0.03  0.64 -0.03 -0.04  0.12 -0.06 -0.06  0.14 -0.04  0.08 0.38 0.46
Q6_11 -0.09  0.64  0.22  0.04  0.03 -0.07 -0.01  0.01  0.07  0.24 0.61 0.33
Q7_1  -0.04  0.05  0.06  0.08  0.55  0.04  0.12  0.04  0.03  0.03 0.54 0.27
Q7_2  -0.01  0.12  0.33  0.01  0.21  0.15 -0.05 -0.05  0.06 -0.05 0.41 0.33
Q7_3  -0.09  0.03  0.86  0.03 -0.12  0.10 -0.04  0.10  0.06  0.14 0.68 0.34
Q7_4  -0.10 -0.15  0.63  0.06  0.44 -0.12 -0.04 -0.16 -0.08  0.07 0.61 0.35
Q7_5   0.08  0.11  0.52 -0.05  0.28 -0.13 -0.02  0.01 -0.04 -0.02 0.60 0.30
Q7_6   0.10  0.11  0.51  0.08  0.01 -0.05  0.05  0.08  0.05 -0.05 0.49 0.36
Q7_7   0.06 -0.02  0.82 -0.09 -0.12  0.13  0.03  0.18  0.10  0.06 0.72 0.31
Q7_8   0.08  0.18  0.45 -0.11  0.14 -0.01 -0.06 -0.02 -0.02 -0.15 0.44 0.33
Q7_9   0.09 -0.12  0.03  0.00  0.78 -0.10  0.14  0.03 -0.06  0.01 0.65 0.34
Q7_10  0.14 -0.16  0.01  0.07  0.77 -0.06  0.03 -0.06  0.02  0.01 0.62 0.27
Q7_11  0.20 -0.06  0.21  0.02  0.33  0.10 -0.15  0.07 -0.19 -0.23 0.48 0.22
Q7_12  0.03  0.17  0.22  0.04  0.14  0.14 -0.04  0.49 -0.05 -0.11 0.60 0.45
Q7_13 -0.07  0.30  0.19  0.02 -0.06 -0.04 -0.03  0.66 -0.06  0.08 0.53 0.45
Q7_14 -0.06  0.04  0.54 -0.01 -0.08  0.10  0.01  0.28 -0.07  0.19 0.47 0.50
Q7_15  0.06  0.01  0.00 -0.03  0.68 -0.11  0.05 -0.01 -0.04  0.11 0.48 0.34
        H2   U2
Q4_1  0.65 0.35
Q4_2  0.68 0.32
Q4_3  0.64 0.36
Q4_4  0.69 0.31
Q4_5  0.58 0.42
Q4_6  0.61 0.39
Q4_7  0.46 0.54
Q4_8  0.61 0.39
Q4_9  0.59 0.41
Q4_10 0.60 0.40
Q4_11 0.61 0.39
Q4_12 0.67 0.33
Q4_13 0.70 0.30
Q4_14 0.56 0.44
Q4_15 0.68 0.32
Q4_16 0.64 0.36
Q4_17 0.52 0.48
Q4_18 0.74 0.26
Q4_19 0.67 0.33
Q5_1  0.51 0.49
Q5_2  0.62 0.38
Q5_3  0.72 0.28
Q5_4  0.71 0.29
Q5_5  0.79 0.21
Q5_6  0.67 0.33
Q5_7  0.56 0.44
Q5_8  0.61 0.39
Q5_9  0.65 0.35
Q5_10 0.45 0.55
Q5_11 0.51 0.49
Q5_12 0.49 0.51
Q6_1  0.63 0.37
Q6_2  0.78 0.22
Q6_3  0.71 0.29
Q6_4  0.67 0.33
Q6_5  0.36 0.64
Q6_6  0.67 0.33
Q6_7  0.70 0.30
Q6_8  0.70 0.30
Q6_9  0.50 0.50
Q6_10 0.45 0.55
Q6_11 0.65 0.35
Q7_1  0.67 0.33
Q7_2  0.56 0.44
Q7_3  0.66 0.34
Q7_4  0.63 0.37
Q7_5  0.67 0.33
Q7_6  0.58 0.42
Q7_7  0.70 0.30
Q7_8  0.58 0.42
Q7_9  0.66 0.34
Q7_10 0.70 0.30
Q7_11 0.69 0.31
Q7_12 0.57 0.43
Q7_13 0.54 0.46
Q7_14 0.49 0.51
Q7_15 0.59 0.41

                       PA1  PA9  PA2  PA3  PA6  PA4  PA5  PA7 PA10  PA8
SS loadings           7.80 4.05 4.28 3.72 3.71 2.91 2.21 1.13 0.63 0.85
Proportion Var        0.15 0.08 0.08 0.07 0.07 0.06 0.04 0.02 0.01 0.02
Cumulative Var        0.15 0.23 0.32 0.39 0.46 0.52 0.57 0.59 0.60 0.62
Proportion Explained  0.25 0.13 0.14 0.12 0.12 0.09 0.07 0.04 0.02 0.03
Cumulative Proportion 0.25 0.38 0.52 0.63 0.75 0.85 0.92 0.95 0.97 1.00

 Standardized loadings (pattern matrix)
      item   PA1   PA9   PA2   PA3   PA6   PA4   PA5   PA7  PA10   PA8   h2
Q4_1     1  0.84 -0.16 -0.17 -0.05  0.23  0.05 -0.12  0.06 -0.05  0.17 0.65
Q4_2     2  0.78 -0.12 -0.04 -0.13  0.22  0.10 -0.04 -0.02  0.19  0.13 0.68
Q4_3     3  0.88 -0.21 -0.10 -0.02  0.15  0.11 -0.14  0.09 -0.07  0.05 0.64
Q4_4     4  0.75 -0.09  0.15 -0.06  0.13  0.12 -0.28 -0.08 -0.04  0.14 0.69
Q4_5     5  0.48  0.00 -0.02 -0.05  0.27  0.05  0.08 -0.08  0.22  0.17 0.58
Q4_6     6  0.25 -0.03  0.14  0.13  0.16 -0.06  0.11  0.05 -0.06  0.48 0.61
Q4_7     7  0.15  0.10  0.39  0.08 -0.13  0.00  0.00 -0.02 -0.11  0.37 0.46
Q4_8     8  0.85 -0.03 -0.05  0.02 -0.01  0.00 -0.04 -0.05  0.15  0.02 0.61
Q4_9     9  0.76 -0.27  0.21  0.06 -0.04 -0.04  0.14  0.02  0.16 -0.19 0.59
Q4_10   10  0.73  0.08  0.15  0.01 -0.09  0.10 -0.31 -0.03 -0.04  0.12 0.60
Q4_11   11  0.68  0.22  0.03 -0.02 -0.04 -0.05 -0.03  0.04  0.05  0.04 0.61
Q4_12   12  0.37  0.28  0.19  0.12 -0.15 -0.03  0.12 -0.08  0.49  0.01 0.67
Q4_13   13  0.42  0.08 -0.06  0.11  0.03  0.11  0.19 -0.01  0.60 -0.12 0.70
Q4_14   14  0.49  0.40 -0.05  0.04 -0.12 -0.11  0.13  0.15  0.04  0.06 0.56
Q4_15   15  0.76  0.28 -0.16  0.00 -0.14 -0.04  0.08  0.02 -0.04 -0.06 0.68
Q4_16   16  0.73  0.09 -0.22  0.18 -0.16 -0.06  0.13  0.01 -0.22  0.08 0.64
Q4_17   17  0.71  0.05  0.05  0.07 -0.05 -0.14  0.00 -0.06  0.05 -0.01 0.52
Q4_18   18  0.85  0.09 -0.04 -0.14  0.05  0.06 -0.05 -0.10  0.15  0.07 0.74
Q4_19   19  0.72 -0.04  0.19  0.00 -0.05 -0.08  0.18 -0.03  0.13 -0.08 0.67
Q5_1    20  0.20  0.17 -0.06 -0.17  0.24  0.06  0.37  0.05  0.06 -0.04 0.51
Q5_2    21 -0.02 -0.09  0.21  0.05  0.07  0.10  0.59 -0.07  0.08  0.16 0.62
Q5_3    22  0.03  0.02 -0.11 -0.05  0.17  0.13  0.73 -0.01  0.12  0.03 0.72
Q5_4    23 -0.02 -0.12  0.12  0.02 -0.09  0.85  0.09  0.00  0.05  0.04 0.71
Q5_5    24  0.02 -0.20  0.05  0.02 -0.12  1.06 -0.04  0.02  0.00 -0.11 0.79
Q5_6    25  0.10  0.11  0.01  0.00 -0.02  0.41  0.29 -0.06 -0.11 -0.02 0.67
Q5_7    26 -0.01  0.70  0.00  0.12 -0.22  0.22 -0.05 -0.07 -0.02 -0.05 0.56
Q5_8    27 -0.08  0.26  0.04 -0.02  0.03  0.40  0.23 -0.07 -0.03  0.01 0.61
Q5_9    28  0.06  0.49 -0.20 -0.02  0.18  0.14  0.18 -0.06 -0.07  0.08 0.65
Q5_10   29  0.11  0.38  0.04 -0.05  0.00  0.13  0.10 -0.16 -0.04 -0.02 0.45
Q5_11   30  0.17  0.12 -0.08  0.05  0.32  0.07  0.15  0.22 -0.05  0.00 0.51
Q5_12   31  0.02  0.00  0.19  0.09  0.19  0.08  0.28  0.01 -0.05  0.05 0.49
Q6_1    32  0.01 -0.04 -0.20  0.78  0.11 -0.04  0.13  0.16  0.07  0.05 0.63
Q6_2    33 -0.04 -0.20 -0.01  0.98  0.06  0.00  0.05  0.07  0.01  0.12 0.78
Q6_3    34 -0.05 -0.03 -0.02  0.90 -0.06  0.15 -0.09  0.02  0.07  0.08 0.71
Q6_4    35  0.03 -0.25  0.06  0.94 -0.05 -0.03  0.04 -0.05 -0.05  0.01 0.67
Q6_5    36 -0.06  0.40 -0.14  0.12  0.24  0.16 -0.14  0.18  0.15 -0.07 0.36
Q6_6    37 -0.01  0.24  0.01  0.53  0.18  0.06 -0.15 -0.11  0.16 -0.05 0.67
Q6_7    38  0.12  0.38  0.01  0.54 -0.01 -0.06 -0.15 -0.06  0.07 -0.05 0.70
Q6_8    39 -0.01  0.35  0.01  0.58  0.09 -0.12 -0.11 -0.08  0.05 -0.07 0.70
Q6_9    40  0.02  0.86  0.08 -0.10 -0.09 -0.20 -0.01  0.27  0.13 -0.03 0.50
Q6_10   41 -0.03  0.70 -0.03 -0.04  0.13 -0.07 -0.07  0.15 -0.04  0.08 0.45
Q6_11   42 -0.09  0.66  0.23  0.04  0.03 -0.07 -0.01  0.01  0.07  0.24 0.65
Q7_1    43 -0.05  0.06  0.06  0.09  0.61  0.04  0.13  0.04  0.03  0.03 0.67
Q7_2    44 -0.01  0.14  0.39  0.02  0.24  0.17 -0.06 -0.05  0.07 -0.05 0.56
Q7_3    45 -0.09  0.03  0.85  0.03 -0.12  0.10 -0.04  0.09  0.06  0.14 0.66
Q7_4    46 -0.10 -0.15  0.65  0.07  0.45 -0.12 -0.04 -0.16 -0.08  0.07 0.63
Q7_5    47  0.09  0.12  0.55 -0.05  0.30 -0.14 -0.02  0.02 -0.04 -0.02 0.67
Q7_6    48  0.11  0.12  0.55  0.09  0.01 -0.06  0.05  0.09  0.05 -0.06 0.58
Q7_7    49  0.06 -0.02  0.81 -0.09 -0.12  0.13  0.03  0.17  0.10  0.06 0.70
Q7_8    50  0.09  0.20  0.51 -0.13  0.16 -0.01 -0.07 -0.02 -0.02 -0.17 0.58
Q7_9    51  0.09 -0.12  0.03  0.00  0.79 -0.10  0.14  0.03 -0.06  0.01 0.66
Q7_10   52  0.15 -0.17  0.01  0.08  0.82 -0.07  0.03 -0.06  0.02  0.01 0.70
Q7_11   53  0.24 -0.07  0.25  0.03  0.40  0.11 -0.18  0.08 -0.22 -0.27 0.69
Q7_12   54  0.02  0.17  0.22  0.04  0.14  0.13 -0.04  0.48 -0.05 -0.11 0.57
Q7_13   55 -0.07  0.30  0.19  0.02 -0.06 -0.04 -0.04  0.66 -0.06  0.09 0.54
Q7_14   56 -0.06  0.04  0.55 -0.02 -0.09  0.10  0.01  0.28 -0.07  0.19 0.49
Q7_15   57  0.06  0.01  0.00 -0.03  0.75 -0.12  0.05 -0.01 -0.05  0.12 0.59
        u2
Q4_1  0.35
Q4_2  0.32
Q4_3  0.36
Q4_4  0.31
Q4_5  0.42
Q4_6  0.39
Q4_7  0.54
Q4_8  0.39
Q4_9  0.41
Q4_10 0.40
Q4_11 0.39
Q4_12 0.33
Q4_13 0.30
Q4_14 0.44
Q4_15 0.32
Q4_16 0.36
Q4_17 0.48
Q4_18 0.26
Q4_19 0.33
Q5_1  0.49
Q5_2  0.38
Q5_3  0.28
Q5_4  0.29
Q5_5  0.21
Q5_6  0.33
Q5_7  0.44
Q5_8  0.39
Q5_9  0.35
Q5_10 0.55
Q5_11 0.49
Q5_12 0.51
Q6_1  0.37
Q6_2  0.22
Q6_3  0.29
Q6_4  0.33
Q6_5  0.64
Q6_6  0.33
Q6_7  0.30
Q6_8  0.30
Q6_9  0.50
Q6_10 0.55
Q6_11 0.35
Q7_1  0.33
Q7_2  0.44
Q7_3  0.34
Q7_4  0.37
Q7_5  0.33
Q7_6  0.42
Q7_7  0.30
Q7_8  0.42
Q7_9  0.34
Q7_10 0.30
Q7_11 0.31
Q7_12 0.43
Q7_13 0.46
Q7_14 0.51
Q7_15 0.41

                 PA1  PA9  PA2  PA3  PA6  PA4  PA5  PA7 PA10  PA8
SS loadings     8.76 4.55 4.81 4.18 4.17 3.26 2.48 1.27 0.71 0.95
Proportion Var  0.15 0.08 0.08 0.07 0.07 0.06 0.04 0.02 0.01 0.02
Cumulative Var  0.15 0.23 0.32 0.39 0.46 0.52 0.57 0.59 0.60 0.62
Cum. factor Var 0.25 0.38 0.52 0.63 0.75 0.85 0.92 0.95 0.97 1.00

 With factor correlations of 
       PA1   PA9   PA2   PA3   PA6   PA4   PA5   PA7  PA10   PA8
PA1   1.00  0.73  0.59  0.55  0.71  0.56  0.56 -0.05 -0.17  0.08
PA9   0.73  1.00  0.67  0.69  0.76  0.60  0.62 -0.12 -0.21  0.06
PA2   0.59  0.67  1.00  0.42  0.60  0.57  0.49  0.07 -0.32  0.02
PA3   0.55  0.69  0.42  1.00  0.60  0.39  0.45 -0.18 -0.05  0.02
PA6   0.71  0.76  0.60  0.60  1.00  0.57  0.48 -0.03 -0.15  0.07
PA4   0.56  0.60  0.57  0.39  0.57  1.00  0.59 -0.04 -0.37  0.26
PA5   0.56  0.62  0.49  0.45  0.48  0.59  1.00 -0.07 -0.31  0.06
PA7  -0.05 -0.12  0.07 -0.18 -0.03 -0.04 -0.07  1.00  0.07 -0.02
PA10 -0.17 -0.21 -0.32 -0.05 -0.15 -0.37 -0.31  0.07  1.00  0.03
PA8   0.08  0.06  0.02  0.02  0.07  0.26  0.06 -0.02  0.03  1.00

Mean item complexity =  1.9
Test of the hypothesis that 10 factors are sufficient.

The degrees of freedom for the null model are  1596  and the objective function was  46.33
The degrees of freedom for the model are 1071  and the objective function was  6.24 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.02 

Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   PA1  PA9  PA2  PA3  PA6  PA4
Correlation of (regression) scores with factors   0.98 0.96 0.96 0.97 0.96 0.96
Multiple R square of scores with factors          0.96 0.92 0.92 0.94 0.92 0.92
Minimum correlation of possible factor scores     0.92 0.85 0.84 0.88 0.84 0.83
                                                   PA5  PA7 PA10  PA8
Correlation of (regression) scores with factors   0.92 0.85 0.86 0.83
Multiple R square of scores with factors          0.85 0.72 0.74 0.69
Minimum correlation of possible factor scores     0.71 0.45 0.48 0.38

print(fit$loadings, cutoff=0.3)

Loadings:
      PA1    PA9    PA2    PA3    PA6    PA4    PA5    PA7    PA10   PA8   
Q4_1   0.730                                                               
Q4_2   0.643                                                               
Q4_3   0.737                                                               
Q4_4   0.609                                                               
Q4_5   0.420                                                               
Q4_6                                                                  0.470
Q4_7                 0.363                                            0.344
Q4_8   0.788                                                               
Q4_9   0.767                                                               
Q4_10  0.580                                                               
Q4_11  0.654                                                               
Q4_12  0.387                                                   0.519       
Q4_13  0.370                                                   0.525       
Q4_14  0.435  0.359                                                        
Q4_15  0.694                                                               
Q4_16  0.686                                                               
Q4_17  0.689                                                               
Q4_18  0.699                                                               
Q4_19  0.697                                                               
Q5_1                                             0.349                     
Q5_2                                             0.608                     
Q5_3                                             0.767                     
Q5_4                                      0.936                            
Q5_5                                      1.095                            
Q5_6                                      0.370                            
Q5_7          0.657                                                        
Q5_8                                      0.419                            
Q5_9          0.485                                                        
Q5_10         0.315                                                        
Q5_11                              0.304                                   
Q5_12                                                                      
Q6_1                        0.660                                          
Q6_2                        0.895                                          
Q6_3                        0.832                                          
Q6_4                        0.869                                          
Q6_5          0.418                                                        
Q6_6                        0.434                                          
Q6_7          0.333         0.471                                          
Q6_8          0.319         0.522                                          
Q6_9          1.051                                     0.326              
Q6_10         0.643                                                        
Q6_11         0.641                                                        
Q7_1                               0.551                                   
Q7_2                 0.331                                                 
Q7_3                 0.861                                                 
Q7_4                 0.633         0.444                                   
Q7_5                 0.519                                                 
Q7_6                 0.510                                                 
Q7_7                 0.817                                                 
Q7_8                 0.446                                                 
Q7_9                               0.783                                   
Q7_10                              0.771                                   
Q7_11                              0.335                                   
Q7_12                                                   0.494              
Q7_13                                                   0.657              
Q7_14                0.541                                                 
Q7_15                              0.675                                   

                 PA1   PA9   PA2   PA3   PA6   PA4   PA5   PA7  PA10   PA8
SS loadings    7.214 4.173 3.751 3.625 3.218 2.886 1.809 1.188 0.971 0.809
Proportion Var 0.127 0.073 0.066 0.064 0.056 0.051 0.032 0.021 0.017 0.014
Cumulative Var 0.127 0.200 0.266 0.329 0.386 0.436 0.468 0.489 0.506 0.520

Selected Set of Items

We selected the following items based on these results:

Effective Learning (Q4)	Student Centered (Q5)	Interactive (Q6)	Engagement (Q7)
Q4-1	Q5-1	Q6-1	Q7-2
Q4-2	Q5-2	Q6-2	Q7-4
Q4-3	Q5-3	Q6-3	Q7-5
Q4-4	Q5-4	Q6-4	Q7-7
Q4-5	Q5-5	Q6-5	Q7-8
Q4-8	Q5-6	Q6-6	Q7-12
Q4-9	Q5-8	Q6-7	Q7-13
Q4-10	Q5-12	Q6-8	Q7-14
Q4-11		Q6-12
Q4-15
Q4-16
Q4-17
Q4-18
Q4-19

For the item stems, please see the document here.

Post EFA Item & Reliability Analysis

Effective Learning Items

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q4_",c(1:5,8:11, 15:19))])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q4_1	0.866	0.767	0.726	2.460	0.663	0.628
Q4_2	0.819	0.801	0.767	2.305	0.655	0.628
Q4_3	0.834	0.781	0.744	2.537	0.651	0.620
Q4_4	0.816	0.786	0.750	2.640	0.640	0.611
Q4_5	0.880	0.723	0.675	2.320	0.636	0.594
Q4_8	0.927	0.794	0.754	2.287	0.735	0.698
Q4_9	1.007	0.719	0.662	2.463	0.723	0.666
Q4_10	0.789	0.745	0.705	2.582	0.587	0.556
Q4_11	0.955	0.792	0.750	2.500	0.755	0.715
Q4_15	0.917	0.793	0.753	2.375	0.726	0.690
Q4_16	0.941	0.732	0.681	2.457	0.687	0.640
Q4_17	0.964	0.734	0.682	2.198	0.707	0.657
Q4_18	0.823	0.851	0.825	2.360	0.700	0.678
Q4_19	0.970	0.800	0.759	2.543	0.774	0.735

# post reliability
psych::alpha(dat[, paste0("Q4_",c(1:5,8:11, 15:19))])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q4_", c(1:5, 8:11, 15:19))])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.95      0.95    0.95      0.57  18 0.0043  2.4 0.69     0.56

 lower alpha upper     95% confidence boundaries
0.94 0.95 0.96 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
Q4_1       0.94      0.94    0.95      0.57  17   0.0046 0.0044  0.56
Q4_2       0.94      0.94    0.95      0.56  17   0.0047 0.0045  0.56
Q4_3       0.94      0.94    0.95      0.56  17   0.0046 0.0046  0.56
Q4_4       0.94      0.94    0.95      0.56  17   0.0047 0.0045  0.56
Q4_5       0.94      0.95    0.95      0.57  17   0.0045 0.0045  0.57
Q4_8       0.94      0.94    0.95      0.56  17   0.0047 0.0050  0.55
Q4_9       0.95      0.95    0.95      0.58  18   0.0045 0.0039  0.57
Q4_10      0.94      0.94    0.95      0.57  17   0.0046 0.0048  0.56
Q4_11      0.94      0.94    0.95      0.56  17   0.0047 0.0050  0.55
Q4_15      0.94      0.94    0.95      0.56  17   0.0047 0.0049  0.56
Q4_16      0.94      0.95    0.95      0.57  17   0.0045 0.0043  0.57
Q4_17      0.94      0.95    0.95      0.57  17   0.0045 0.0047  0.57
Q4_18      0.94      0.94    0.95      0.56  16   0.0048 0.0041  0.55
Q4_19      0.94      0.94    0.95      0.56  17   0.0047 0.0047  0.56

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q4_1  328  0.77  0.77  0.75   0.73  2.5 0.87
Q4_2  328  0.80  0.81  0.79   0.77  2.3 0.82
Q4_3  328  0.78  0.79  0.77   0.74  2.5 0.83
Q4_4  328  0.79  0.79  0.78   0.75  2.6 0.82
Q4_5  328  0.72  0.73  0.70   0.68  2.3 0.88
Q4_8  328  0.79  0.79  0.77   0.75  2.3 0.93
Q4_9  328  0.72  0.71  0.69   0.66  2.5 1.01
Q4_10 328  0.75  0.75  0.73   0.71  2.6 0.79
Q4_11 328  0.79  0.79  0.77   0.75  2.5 0.95
Q4_15 328  0.79  0.79  0.77   0.75  2.4 0.92
Q4_16 328  0.73  0.73  0.71   0.68  2.5 0.94
Q4_17 328  0.73  0.73  0.70   0.68  2.2 0.96
Q4_18 328  0.85  0.85  0.85   0.82  2.4 0.82
Q4_19 328  0.80  0.79  0.78   0.76  2.5 0.97

Non missing response frequency for each item
         1    2    3    4    5 miss
Q4_1  0.13 0.38 0.39 0.09 0.01    0
Q4_2  0.15 0.47 0.32 0.05 0.01    0
Q4_3  0.10 0.37 0.44 0.08 0.02    0
Q4_4  0.09 0.28 0.54 0.08 0.02    0
Q4_5  0.16 0.47 0.28 0.08 0.01    0
Q4_8  0.20 0.43 0.28 0.07 0.02    0
Q4_9  0.15 0.42 0.27 0.12 0.04    0
Q4_10 0.09 0.30 0.54 0.04 0.02    0
Q4_11 0.16 0.34 0.38 0.10 0.02    0
Q4_15 0.16 0.41 0.33 0.07 0.02    0
Q4_16 0.17 0.33 0.40 0.08 0.02    0
Q4_17 0.26 0.39 0.25 0.08 0.02    0
Q4_18 0.13 0.47 0.34 0.06 0.01    0
Q4_19 0.14 0.35 0.39 0.08 0.04    0

Initial Student Centered Items

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q5_",c(1:6, 8, 12))])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q5_1	0.951	0.686	0.591	2.637	0.652	0.561
Q5_2	1.035	0.778	0.697	2.954	0.804	0.720
Q5_3	1.046	0.790	0.711	2.662	0.825	0.743
Q5_4	1.106	0.785	0.700	3.500	0.867	0.772
Q5_5	1.034	0.736	0.643	3.530	0.760	0.664
Q5_6	0.906	0.827	0.771	2.927	0.748	0.697
Q5_8	1.055	0.792	0.713	2.905	0.835	0.752
Q5_12	0.952	0.701	0.608	2.881	0.666	0.578

# post reliability
psych::alpha(dat[, paste0("Q5_",c(1:6, 8, 12))])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q5_", c(1:6, 8, 12))])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
       0.9       0.9     0.9      0.52 8.7 0.0087    3 0.77     0.51

 lower alpha upper     95% confidence boundaries
0.88 0.9 0.91 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
Q5_1       0.89      0.89    0.90      0.54 8.3   0.0093 0.0088  0.53
Q5_2       0.88      0.88    0.89      0.52 7.5   0.0100 0.0106  0.52
Q5_3       0.88      0.88    0.88      0.51 7.4   0.0101 0.0100  0.51
Q5_4       0.88      0.88    0.87      0.52 7.5   0.0100 0.0075  0.51
Q5_5       0.89      0.89    0.88      0.53 7.9   0.0095 0.0048  0.52
Q5_6       0.88      0.88    0.88      0.50 7.0   0.0105 0.0096  0.50
Q5_8       0.88      0.88    0.89      0.51 7.4   0.0102 0.0109  0.51
Q5_12      0.89      0.89    0.90      0.54 8.1   0.0094 0.0107  0.54

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q5_1  328  0.69  0.69  0.63   0.59  2.6 0.95
Q5_2  328  0.78  0.78  0.74   0.70  3.0 1.04
Q5_3  328  0.79  0.79  0.76   0.71  2.7 1.05
Q5_4  328  0.79  0.78  0.76   0.70  3.5 1.11
Q5_5  328  0.74  0.73  0.71   0.64  3.5 1.03
Q5_6  328  0.83  0.83  0.81   0.77  2.9 0.91
Q5_8  328  0.79  0.79  0.75   0.71  2.9 1.06
Q5_12 328  0.70  0.71  0.64   0.61  2.9 0.95

Non missing response frequency for each item
         1    2    3    4    5 miss
Q5_1  0.12 0.32 0.40 0.14 0.03    0
Q5_2  0.10 0.20 0.38 0.27 0.05    0
Q5_3  0.15 0.29 0.35 0.17 0.04    0
Q5_4  0.08 0.11 0.21 0.46 0.15    0
Q5_5  0.05 0.12 0.21 0.48 0.14    0
Q5_6  0.09 0.15 0.52 0.21 0.02    0
Q5_8  0.12 0.19 0.39 0.24 0.05    0
Q5_12 0.10 0.17 0.50 0.19 0.04    0

Interactive Items

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q6_",c(1:8, 11))])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q6_1	0.844	0.757	0.690	1.701	0.638	0.581
Q6_2	0.912	0.828	0.773	2.079	0.754	0.703
Q6_3	0.924	0.824	0.766	1.930	0.760	0.707
Q6_4	0.927	0.774	0.703	2.076	0.716	0.651
Q6_5	1.033	0.572	0.444	2.351	0.589	0.458
Q6_6	0.820	0.818	0.766	1.832	0.669	0.627
Q6_7	0.875	0.841	0.791	2.162	0.735	0.691
Q6_8	0.903	0.827	0.772	2.113	0.746	0.697
Q6_11	0.970	0.659	0.557	2.814	0.638	0.539

# post reliability
psych::alpha(dat[, paste0("Q6_",c(1:8, 11))])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q6_", c(1:8, 11))])

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean  sd median_r
      0.91      0.91    0.92      0.54  10 0.0076  2.1 0.7     0.57

 lower alpha upper     95% confidence boundaries
0.89 0.91 0.92 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r  S/N alpha se var.r med.r
Q6_1       0.90      0.90    0.91      0.54  9.3   0.0086 0.019  0.57
Q6_2       0.89      0.90    0.90      0.52  8.7   0.0091 0.018  0.56
Q6_3       0.89      0.90    0.90      0.52  8.7   0.0091 0.019  0.56
Q6_4       0.90      0.90    0.90      0.53  9.2   0.0087 0.017  0.56
Q6_5       0.92      0.92    0.92      0.59 11.4   0.0069 0.010  0.59
Q6_6       0.89      0.90    0.90      0.52  8.8   0.0090 0.021  0.56
Q6_7       0.89      0.90    0.90      0.52  8.6   0.0092 0.020  0.56
Q6_8       0.89      0.90    0.90      0.52  8.7   0.0091 0.020  0.56
Q6_11      0.91      0.91    0.92      0.56 10.4   0.0077 0.019  0.59

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q6_1  328  0.76  0.76  0.73   0.69  1.7 0.84
Q6_2  328  0.83  0.83  0.82   0.77  2.1 0.91
Q6_3  328  0.82  0.83  0.81   0.77  1.9 0.92
Q6_4  328  0.77  0.78  0.75   0.70  2.1 0.93
Q6_5  328  0.57  0.56  0.47   0.44  2.4 1.03
Q6_6  328  0.82  0.82  0.80   0.77  1.8 0.82
Q6_7  328  0.84  0.84  0.83   0.79  2.2 0.88
Q6_8  328  0.83  0.83  0.81   0.77  2.1 0.90
Q6_11 328  0.66  0.65  0.59   0.56  2.8 0.97

Non missing response frequency for each item
         1    2    3    4    5 miss
Q6_1  0.49 0.36 0.09 0.05 0.00    0
Q6_2  0.27 0.47 0.17 0.07 0.01    0
Q6_3  0.36 0.45 0.13 0.05 0.02    0
Q6_4  0.29 0.43 0.20 0.06 0.01    0
Q6_5  0.19 0.46 0.21 0.10 0.04    0
Q6_6  0.37 0.48 0.11 0.03 0.01    0
Q6_7  0.21 0.50 0.20 0.07 0.01    0
Q6_8  0.25 0.47 0.20 0.07 0.01    0
Q6_11 0.11 0.21 0.49 0.14 0.05    0

Engagement Items

# item analysis
fit <- psychometric::item.exam(dat[, paste0("Q7_",c(2, 4:5, 7:8, 12:14))])

kable(fit[,c(1:4,7:8)], format="html", digits=3) %>%
  kable_styling(full_width = T)%>%
  scroll_box(width="100%")

	Sample.SD	Item.total	Item.Tot.woi	Difficulty	Item.Reliab	Item.Rel.woi
Q7_2	0.857	0.701	0.607	2.692	0.599	0.519
Q7_4	0.980	0.710	0.602	2.841	0.694	0.589
Q7_5	0.948	0.798	0.720	2.875	0.756	0.682
Q7_7	1.014	0.789	0.701	3.652	0.799	0.710
Q7_8	0.877	0.736	0.648	2.814	0.644	0.567
Q7_12	1.023	0.717	0.605	3.390	0.732	0.618
Q7_13	0.989	0.571	0.430	3.579	0.564	0.425
Q7_14	0.986	0.694	0.581	3.610	0.684	0.573

# post reliability
psych::alpha(dat[, paste0("Q7_",c(2, 4:5, 7:8, 12:14))])

Reliability analysis   
Call: psych::alpha(x = dat[, paste0("Q7_", c(2, 4:5, 7:8, 12:14))])

  raw_alpha std.alpha G6(smc) average_r S/N   ase mean   sd median_r
      0.86      0.86    0.87      0.44 6.3 0.012  3.2 0.69     0.45

 lower alpha upper     95% confidence boundaries
0.84 0.86 0.88 

 Reliability if an item is dropped:
      raw_alpha std.alpha G6(smc) average_r S/N alpha se  var.r med.r
Q7_2       0.85      0.85    0.85      0.44 5.5    0.013 0.0148  0.45
Q7_4       0.85      0.85    0.84      0.44 5.5    0.013 0.0113  0.45
Q7_5       0.83      0.83    0.83      0.42 5.0    0.014 0.0124  0.42
Q7_7       0.83      0.84    0.84      0.42 5.1    0.014 0.0164  0.41
Q7_8       0.84      0.84    0.84      0.43 5.3    0.013 0.0146  0.45
Q7_12      0.85      0.85    0.85      0.44 5.6    0.013 0.0188  0.45
Q7_13      0.87      0.87    0.86      0.48 6.5    0.011 0.0083  0.47
Q7_14      0.85      0.85    0.85      0.45 5.7    0.013 0.0185  0.47

 Item statistics 
        n raw.r std.r r.cor r.drop mean   sd
Q7_2  328  0.70  0.71  0.66   0.61  2.7 0.86
Q7_4  328  0.71  0.71  0.68   0.60  2.8 0.98
Q7_5  328  0.80  0.80  0.79   0.72  2.9 0.95
Q7_7  328  0.79  0.78  0.75   0.70  3.7 1.01
Q7_8  328  0.74  0.75  0.70   0.65  2.8 0.88
Q7_12 328  0.72  0.71  0.65   0.61  3.4 1.02
Q7_13 328  0.57  0.56  0.47   0.43  3.6 0.99
Q7_14 328  0.69  0.69  0.62   0.58  3.6 0.99

Non missing response frequency for each item
         1    2    3    4    5 miss
Q7_2  0.11 0.21 0.57 0.09 0.02    0
Q7_4  0.10 0.21 0.47 0.17 0.05    0
Q7_5  0.10 0.18 0.51 0.17 0.04    0
Q7_7  0.05 0.09 0.17 0.53 0.16    0
Q7_8  0.10 0.17 0.55 0.15 0.02    0
Q7_12 0.07 0.09 0.32 0.43 0.10    0
Q7_13 0.02 0.11 0.32 0.36 0.19    0
Q7_14 0.05 0.08 0.24 0.48 0.15    0

Session information

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19042)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.1252 
[2] LC_CTYPE=English_United States.1252   
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.1252    

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] xtable_1.8-4      kableExtra_1.3.1  readxl_1.3.1      coda_0.19-4      
 [5] nFactors_2.4.1    lattice_0.20-41   psych_2.0.12      psychometric_2.2 
 [9] multilevel_2.6    MASS_7.3-53       nlme_3.1-151      mvtnorm_1.1-1    
[13] ggcorrplot_0.1.3  naniar_0.6.0      simsem_0.5-15     lslx_0.6.10      
[17] MIIVsem_0.5.5     lavaanPlot_0.5.1  semTools_0.5-4    lavaan_0.6-7     
[21] data.table_1.13.6 patchwork_1.1.1   forcats_0.5.0     stringr_1.4.0    
[25] dplyr_1.0.3       purrr_0.3.4       readr_1.4.0       tidyr_1.1.2      
[29] tibble_3.0.5      ggplot2_3.3.3     tidyverse_1.3.0  

loaded via a namespace (and not attached):
 [1] fs_1.5.0           lubridate_1.7.9.2  webshot_0.5.2      RColorBrewer_1.1-2
 [5] httr_1.4.2         rprojroot_2.0.2    tools_4.0.3        backports_1.2.0   
 [9] R6_2.5.0           DBI_1.1.1          colorspace_2.0-0   withr_2.4.0       
[13] tidyselect_1.1.0   mnormt_2.0.2       compiler_4.0.3     git2r_0.28.0      
[17] cli_2.2.0          rvest_0.3.6        xml2_1.3.2         scales_1.1.1      
[21] digest_0.6.27      pbivnorm_0.6.0     rmarkdown_2.6      pkgconfig_2.0.3   
[25] htmltools_0.5.1    highr_0.8          dbplyr_2.0.0       htmlwidgets_1.5.3 
[29] rlang_0.4.10       rstudioapi_0.13    visNetwork_2.0.9   generics_0.1.0    
[33] jsonlite_1.7.2     magrittr_2.0.1     Rcpp_1.0.6         munsell_0.5.0     
[37] fansi_0.4.2        lifecycle_0.2.0    visdat_0.5.3       stringi_1.5.3     
[41] whisker_0.4        yaml_2.2.1         grid_4.0.3         parallel_4.0.3    
[45] promises_1.1.1     crayon_1.3.4       haven_2.3.1        hms_1.0.0         
[49] tmvnsim_1.0-2      knitr_1.30         ps_1.5.0           pillar_1.4.7      
[53] stats4_4.0.3       reprex_0.3.0       glue_1.4.2         evaluate_0.14     
[57] modelr_0.1.8       vctrs_0.3.6        httpuv_1.5.5       cellranger_1.1.0  
[61] gtable_0.3.0       assertthat_0.2.1   xfun_0.20          broom_0.7.3       
[65] later_1.1.0.1      viridisLite_0.3.0  workflowr_1.6.2    DiagrammeR_1.0.6.1
[69] ellipsis_0.3.1