7 Canonical Bayesian Psychometric Modeling

This chapter provides an overview of the purposes that psychometric modeling serve and how a Bayesian approach can fit into this purpose. Other information was introduced such as directed acyclic graph (DAG) representations of basic models and notation for future chapters.

A canonical (conventional) psychometric analysis focuses on scoring and calibration.

• Scoring refers to arriving at a representation for an examinee based on their performance on an assessment, and
• Calibration refers to arriving at a representation for the measurement model parameters (and possibly hyper-parameters).

In a research or operational setting, these two core components can be the focus separately or together. When the focus is on the simultaneous assessment of measurement model parameters and person parameters, there may need to be concession made with how to conduct both. In one sense, we would like to estimate all the parameters simultaneous so that uncertainty in measurement model parameters is reflected in person parameter (ability) estimates. However, traditional psychometric analysis tends to proceed by 1) estimating the measurement model parameters only by first integrating the person parameter distribution out of the likelihood function, then 2) using the now estimated measurement model parameters as fixed quantities, we estimate the person parameters (factor scores). This process results in the uncertainty in the person parameters being decreased. One potential benefit of a Bayesian approach is that both calibration and scoring can be done simultaneously. This may not always be of interest in the current application so the traditional approach may still be done.

A canonical psychometric model can be expressed as a DAG using a model similar to the path models traditionally used in SEM. We expressed two forms of a model shown in the book below.

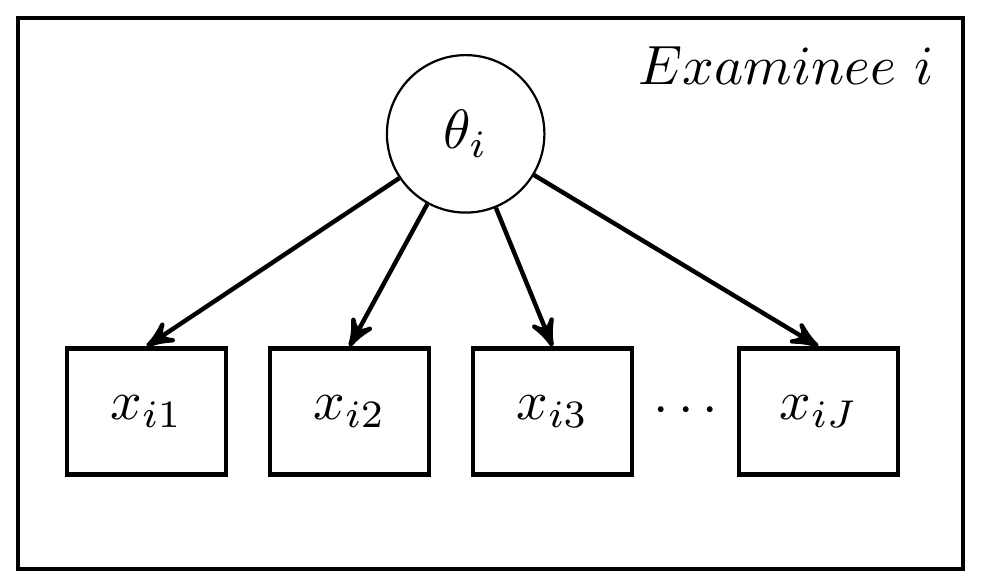
Figure 7.1: DAG for canonical psychometric modeling

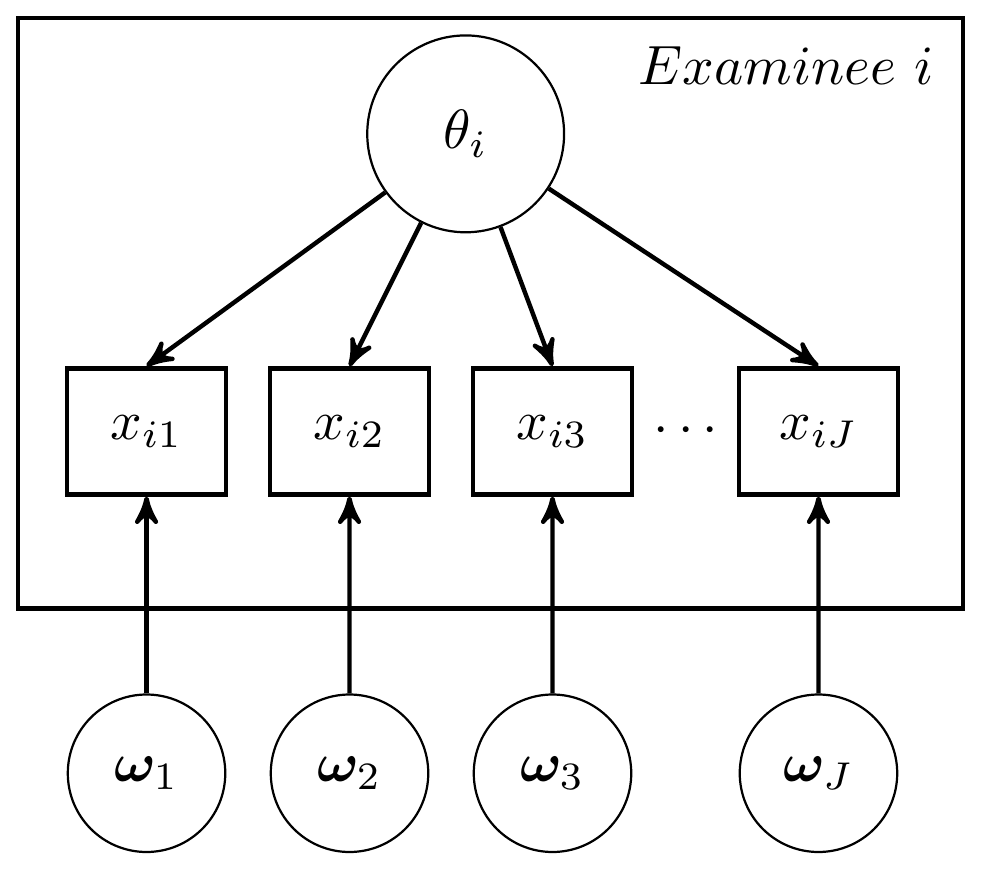
Figure 7.2: Expanded DAG to include measurement model parameters